Implementacja ultraszybkiego, zmiennoprzecinkowego FFT w FPGA

Aby móc dokonywać obliczeń na tak różnych zmiennych stosuje się zazwyczaj zmiennoprzecinkowy format zapisu liczb. Niestety ich przetwarzanie jest dużo mniej wydajne niż przeprowadzanie obliczeń na liczbach stałoprzecinkowych. Prowadzi to często do problemów, w sytuacji, gdy z jednej strony wymagany jest dynamiczny zakres zmiennych, a z drugiej duża szybkość pracy. Sytuacja taka ma miejsce również w algorytmach FFT (Fast Fourier Transform – szybka transformata Fouriera) stanowiących podstawę systemów DSP (Digital Signal Processing).

FFT podręcznikowo

Rys. 1. Przykład struktury motylkowej stosowanej w wyznaczaniu FFT

Podręczniki poświęcone implementacji FFT omawiają sposoby realizacji równoległego przetwarzania danych w dwunastu zmiennoprzecinkowych sumatorach i multiplikatorach. Przyspiesza to znacznie obliczenia, ale też prowadzi do szybkiego wyczerpania zasobów układu FPGA. Poniżej opisany zostanie alternatywny sposób realizacji FFT, który pozwala zachować krótki czas obliczeń i wykorzystać zalety formatu zmiennoprzecinkowego. Jest on oparty na hybrydowym połączeniu obliczeń zmienno- i stałoprzecinkowych, dzięki implementacji w pojedynczym układzie FPGA. Omawiany algorytm wykorzystuje wejścia i wyjścia w standardzie liczb zmiennoprzecinkowych IEEE pojedynczej precyzji. Pozwala to na zachowanie jednolitego standardu wymiany danych z innymi blokami funkcjonalnymi.

Algorytm

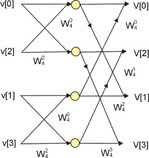
Implementacja FFT jest możliwa na wiele sposobów. Najpopularniejsze jest opracowanie Cooley-Turkey'a, które rekurencyjnie dzieli każdą N-punktową transformatę na parę N/2-punktowych transformat. Operacja ta jest powtarzana do momentu uzyskania serii dwupunktowych transformat, które wymagają tylko jednego, zespolonego mnożenia i dodawania. Następnie wykorzystywana jest tzw. struktura motylkowa (rys. 1) do obliczenia całej N-punktowej transformaty. Regularna budowa algorytmu i sekwencyjne wykonywanie obliczeń sprzyja jego programowej implementacji w procesorach DSP. Liczba wymaganych cykli maszynowych do wykonania mnożeń i dodawań zmiennoprzecinkowych jest ściśle powiązana z budową procesora. Rdzenie wyposażone w dedykowane bloki DSP pozwalają przeprowadzać takie obliczenia znacznie szybciej, co przekłada się na znacznie większą wydajność. Wadą jest sekwencyjność - wszystkie operacje matematyczne są wykonywane kolejno, jedna po drugiej, przez pojedynczą jednostkę obliczeniową.

Rys. 2. 16-punktowa FFT oparta o algorytm Winograd

Rys. 3. Łączenie bloków algorytmu Winograd pozwalające zwiększać liczbę wyznaczanych punktów

Inne sposoby optymalizacji FFT wykorzystują efektywnie zaprojektowaną część sprzętową. Algorytm Winograd został zaprojektowany pod kątem minimalizacji wymaganej liczby mnożeń i jest propozycją godną rozważenia w implementacjach sprzętowych. Do jego wad można zaliczyć dużą nieregularność adresowania poszczególnych próbek, która dyskwalifikuje go jako rozwiązanie stosowane w procesorach sygnałowych. Taka forma powoduje zbyt duże straty mocy obliczeniowej na wyznaczenie kolejnych adresów.

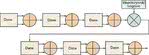
Problem nieregularnego adresowanie można rozwiązać skutecznie w układach FPGA wyposażonych w pamięć. Implementacja modułu wyznaczającego stosowne adresy znacznie przyspiesza obliczanie transformaty. Algorytm Winograd (16-punktowy) dekomponuje FFT na trzy grupy operacji dodawania/odejmowania po każdej ze stron układu mnożącego (rys. 2). Układ ten wykonuje 74 operacje dodawania oraz 18 operacji mnożenia dla każdej transformaty. Zmniejsza to liczbę potrzebnych operacji o dwie trzecie w stosunku do algorytmu Cooley-Turkey'a, który wymaga 176 dodawań i 72 mnożeń.

Bloki zmiennoprzecinkowe

Firma Andraka Consulting Group opracowała zoptymalizowane, zmiennoprzecinkowe bloki funkcjonalne do wyznaczania 4-, 8- oraz 16-punktowych FFT w oparciu o algorytm Winograd. Przeznaczone są ona dla układów FPGA z rodziny Virtex, które mają wbudowane moduły matematyczne - tzw. DSP48 slices. Ich wykorzystanie dodatkowo przyspiesza operacje. Możliwy jest wybór 1-, 4-, 8- i 16-punktowej transformaty. Maksymalna częstotliwość pracy układów FPGA jest ograniczona przez bloki DSP48 do 400MHz.

Rys. 4. Hybrydowy, zmiennoprzecinkowy 4, 8 i 16 punktowy moduł FFT

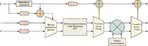
Obliczanie FFT oparte o algorytm Winograd jest uciążliwe dla transformat większych niż 16-punktowe. Powszechnie stosowanym rozwiązaniem jest pośrednie wyznaczanie transformaty w oparciu o moduły 4-, 8- i 16-punktowe. Metoda ta umieszcza dane w macierzy i wykonuje „mniejsze” FFT wzdłuż każdej kolumny, odwracając w fazie wynik i na końcu wykonuje dodatkowe przekształcenie wzdłuż każdego wiersza. Transformaty w zakresie od 32 do 2048 punktów obliczane są z wykorzystaniem transformat 32-, 64-, 128- lub 256-punktowych FFT, a te - przy użyciu modułów 4- 8- czy 16-punktowych. Ponowne użycie algorytmu pozwala uzyskać transformaty 512-, 1024-punktowe lub też 2048-punktowe, przy wykorzystaniu dodatkowej transformaty 8-punktowej (rys. 3). Opracowanie to można w prosty sposób przystosować do wyznaczania transformat 4096-punktowych przy użyciu dodatkowego modułu 16-punktowego. Na podobnej zasadzie możliwe jest dalsze zwiększanie liczby punktów.

Łączenie operacji zmienno- i stałoprzecinkowych

Tradycyjne implementacje systemu zmiennoprzecinkowego traktują każdą operację dodawania i mnożenia jako osobne działanie. Wymagają one dedykowanych wejść danych oraz wyjść dla wyniku. Wykonanie kilku takich podstawowych operacji pociąga za sobą konieczność przeprowadzenia normalizacji danych – zarówno wejściowych, jak i wyniku. Prowadzi to w prostej linii do znacznego oraz niepotrzebnego zużycia zasobów sprzętowych.

Godząc się na pewną niedokładność obliczeń, można operować na większych fragmentach algorytmu i traktować je jako blok stałoprzecinkowy, operujący na mantysie danych wejściowych. Denormalizacja przeprowadzana jest dopiero po kilku krokach algorytmu, a nie każdej elementarnej operacji. Dane wejściowe takiego bloku muszą zostać znormalizowane do postaci z ustalonym wykładnikiem i odpowiednio dużą liczbę bitów, która nie spowoduje przepełnienia dla żadnej kombinacji sygnałów wejściowych.

Wyznaczanie FFT oparte jest o algorytm Winograd, który oblicza transformaty 4-, 8- oraz 16-punktowe. Ciekawą własnością tej metody jest maksymalne zwiększenie amplitudy badanego sygnału 16 razy. Blok funkcjonalny jest idealnie przystosowany do pracy z liczbami stałoprzecinkowymi. Rysunek 4 pokazuje denormalizację zespolonego wejścia do „mniejszego” FFT. Największa, występująca próbka jest zapisana na 30-bitach z wyjustowaniem do lewej strony.

Pozostałe próbki są justowane do prawej strony. Wartość maksymalna jest wyznaczana dla każdej 4-, 8- czy 16-punktowej transformaty, więc obliczenia przeprowadzane są zawsze z największą, możliwą precyzją. Wewnątrz bloku FFT próbka rozszerzana jest do słowa 35-bitowego i w takiej formie kierowana jest na wyjście. Przepełnienie jest niemożliwe, bez względu na wartości podane na wejście. Każda zespolona para wyprowadzana z modułu FFT jest normalizowana i tworzone są zespolone komponenty I oraz Q z odgórnie określonym wykładnikiem. Największy komponent jest wyjustowany do lewej strony.

Podobnie jak w FFT wyznaczanym za pomocą liczb zmiennoprzecinkowych, tak i w omawianej technice nie dochodzi do utraty precyzji wyniku. Obliczenia są prowadzone na liczbach zmiennoprzecinkowych, obejmują kilka bloków funkcjonalnych i wszelkie przybliżenia odbywają się w ramach tego systemu liczbowego. Dopiero dane wychodzące z danego bloku ulegają przekształceniu na system stałoprzecinkowy, więc dokładność jest zawsze dopasowana do precyzji próbki o największej wartości.

Jak wspomniano wcześniej, do poprawnej pracy algorytmu potrzebny jest zmiana fazy sygnału. Jest ona realizowana przez zintegrowany z architekturą stałoprzecinkową moduł zespolonego mnożenia o rozmiarze 35x35 bitów. Wejście bloku FFT ma postać zespoloną. Dane przechowywane są jako para IQ ze znormalizowanym wykładnikiem. Największa próbka jest wyjustowana do lewej strony. Współczynnik obrotu jest dany jako 35-bitowa, stałoprzecinkowa para funkcji sinus oraz cosinus.

Wszystkie liczby mają ustalony wykładnik, a kąt obrotu ma ustaloną wartość, a więc wykładnik wyniku nie ulega zmianie. Może jednak zaistnieć sytuacja, w której obrót spowoduje przesunięcie wyniku o jeden bit. Normalizacja sprowadzi się wtedy do przesunięcie wyniku o ten jeden bit. Dane wejściowe i wyjściowe bloku FFT mają postać zmiennoprzecinkowej pary IQ zaokrąglonej do 30 bitów.

Dane zorganizowane w parę liczb zespolonych na etapie pośredniego przetwarzania sygnału, pozwalają na przechowywanie jedynie aktualnych wartości. Wejście i wyjście jest zgodne ze standardem IEEE pojedynczej precyzji, więc wymagana jest konwersja na wejściu i wyjściu układu FPGA.

Podsumowanie

Algorytm przedstawiony w artykule był implementowany w układzie Virtex-4 XC4VSX55-10 firmy Xilinx. Operacje matematyczne były przeprowadzane przy pomocy dedykowanych modułów matematycznych, wbudowanych w układ FPGA. Przyspieszyło to prowadzenie obliczeń, gdyż wyeliminowano tym sposobem relatywnie długie opóźnienia wprowadzanego przez łańcuchy przeniesień układu FPGA.

Opisana w niniejszym artykule metoda obliczania FFT pozwala wyznaczać transformaty z zakresu od 32 do 2048 punktów w układzie pracującym z zegarem do 400MHz. Zapewnia to wydajność na poziomie 400mln zespolonych próbek na sekundę i ogranicza zużycie zasobów sprzętowych wspomnianego układu FPGA do mniej niż 30%.

Rozbudowując powyższy algorytm o schemat przydzielania zasobów sprzętowych round-robin, obsługę interfejsu pamięci QDR dla danych wejściowych i wyjściowych oraz buforowanie wewnątrz urządzenia, możliwe jest uzyskanie przepustowości na poziomie 1,2mld próbek na sekundę.

Przyjmując za punkt odniesienia miarę „5N log N” stosowaną przy obliczaniu FFT na komputerze, jednowymiarowa FFT osiąga wydajność 22 gigaflopów na sekundę w każdym z trzech niezależnych modułów (równolegle), a całkowita wydajność kształtuje się na poziomi 66 gigaflopów na sekundę. Implementacja tego samego algorytmu na nowszych układach programowalnych pozwoliłaby na osiągnięcie jeszcze lepszych wyników.

Jakub Borzdyński