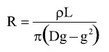Zliczanie kwadratów - sposób szybkiej oceny rezystancji ścieżek

Tabela 1. Rezystywność metali

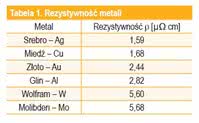
Koncepcja zasadza się na stwierdzeniu, że każdy dowolnego rozmiaru kwadrat, na jakie ścieżkę o stałej grubości można podzielić, ma tę samą rezystancję. Zależy ona jedynie od rezystywności materiału ścieżki i od jej grubości. Metodę tę można stosować do ścieżek wykonanych z dowolnego przewodnika. W tabeli 1 zestawiono rezystywności kilku najważniejszych metali.

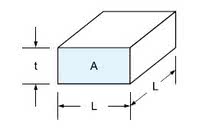
Podstawowym materiałem ścieżek na płytkach drukowanych jest miedź. Aluminium jest używane do metalizacji struktur półprzewodnikowych, do których metoda ta nadaje się również. Na rysunku 1 przedstawiono kwadrat miedzianej ścieżki, którego długość i szerokość oznaczono "L", grubość "g", a prąd płynie przez jego przekrój A = L·g. Rezystancja tego kwadratu wynosi zatem: R = ρ L/A = ρ/g.

Rys. 1. Rozmiary kwadratu miedzi

Rezystancja kwadratu, jak widać, jest ilorazem rezystywności przewodnika ρ i grubości ścieżki g i zupełnie nie zależy od jego rozmiaru. Zatem znajomość liczby kwadratów, na które można podzielić powierzchnię ścieżki, wystarczy do obliczenia jej rezystancji. Do liczby całkowitych kwadratów w ścieżce o stałej szerokości należy dodać pozostałą część w postaci ułamka.

Przykład
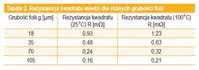
Do obliczeń trzeba znać rezystancję kwadratu. Układy elektroniczne są wykonywane na płytkach drukowanych o kilku standardowych grubościach folii miedzianej. Zależność rezystancji miedzianego kwadratu od grubości miedzianej folii przewodzącej w temperaturze 25°C i 100°C (termiczny współczynnik rezystancji miedzi wynosi 4,3·10-3/°C) jest przedstawiona w tabeli 2.

Rys. 2. Prostokątna miedziana ścieżka

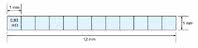
Na rysunku 2 pokazano prostokątną ścieżkę miedzianą o grubości 35 μm, o szerokości 1 mm i długości 12 mm. Można ją w wyobraźni podzielić na 12 kwadratów, z których każdy przy temperaturze 25°C, jak widać w tabeli, ma rezystancję 0,48 mΩ. Rezystancja ścieżki wynosi więc 5,8 mΩ.

Narożniki i złącza

Tabela 2. Rezystancja kwadratu miedzi dla różnych grubości folii

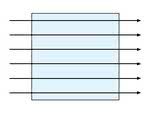
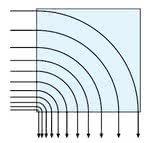
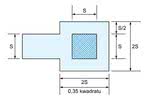
Powyższy przykład poprawnie przedstawia rezystancję ścieżki przy założeniu, że przez kwadrat prąd płynie strumieniem rozłożonym równomiernie, w sposób zilustrowany na rysunku 3a. Jednakże narożnik, jak przedstawia rysunek 3b, zmienia sposób przepływu prądu. W lewej dolnej części kwadratu prąd ma do przebycia krótszą drogę niż w prawej górnej. Wywołuje to tendencję do zwiększenia gęstości prądu w pobliżu wewnętrznego narożnika. Niejednorodność ta jest zilustrowana na rysunku 3b zagęszczeniem strzałek. Obliczono, że rezultatem tego efektu jest 0,56-krotne zmniejszenie równoważnej rezystancji narożnikowego kwadratu S · S (rys. 4).

Rys. 3a. Równomierny przepływ prądu przez kwadrat

Rys. 3b. Przepływ prądu przez kwadrat narożnikowy

Rys. 4. Równoważnik kwadratu narożnikowego = 0,56 kwadratu

W analogiczny sposób należy dokonywać poprawek w miejscach, w których do ścieżki na płytce są przylutowane złącza. Przyjmuje się w takich przypadkach, że rezystancja złącza jest pomijalna w stosunku do rezystancji ścieżki. Jeśli złącze zajmuje znaczną część miedzianego kwadratu, to jego rezystancja powinna zostać proporcjonalnie zmniejszona.

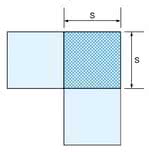
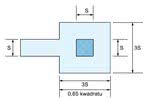
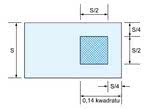
Niektóre konfiguracje szpilek złącza i równoważne dla nich rozmiary kwadratów są pokazane na rysunkach 5, 6 i 7. Zakratkowane pola oznaczają szpilki złącza w ścieżce.

Rys. 5. Równoważnik 3-krotnie rozszerzonego kwadratu ze stykiem złącza = 0,65 kwadratu

Rys. 6. Równoważnik 2-krotnie rozszerzonego kwadratu ze stykiem złącza = 0,35 kwadratu

Rys. 7. Równoważnik nierozszerzonego kwadratu ze stykiem złącza = 0,14 kwadratu

Przykład bardziej złożony

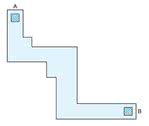
Na rysunku 8a pokazano przykład ścieżki o bardziej skomplikowanym kształcie, wymagającym więcej zabiegów przy obliczeniu. Przyjęto, że ścieżka o grubości 35 μm przewodzi w temperaturze 25°C przez całą długość, od punktu A do punktu B.

Rys. 8a. Przykład ścieżki o skomplikowanym przelotki kształcie ze stykami złącza

Rys. 8b. Przykład podziału ścieżki o skomplikowanym kształcie ze stykami złącza

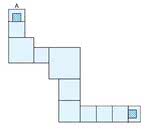
Powierzchnię ścieżki trzeba podzielić na kwadraty, na przykład w sposób przedstawiony na rysunku 8b. Rzeczywiste rozmiary kwadratów nie mają znaczenia, bo jak wykazano powyżej, ich rezystancje są jednakowe. Ścieżka składa się z sześciu kwadratów standardowych, trzech kwadratów narożnikowych i dwóch złączowych (jak na rys. 7). Zatem liczba kwadratów wynosi: 6 + 3 · 0,56 + 2 · 0,14 = 7,96, a rezystancja ścieżki od A do B - 7,96 · 0,48 mΩ = 3,82 mΩ. W taki sposób można obliczyć rezystancję ścieżek o nawet bardzo skomplikowanych kształtach. Proste mnożenie umożliwia potem obliczenie spadku napięcia i wydzielanej mocy w ścieżce.

A co z przelotkami?

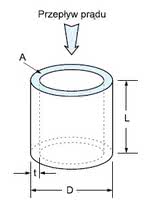
Często ścieżki usytuowane w różnych warstwach płytki są łączone przelotkami, których rezystancja też powinna zostać uwzględniona. Do ich obliczania posłużono się przedstawieniem o uproszczonej geometrii, pokazanym na rysunku 9. Przepływ prądu wzdłuż ścianek przelotki o przekroju "A", średnicy "D" i długości "L" wskazuje strzałka. Grubość miedzianych ścianek przelotki jest oznaczona "g". Rezystancję przelotki wyznacza zależność:

gdzie ρ oznacza rezystywność przewodnika, w tym przypadku 6 μΩ·cm przy 25°C. Warto zapamiętać, że miedź w przelotce ma rezystywność znacznie wyższą niż miedź czysta. Za grubość ścianki przelotki, niezależnie od grubości folii na płytce, można przyjąć g = 25 μm (1 mil).

Rys. 9. Geometryczne przedstawienie kształtu przelotki

Tabela 3. Rezystancje standardowych przelotek

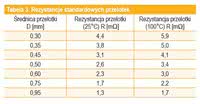
Dla płytki 10-warstwowej, złożonej z warstw 90 μm i folii 18 μm, L wynosi około 1,6 mm. W tabeli 3 zestawiono rezystancje przelotek o typowych wymiarach. (KKP)