Oscyloskop - gdy coś idzie nie tak
| TechnikaOscyloskopy cyfrowe mają wiele zalet, których nie miały oscyloskopy analogowe. Ale jak mówią Brytyjczycy "nie ma darmowych obiadów", co my Polacy, z naszym pesymistycznym nastawieniem do życia, rozszerzamy na "nie ma nic za darmo". Oscyloskopy cyfrowe z zasady swojego działania, zanim wyświetlą przebieg na ekranie, wykonują szereg operacji: próbkują badany sygnał, digitalizują go, zapisują dane w rekordzie akwizycji. Dzięki temu możliwe jest prowadzenie wszechstronnych pomiarów, analiza sygnału oraz jego archiwizacja. Próbkowanie niesie za sobą jednak wiele, często ukrytych komplikacji.
Aliasing, próbkowanie synchroniczne, interpolacja - to potencjalne przyczyny błędów interpretacji pomiarów oscyloskopowych. Aby ich uniknąć, trzeba te zagadnienia dobrze zrozumieć. Niestety większość producentów oscyloskopów cyfrowych nie poświęca tym kwestiom wiele miejsca, często trzeba je poznawać samemu poprzez własne eksperymenty i literaturę fachową.
Jest to więc dobry moment do omówienia tematu, a kto ma możliwość, również do przeprowadzenia własnych eksperymentów. Może w przyszłości uda się unikać pomyłek w pracy.
Aliasing
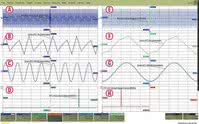
Rys. 1. Przykłady oscylogramów przebiegu sinusoidalnego o częstotliwości 400 kHz próbkowanego z różnymi szybkościami: a) próbkowanie 1 GSa/s, b) powiększony fragment przebiegu utworzony bez interpolacji, c) końcowa postać zrekonstruowanego przebiegu poddanego interpolacji sin(x)/x i powiększeniu, d) widmo sygnału A, e) przebieg próbkowany z szybkością 500 MSa/s, f) powiększony fragment przebiegu E utworzony bez interpolacji, g) końcowa postać zrekonstruowanego przebiegu E poddanego interpolacji sin(x)/x i powiększeniu, d) widmo sygnału E
Twierdzenie o próbkowaniu obowiązujące we wszystkich urządzeniach, w których zachodzi przetwarzanie analogowo- cyfrowe, mówi, że częstotliwość próbkowania musi być co najmniej dwa razy wyższa od najwyższej częstotliwości w sygnale. Jeżeli w oscyloskopie cyfrowym próbkowanie danego sygnału przebiega prawidłowo, to jest on rekonstruowany (wyświetlany na ekranie) na podstawie próbek bez utraty informacji.
W wyniku próbkowania sygnału niezgodnie z twierdzeniem o próbkowaniu, a więc z częstotliwością mniejszą niż podwójna maksymalna częstotliwość występująca w widmie sygnału, wystąpi zjawisko aliasingu. Każda składowa o częstotliwości niespełniającej twierdzenia o próbkowaniu da w wyniku przetwarzania analogowo-cyfrowego m.in. niskoczęstotliwościowe odbicie mieszczące się w zakresie częstotliwości roboczych.
Produkty takie nazywane są składowymi aliasingowymi. Częstotliwość wyznaczająca granicę, równa połowie częstotliwości próbkowania, jest nazywana częstotliwością Nyquista. Jest to więc najwyższa częstotliwość, która może być poddana próbkowaniu przy ustalonej częstotliwości próbkowania. Przykład aliasingu przedstawiono na rysunku 1.
Na oscylogramie A widoczny jest przebieg sinusoidalny o częstotliwości 400 MHz próbkowany z szybkością 1 GSa/s. Oznacza to, że liczba próbek przypadająca na jeden okres przebiegu jest równa 2½, co dobrze uwidoczniono na oscylogramie B. Oscylogram ten stanowi powiększony fragment całego przebiegu utworzony z surowych danych (bez interpolacji) znajdujących się w rekordzie akwizycji.
Jak widać, kształt tego przebiegu dość znacznie różni się od oryginału, ale nie wynika to z błędu próbkowania. Aby upodobnić wyświetlany przebieg do oryginału, w oscyloskopach cyfrowych stosowana jest interpolacja - najczęściej typu sin(x)/x. Efekt działania tej operacji jest widoczny na oscylogramie C. Z kolei na części D przedstawiono widmo sygnału oryginalnego (A) z wyraźnie widocznym prążkiem widma o częstotliwości 400 MHz.
Pomiar zmienia się radykalnie, gdy częstotliwość próbkowania spadnie poniżej częstotliwości Nyquista. Przypadek taki przedstawiono na oscylogramie E. Ten sam sygnał (400 MHz) jest teraz próbkowany z szybkością 500 MSa/s, w wyniku czego powstaje składowa aliasingowa o częstotliwości 100 MHz.
Powiększony fragment oscylogramu E utworzony bez interpolacji jest widoczny na rysunku F, a po zastosowaniu interpolacji na rysunku G. O błędzie pomiaru świadczy analiza FFT z wyraźnie widocznym prążkiem o częstotliwości 100 MHz (a nie 400 MHz). Warto zwrócić uwagę na to, że wykres widma kończy się na częstotliwości 250 MHz, czyli na częstotliwości Nyquista dla próbkowania 500 MSa/s.
O tym, że na ekranie może być wyświetlana składowa aliasingowa, nie rzeczywista, może świadczyć brak synchronizacji oscylogramu, który oczywiście trudno pokazać na papierze. W opisywanym pomiarze warunkiem wyzwalania było przejście narastającego zbocza sygnału przez poziom zerowy. W przebiegu próbkowanym prawidłowo wszystkie punkty spełniające warunek wyzwalania znajdują się w rekordzie wyzwalania, przebieg jest więc wyświetlany stabilnie.
W przebiegu, który powstał w wyniku aliasingu, część tych punktów nie znalazła się w rekordzie, a te, które spełniają warunek wyzwalania, zmieniają położenie w rekordzie, co powoduje utratę synchronizacji, a więc pływanie przebiegu wzdłuż osi czasu.
Jedną z metod sprawdzania, czy wyświetlany na ekranie przebieg powstał w wyniku prawidłowego przetworzenia sygnału wejściowego, czy na skutek aliasingu, jest jego obserwacja w dziedzinie częstotliwości. Proces próbkowania można porównać do mieszania sygnałów. Produkt końcowy powstaje w wyniku mnożenia przebiegu próbkowanego z bardzo wąskimi impulsami zegarowymi.
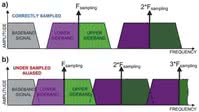
Rys. 2. Graficzna interpretacja procesu próbkowania w dziedzinie częstotliwości: a) prawidłowego, b) prowadzonego ze zbyt niską częstotliwością, w wyniku czego powstaje aliasing
Ale taki przebieg zegarowy jest z natury bardzo bogaty w harmoniczne. Zatem procesy takie jak próbkowanie i mieszanie wytwarzają szereg komponentów częstotliwościowych. Zawierają one wszystkie składniki częstotliwościowe sygnału próbkowanego, sygnału zegarowego i jego harmonicznych. W widmie sygnału wokół częstotliwości próbkowania i jej harmonicznych powstają odbicia widma sygnału próbkowanego (rys. 2).
Ogólnie przyjmuje się, że pasmo robocze rozciąga się do charakterystycznego kolana, powyżej którego częstotliwości są tłumione zwykle dość szybko, nie spadają jednak do zera gwałtownie. W rezultacie, próbkując sygnał zgodnie z kryterium Nyquista, a więc z częstotliwością dokładnie 2 razy większą od szerokości pasma roboczego, mógłby mimo to powstawać aliasing (wynikający z istnienia resztkowych częstotliwości za kolanem widma sygnału). Aby temu zapobiec, częstotliwość próbkowania jest odsuwana nieco dalej. Większość producentów stosuje próbkowanie z częstotliwością 2,5 razy większą od pasma.
Obniżanie częstotliwości próbkowania, wynikające na przykład z czynności pomiarowych, powoduje przesuwanie wszystkich produktów tego procesu w dół. Aliasing wystąpi, jeśli niższe składowe widma sygnału spróbkowanego pokryją się z pasmem sygnału oryginalnego. Jeśli w którymś momencie taki efekt się pojawi, poza ponownym zwiększeniem częstotliwości próbkowania lub wydłużeniem rekordu akwizycji nie będzie już żadnej metody na jego odwrócenie. Nie pomoże żadne filtrowanie. Pasmo robocze pozostanie zniekształcone.
Producenci oscyloskopów cyfrowych stosują kilka metod zapobiegania aliasingowi. Po pierwsze, należy wybierać częstotliwość próbkowania wielokrotnie wyższą od minimalnie wymaganej (oversampling). Często szybkość próbkowania jest 3 do 20 razy większa od częstotliwości Nyquista.
Po drugie, wydłużają rekord akwizycji, co pozwala utrzymać szybkość próbkowania nawet dla długich czasów akwizycji. Są to parametry, które warto przemyśleć przy zakupie oscyloskopu. Zalecane jest więc przeanalizowanie, czy dany model przyrządu zapewni rekord o wystarczającej długości dla wymaganych szybkości próbkowania potrzebnych do badania sygnału o określonym paśmie.

Rys. 3. Zależność szybkości próbkowania w funkcji podstawy czasu dla różnych długości rekordu akwizycji. Użyto oscyloskopu o paśmie 1 GHz i maksymalnej szybkości próbkowania 20 GSa/s. Należy zwrócić uwagę na to, że gdy szybkość próbkowania spadnie do 2 GSa- /s lub poniżej, wystąpi aliasing dla sygnału 1 GHz
Na rysunku 3 zilustrowano wpływ długości rekordu akwizycji na szybkość próbkowania oscyloskopu. Na wykresie podano szybkość próbkowania w funkcji podstawy czasu (czas/działkę) z długością rekordu jako parametrem. W przedstawionym eksperymencie oscyloskop miał pasmo 1 GHz i maksymalną szybkość próbkowania 20 GSa/s.
Dopóki szybkość próbkowania była większa od 2 GSa/s, dane były przetwarzane prawidłowo. Zmniejszenie tego parametru poniżej 2 GSa/s oznacza wejście w obszar, w którym może występować aliasing. Oscyloskop utrzymuje szybkość próbkowania 20 GSa/s dla tych nastaw podstawy czasu, które nie spowodują przepełnienia rekordu akwizycji.
Wydłużając podstawę czasu przy stałej szybkości próbkowania, musi jednak wystąpić moment, w którym dane nie zmieszczą się już w rekordzie. Oscyloskop automatycznie zmniejsza wówczas szybkość próbkowania. I tak, dla rekordu akwizycji o długości 10 k próbek szybkość próbkowania spadnie do 2 GSa/s, jeśli podstawa czasu będzie równa lub dłuższa od 500 ns/dz.
Wydłużając rekord do 100 k próbek, krytyczną szybkość próbkowania 2 GSa/s uzyskuje się dla podstawy czasu 50 μs/dz. Dalsze wydłużanie rekordu powoduje odsuwanie krytycznej szybkości próbkowania 2 GSa/s w stronę dłuższych podstaw czasu, zmniejszając tym samym możliwość występowania aliasingu.
Jako wskazówkę praktyczną można zaproponować, aby rozpoczynać pomiary od najszybszych podstaw czasu i stopniowo zmniejszać je w dół, w miarę potrzeb. Postępowanie takie pozwoli unikać aliasingu. Wydłużając podstawę czasu, od pewnego momentu szybkość próbkowania zaczyna maleć. Moment, w którym pojawia się aliasing, objawia się gwałtownym zmniejszeniem częstotliwości przebiegu wyświetlanego na ekranie i, jak wiemy, utratą synchronizacji. Jeśli taki efekt już wystąpi, jedynym ratunkiem jest wydłużenie rekordu akwizycji. Niektóre oscyloskopy dają użytkownikowi taką możliwość.
Próbkowanie synchroniczne
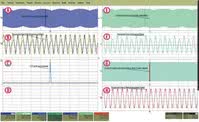
Rys. 4. Oscylogram utworzony w przypadku, gdy częstotliwość próbkowania jest wielokrotnością częstotliwości przebiegu mierzonego
Jeśli zegar taktujący próbkowaniem jest synchroniczny lub prawie synchroniczny z przebiegiem badanym, próbki są pobierane zawsze w tej samej fazie (lub w zbliżonej fazie). Oznacza to, że zawsze są próbkowane te same fragmenty przebiegu. Jest to najbardziej oczywiste szczególnie wtedy, gdy na jeden okres przypada tylko kilka próbek. Dopóki częstotliwość próbkowania spełnia kryterium Nyquista, nie ma w tym nic złego, ale oscylogram przybiera dość zaskakujący wygląd przypominający sygnał zmodulowany (rys. 4).
Próbkowany z częstotliwością 1 GSa/s sygnał przedstawiony na rysunku 4 miał pierwotnie częstotliwość 399,9 MHz. W trakcie eksperymentu zwiększano ją aż do wystąpienia efektu modulacji, co jest dobrze widoczne na oscylogramie A przedstawiającym pełną akwizycję. Częstotliwość "modulacji" jest równa 500 kHz (okres 2 μs).
W rzeczywistości jednak nie jest to efekt prawdziwej modulacji amplitudy. Widać to lepiej na powiększeniu (oscylogram B) utworzonym przy włączonej persystencji (sztucznej poświacie). Do tworzenia oscylogramu zastosowano interpolację liniową. Pojedynczy cykl akwizycji jest wyświetlony w kolorze niebieskim. Każdą próbkę uwidoczniono jako punkt na wykresie. Łatwo można obliczyć, że występują dwie i pół próbki na okres (pięć próbek na dwa okresy). Powiększony fragment z fragmentu B jest widoczny na oscylogramie A jako ciemniejszy pasek.
Funkcja persystencji dostępna w większości oscyloskopów cyfrowych pozwala śledzić historię wielu nakładających się na siebie akwizycji. Jak widać, po wielu cyklach akwizycji próbki tworzą regularny przebieg sinusoidalny. Położenie próbek bardzo nieznacznie zmienia się w kolejnych akwizycjach, więc choć na podstawie przebiegu wyświetlonego dla jednego cyklu akwizycji trudno zorientować się w kształcie sygnału oryginalnego, to historia zaznaczona persystencją daje już jego pełny obraz. Można zatem wnioskować, że przebieg jest tworzony prawidłowo, a efekt modulacji wynika tylko z ograniczonej liczby próbek przypadających na okres i dużej zgodności fazowej sygnału mierzonego z zegarem próbkowania.
Poprawność próbkowania potwierdza analiza FFT (część C). W widmie przebiegu jest widoczny tylko jeden prążek odpowiadający częstotliwości sygnału i nie obserwujemy charakterystycznych dla modulacji AM listków bocznych.
Oscylogram można poprawić, zwiększając liczbę próbek przypadających na okres przebiegu. Jedną z metod jest też zmiana interpolatora. Przebiegi wyświetlane na rysunkach A...C powstały w wyniku zastosowania interpolacji liniowej. W oscyloskopach cyfrowych domyślnie stosowana jest interpolacja sin(x)/x.
Ten algorytm interpolacji zastosowany do sygnałów o ograniczonym paśmie zapewnia najlepszą jakość rekonstrukcji sygnału próbkowanego. Najlepsze rezultaty uzyskuje się do częstotliwości 0,25...0,4 częstotliwości próbkowania. W opisywanym przykładzie częstotliwość sygnału jest równa 0,399 częstotliwości próbkowania (szybkość próbkowania równa 1 GSa/s).
Oscylogram E powstał właśnie z zastosowaniem interpolacji sin(x)/x. Jak widać, został on nieznacznie poprawiony, ale efektu modulacji nie wyeliminowano. Na powiększonym fragmencie F widzimy wprawdzie przebieg sinusoidalny, ale poszczególne jego okresy mają różne amplitudy. Nadal interpolator ma zbyt mało próbek przypadających na okres przebiegu.
W oscyloskopach wyższej klasy użytkownik może konfigurować funkcję interpolacji jako funkcję matematyczną. Jak skuteczna jest to metoda w konkretnych przypadkach, można wnioskować na podstawie oscylogramu G i H, który powstał w wyniku zastosowania własnej funkcji interpolacji przebiegu A. Obserwując powiększony fragment przebiegu na rysunku H, należy wnioskować, że problem został wyeliminowany całkowicie.
Inną metodą poprawiania jakości oscylogramu jest zwiększanie szybkości próbkowania i uzyskiwanie wystarczająco dużej liczby punktów do prawidłowego utworzenia oscylogramu. Jak już było wspomniane wcześniej, szybkość próbkowania można regulować, zmieniając podstawę czasu lub długość rekordu akwizycji.
Jeszcze raz należy podkreślić, że efekt "modulacji" nie jest błędem. Wszystkie funkcje pomiarowe oscyloskopu nadal dają prawidłowe wyniki, ponieważ są oparte na statystyce. Niemniej jednak wyświetlane na ekranie oscylogramy mogą wywoływać pewną konfuzję.
Uszy Gibbsa
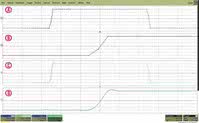
Rys. 5. Porównanie odpowiedzi interpolatora liniowego i sin(x)/x dla przebiegu prostokątnego o stromym zboczu
Interpolacja sin(x)/x działa bardzo dobrze z sygnałami sinusoidalnymi. Niestety, sygnały badane rutynowo mają często charakter cyfrowy i kształtem są zbliżone do przebiegu prostokątnego. Jeśli mają one strome zbocza, to w fazie przejściowej mieści się niewiele próbek, co stanowi problem dla interpolatora sin(x)/x.
Na rysunku 5 przedstawiono porównanie odpowiedzi interpolatora oscyloskopu na sygnał prostokątny o stromym zboczu. Przebieg z rysunku A powstał z zastosowaniem interpolacji liniowej. Rozciągnięte zbocze mierzonego przebiegu prostokątnego jest widoczne na rysunku B. Następny oscylogram - C, powstał w wyniku działania interpolatora sin(x)/x. Przebieg rozciągnięty w osi czasu jest widoczny na rysunku D.
Interpolator liniowy łączy próbki bezpośrednio odcinkami. W efekcie na oscylogramie nie powstają żadne przekroczenia na krawędziach przebiegu (pre-shoot i overshoot). Interpolator sin(x)/x ma w tych miejscach problem z dopasowaniem próbek do krawędzi. Wyraźnie jest obserwowane przekroczenie overshoot i mniej widoczne pre-shoot.
Artefakty te są nazywane czasami uszami Gibbsa. Użytkownicy oscyloskopów cyfrowych nie zawsze zdają sobie sprawę z tego, że nie są to rzeczywiste zniekształcenia przebiegu, a powstają one wyłącznie w wyniku pracy interpolatora. O faktycznym pochodzeniu takich zniekształceń można się przekonać, wybierając interpolację liniową i obserwując, czy przekroczenia zostały wyeliminowane.
Ogólnie interpolację liniową należy stosować dla przebiegów o charakterze impulsowym, natomiast sin(x)/x dla przebiegów sinusoidalnych. Trzeba też pamiętać, że efekt uszu Gibbsa będzie tym mniejszy, im więcej próbek przypadnie na krawędź zbocza impulsu.
Podsumowanie
Wykonując pomiary oscyloskopem cyfrowym, warto wyrobić w sobie kilka nawyków, które uchronią przed popełnianiem błędów omawianych w artykule, a więc:
- zapewniać możliwie najwyższą szybkość próbkowania.
- pomiary rozpoczynać od najszybszych podstaw czasu odpowiadających największym prędkościom próbkowania i stopniowo ją wydłużać, aż do ewentualnego wystąpienia aliasingu. Pojawienie się tego efektu oznacza, że nastawy oscyloskopu są złe.
- jeśli na ekranie nieoczekiwanie pojawia się oscylogram z przebiegiem modulowanym, włączyć funkcję Zoom i sprawdzić położenie próbek. Włączyć persystencję w celu obserwacji nakładających się na siebie przebiegów (tak jak na rys. 4). Jeżeli położenia próbek nie zmieniają się pomiędzy okresami przebiegu, można wnioskować, że wystąpiło próbkowanie synchroniczne, więc zegar próbkowania jest synchroniczny z przebiegiem badanym.
- jeśli w oscylogramach przebiegów impulsowych tworzonych interpolatorem sin(x)/x pojawiają się przekroczenia pre-shoot i overshoot, trzeba sprawdzić, czy nie znikają one po zastosowaniu interpolacji liniowej.
Podsumowując: korzyści wynikające z zastosowania w pomiarach oscyloskopu cyfrowego są znacznie większe niż ewentualne niedogodności, które są z tym związane. Nie należy więc zrażać się niepowodzeniami, ale zawsze trzeba wiedzieć, co poszło nie tak.
Jarosław Doliński