Powodem tego są niewątpliwe zalety architektury CT-ΣΔ, takie jak szybkość działania i łatwość implementacji. W artykule przybliżymy budowę, cechy i zasadę działania oraz porównamy przetworniki sigma-delta typu CT i DT.
Modulator delta
Modulacja delta została wynaleziona w latach 40. ubiegłego wieku. Inna nazwa tej techniki to różnicowa modulacja szerokości impulsu. Modulatory delta są również nazywane modulatorami z pojedynczym całkowaniem. W tej technice kwantowaniu podlega pochodna sygnału - różnica wartości sygnału pomiędzy kolejnymi próbkowaniami jest zamieniana na n-bitowe słowo cyfrowe. Jeśli zmiany sygnału pomiędzy kolejnymi próbkowaniami są małe, to długość słowa kodowego kwantyzera można zmniejszyć.
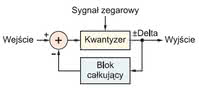
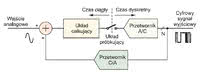
W granicznym przypadku, gdy częstotliwość próbkowania znacznie przewyższa częstotliwość sygnału, jego zmiany pomiędzy próbkowaniami są tak małe, że wystarcza kwantyzer 1-bitowy. Właśnie on jest głównym blokiem modulatora delta, pokazanego na rysunku 1a. W modulatorze delta sygnał wejściowy jest porównywany z sygnałem z bloku całkującego (integratora), a ich różnica jest podawana na kwantyzer.
Blok całkujący jest niczym innym, jak układem dostarczającym sygnał analogowy odpowiadający scałkowanej wartości impulsów z kwantyzera. Jeśli różnica pomiędzy sygnałami jest ujemna, kwantyzer generuje impulsy dodatnie, a ujemne, jeśli różnica jest dodatnia. W ten sposób uśredniona wartość sygnału z bloku całkującego podąża za zmianami sygnału wejściowego. Jeśli zmiany są zbyt szybkie (wartość delta lub częstotliwość próbkowania jest za mała), sygnał z bloku całkującego nie nadąża za sygnałem wejściowym i pojawia się błąd określany mianem slope overload.
Nietrudno o to zjawisko. Zakładając 16-bitowe przetwarzanie amplitudy, modulator delta potrzebuje 216 (65536) impulsów na okres częstotliwości próbkowania. Jeśli założymy sygnał audio, który należy próbkować z częstotliwością 44 kHz, to okaże się, że modulator delta musi być taktowany z częstotliwością bliską 3 GHz. Na szczęście wymyślono modulację sigma-delta.
Modulator sigma-delta
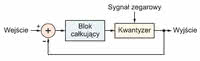
Modulacja sigma-delta, opracowana 20 lat po modulacji delta, eliminuje jej ograniczenia. W przetworniku sigma-delta kwantyzacji podlega różnica (delta) pomiędzy obecną wartością sygnału wejściowego i sumą poprzednich różnic. Blok całkujący znajduje się na wejściu kwantyzera, tak więc amplituda sygnału podawana na jego wejście nie zależy od częstotliwości sygnału. Z tego powodu modulatory sigma-delta są też nazywane modulatorami gęstości impulsów.
W modulacji sigma-delta kwantyzowany jest sygnał bezpośrednio, a nie jego pochodna, jak w modulacji delta. Z tego powodu maksymalny zakres napięcia wejściowego kwantyzera zależy od amplitudy sygnału wejściowego, a nie od składowych jego widma. Podobnie do modulacji delta, w celu uzyskania dużej rozdzielczości, wymaga się stosowania dużych częstotliwości próbkowania. Zaletą modulatorów sigma-delta jest natomiast kształtowanie widma szumu (noise shaping).
Modulator sigma-delta pierwszego rzędu pokazano na rysunku 1b. Na wejście kwantyzera podawana jest różnica między sygnałem wejściowym i skwantyzowaną wartością sygnału z bloku całkującego. W momencie, kiedy różnica pomiędzy sygnałem wejściowym i wyjściowym jest równa zeru, uśredniona wartość sygnału wyjściowego śledzi sygnał wejściowy. Blok całkujący jest w istocie filtrem dolnoprzepustowym dla sygnału różnicowego, przez co sprzężenie pętli ma również charakter dolnoprzepustowy.
Dzięki temu sprzężeniu zmniejsza się szum kwantyzacji dla małych częstotliwości, czyli szum na wyjściu przetwornika nie jest biały. W praktyce przetworniki pierwszego rzędu nie dają zadowalającej redukcji szumu, dlatego stosuje się systemy wyższych rzędów.
Przetwornik A/C sigma-delta
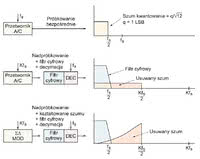
Rys. 3. Wpływ próbkowania nadmiarowego, filtracji cyfrowej, kształtowania charakterystyki szumowej oraz decymacji na jakość sygnału wyjściowego przetwornika
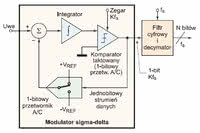
Uproszczony schemat blokowy przetwornika A/C sigma-delta (Σ-Δ) pokazano na rysunku 2. W schemacie blokowym można wyróżnić modulator sigma-delta i decymator. W celu uzyskania dużej rozdzielczości stosuje się nadpróbkowanie (oversampling) i kształtowanie szumu (noise shaping). Przyjrzyjmy się najpierw zaletom, jakie niesie ze sobą próbkowanie nadmiarowe. Rozważmy technikę nadpróbkowania w dziedzinie częstotliwości i zauważmy, że błąd kwantyzacji składowej stałej osiąga maksymalnie wartość ½ LSB (połowę wartości najmniejszego kwantu).
Wartość średniokwadratowa szumu kwantyzacji (rms) idealnego N-bitowego przetwornika A/C jest równa q/√12. Ta wartość jest równomiernie rozłożona w paśmie częstotliwości Nyquista od zera do fs/2, gdzie q jest wartością LSB, a fs częstotliwością próbkowania (rys. 3a). Z tego powodu stosunek sygnał/szum przy pełnym wysterowaniu sygnałem sinusoidalnym jest równy (6,02N + 1,76) dB. Jeśli przetwornik nie jest idealny i jego szum jest większy niż powyższe minimum szumu kwantyzacji, to efektywna rozdzielczość będzie mniejsza od N. Efektywną liczbę bitów (ENOB) definiuje się jako:
ENOB=(SN - 1,7dB)/6,02dB
Zwiększając częstotliwość próbkowania do Kfs, poszerzamy pasmo Nyquista, które w tym przypadku będzie obejmowało zakres od 0 do Kfs/2. Pasmo się rozszerza, ale wartość średniokwadratowa szumu pozostaje taka sama (q/√12), jak widać na rysunku 3b. Stosując dodatkowo cyfrowy filtr dolnoprzepustowy, usuwamy szum kwantyzacji, ale nie pogarszamy sygnału, a więc zwiększamy efektywną liczbę bitów przetwornika.
Dzięki tej technice można z dużą rozdzielczością przetworzyć sygnał analogowy przetwornikiem o małej liczbie bitów. Współczynnik K jest określany jako stosunek nadpróbkowania (Over Sampling Ratio - OSR). Ponieważ szum kwantyzacji jest rozpraszany na szersze pasmo, szum w wąskim paśmie (w którym znajduje się sygnał użyteczny) jest zmniejszony o współczynnik √K. Technika nadpróbkowania zmniejsza również wymagania na filtr antyaliasingowy, co jest bardzo ważne w tanich zastosowaniach konsumenckich.
Skoro szerokość pasma na wyjściu cyfrowego filtru dolnoprzepustowego jest mniejsza, to przy zachowaniu kryterium Nyquista wyjściowa częstotliwość może być mniejsza niż Kfs. W tym celu stosuje się decymator, który ze strumienia próbek Kfs wybiera co m-tą próbkę. Wartość m może być dowolna pod warunkiem, że częstotliwość strumienia próbek na wyjściu decymatora jest dwukrotnie większa niż pasmo sygnału użytecznego.
Decymator poprawia wydajność i dynamikę przetwornika A/C bez utraty informacji o sygnale użytecznym. Łatwo obliczyć, że uzyskanie rozdzielczości większej o n-bitów wymaga próbkowania z częstotliwością 22×n razy większą (1 bit więcej to nadpróbkowanie 4-krotne, 2 bity więcej to nadpróbkowanie 16-krotne itd.). Na szczęście w celu uzyskania dużej rozdzielczości nie trzeba w przetwornikach sigma-delta stosować dużych współczynników nadpróbkowania, gdyż oprócz ograniczania pasma sygnału uzyskujemy w nich wspomniane już kształtowanie szumu kwantyzacji.
Większość szumu znajduje się poza pasmem sygnału użytecznego, jak pokazano na rysunku 3c. Kształtowanie szumu polega na zmniejszaniu szumu kwantyzacji w paśmie użytecznym kosztem wzmacniania szumu poza tym zakresem. Po takim zabiegu szumy kwantyzacji są minimalne w paśmie użytecznym, a duże poza tym pasmem. Są jednak łatwe do wyeliminowania przez filtry dolnoprzepustowe. Prześledźmy zasadę działania przetwornika sigma-delta, zakładając sygnał stały na wejściu.
Sygnał na wyjściu bloku całkującego zmienia się w sposób ciągły od wartości minimalnej do maksymalnej i ma kształt przebiegu trójkątnego. Wyjście komparatora jest podane na wejście układu sumującego poprzez 1-bitowy przetwornik C/A. Uwzględniając znak sumowania, mamy do czynienia z ujemnym sprzężeniem zwrotnym w pętli. Powoduje ono, że średnia wartość napięcia na wyjściu przetwornika C/A jest równa wartości Uwe.
Z kolei średnia wartość napięcia na wyjściu przetwornika zależy od liczby jedynek i zer w strumieniu wyjściowym komparatora. Gdy wartość sygnału wejściowego Uwe rośnie, liczba jedynek w strumieniu wyjściowym komparatora również rośnie, a liczba zer maleje. W przeciwnym przypadku, gdy wartość sygnału wejściowego Uwe maleje, maleje również liczba jedynek w strumieniu wyjściowym komparatora, a liczba zer rośnie. Średnia wartość sygnału wejściowego Uwe jest kodowana w postaci szeregu impulsów komparatora.
Przetworniki sigma-delta z czasem dyskretnym i czasem ciągłym
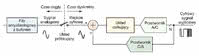
Pętlę sprzężenia zwrotnego modulatora i stosowany w niej filtr można zrealizować na dwa sposoby, jak pokazano na rysunku 4. W zależności od tego rozróżniamy przetworniki pracujące z czasem ciągłym (continuous time CT-ΣΔ) lub z czasem dyskretnym (discrete time DT-ΣΔ). Oba typy przetworników A/C składają się z tych samych elementów. Tyle że w przetwornikach z czasem dyskretnym stosuje się filtr z przełączanymi pojemnościami, a w przetwornikach z czasem ciągłym stosuje się filtry czasu ciągłego, np. gm-C, LC lub aktywne RC.
Na wejściach obu przetworników występują sygnały analogowe (ciągłe w czasie i amplitudzie), a na wyjściu sygnały cyfrowe (dyskretne w czasie i amplitudzie). W przetworniku pracującym z czasem dyskretnym modulator próbkuje sygnał wejściowy przed filtrem pętli, tak więc wymagany jest filtr antyaliasingowy. Dodatkowo, w celu eliminacji szpilek modulator czasu dyskretnego wymaga bufora odseparowującego sygnał ciągły z przełączanej pojemności wejściowego filtru dyskretnego.
Przykład przetwornika C/A sigma-delta CT drugiego rzędu pokazano na rysunku 5 wraz z charakterystyką szumu kwantyzacji (HN) i transmitancją układu (HS). Szum kwantyzacji jest funkcją dyskretną w dziedzinie czasu, dlatego określony jest wyłącznie w przedziale częstotliwości od 0 do fs/2. Z kolei transmitancja przetwornika jest określona dla wszystkich częstotliwości. Transmitancja układu dla częstotliwości powyżej fs/2 jest niezerowa, można więc spodziewać się zjawiska aliasingu.
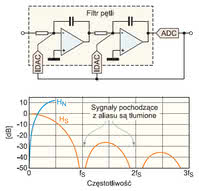
Rys. 5. Przetwornik sigma-delta czasu ciągłego drugiego rzędu oraz jego transmitancja dla sygnału Hs i szumu HN
Zwróćmy jednak uwagę, że w otoczeniu wielokrotności częstotliwości fs sygnał jest bardzo silnie tłumiony, czyli właśnie tam, gdzie sprawia największe problemy. Jak widać, nawet w systemie drugiego rzędu nie ma konieczności stosowania żadnych dodatkowych elementów. W systemach wyższego rzędu lub o większym współczynniku oversamplingu można spodziewać się jeszcze większego tłumienia aliasów. Generalnie, przetwornik A/C sigma-delta CT można uznać za kombinację filtru antyaliasingowego i przetwornika A/C.
Kolejna zaleta architektury CT jest związana z szumem. W systemie DT po filtrze dolnoprzepustowym w paśmie od 0 do fs/2 pojawiają się dodatkowe szumy związane ze zjawiskiem aliasingu. Z kolei w systemie CT aliasing występuje w tym miejscu pętli, które jest na niego mało wrażliwe. Tak więc przetworniki A/C sigma-delta CT potencjalnie charakteryzują się niższym poziomem szumu niż przetworniki sigma-delta DT. W przetwornikach z czasem dyskretnym to stopnie wejściowe (filtr) z przełączanymi pojemnościami ograniczają pasmo sygnału.
Czas przełączania i ustalania stopni wejściowych filtru jest wyznaczony poprzez wymaganą dokładność systemu. W trakcie akwizycji, czas ustalania zależy niestety również od stałej czasowej całego układu wejściowego i jego parametru slew rate. W przeciwieństwie do dyskretnych przetworników sigma-delta, przetworniki czasu ciągłego wymagają stosowania filtru całkującego wysokiego rzędu (opartego na wzmacniaczu operacyjnym), który jest łatwiejszy do sterowania ze względu na czysto rezystancyjny charakter impedancji wejściowej.
Ponieważ nie ma fazy akwizycji, nie ma też potrzeby stosowania układu próbkująco-pamiętającego. Nie wymaga się też, aby układy były szybkie. Przetworniki A/C sigma-delta czasu ciągłego nie są niestety pozbawione wad. Najistotniejsze z nich to ograniczony zakres częstotliwość próbkowania oraz wrażliwość na silne sygnały zaburzające spoza pasma użytecznego. Współczynniki filtru dolnoprzepustowego są uzależnione od częstotliwości próbkowania.
W przetworniku z czasem dyskretnym ustala się je, zmieniając stosunek pojemności filtru, a więc dość łatwo i precyzyjnie. Ustalenie dokładnych wartości współczynników jest łatwe również dlatego, że występujące rozrzuty produkcyjne ulegają w znacznym stopniu redukcji. Jeśli wartości nominalne rezystancji i pojemności wzrosną lub zmaleją, to ich stosunek się nie zmieni. Ponieważ szum cieplny kondensatora jest odwrotnie proporcjonalny do jego pojemności, uzyskanie najlepszego stosunku sygnału do szumu wymaga stosowania względnie dużych kondensatorów w filtrze.
W przetwornikach z czasem ciągłym współczynniki filtru wynikają ze stosunku stałej czasowej RC do okresu sygnału próbkującego. Niestety, stała RC podlega bardzo silnym fluktuacjom technologicznym. Dopasowanie współczynników filtru do częstotliwości próbkowania jest tutaj trudne, gdyż wymaga stosowania adaptacyjnych filtrów i kalibracji oraz banków przełączanych pojemności i rezystancji. Z tego powodów zakres częstotliwości próbkowania jest w przetwornikach z czasem ciągłym ograniczony.
W przetwornikach A/C sigma-delta najczęściej stosowane jest sprzężenie zwrotne (feedback) oraz sprzężenie wyprzedzające (feedforward). Sprzężenie wyprzedzające charakteryzuje się lepszym stosunkiem sygnału do szumu dla danego pasma i pobieranej mocy. Niestety, transmitancja przetworników A/C sigma-delta z czasem dyskretnym i sprzężeniem wyprzedzającym typowo nie ma charakterystyki filtru dolnoprzepustowego.
Ponadto, zwykle w zakresie większych częstotliwości poza pasmem użytecznym transmitancja osiąga duże wartości, a w szczególności mogą pojawić się w niej piki. Ponieważ te maksymalne wartości transmitancji znajdują się zazwyczaj jedną lub dwie oktawy powyżej pasma przepustowego, nie są problemem w aplikacjach, w których większa część energii sygnału jest skupiona w paśmie przepustowym lub w jego pobliżu. Inaczej jest jednak w aplikacjach komunikacyjnych, w których występują silne sygnały zakłócające o częstotliwościach dużo większych niż pasmo sygnału użytecznego.
W takich przypadkach konieczne jest zastosowanie dodatkowego filtru w celu tłumienia zakłóceń lub poświęcenie części zakresu dynamicznego przetwornika A/C. Przetworniki ze sprzężeniem zwrotnym mają dolnoprzepustową transmitancję, więc problem silnych zakłóceń poza pasmem użytkowym w nich nie występuje.
Inne usprawnienia architektury sigma-delta
Architekturę przetwornika sigma-delta można jeszcze usprawnić na kilka sposobów. Często stosowany jest wielobitowy kwantyzator zamiast jednobitowego oraz kaskadowe połączenia modulatorów. Stosując wielobitowe kwantyzatory zamiast jednobitowych, uzyskuje się szerszy zakres dynamiczny dla danego współczynnika nadpróbkowania i rzędu filtru pętli. Wadą tej techniki jest zależność liniowości od liniowości kwantyzera.
Do osiągnięcia 16-bitowej rozdzielczości konieczne jest trymowanie laserowe elementów kwantyzera. To sprawia, że wielobitowe architektury są mało praktyczne. Inna metodą jest stosowanie techniki MultistAge noise SHaping (MASH), która wykorzystuje kaskadowe połączenie przetworników pierwszego rzędu. W efekcie uzyskuje się przetwornik wyższego rzędu zbudowany z pojedynczych przetworników rzędu pierwszego, w których łatwo jest osiągnąć stabilność.
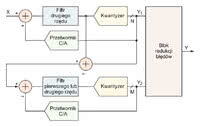
Wydajność układu MASH jest uzależniona od dopasowania pomiędzy jego analogowymi i cyfrowymi komponentami. Stosunek sygnał/szum na wyjściu przetwornika ulega szybkiej degradacji, jeśli szum kwantyzacji pierwszego kwantyzatora nie jest w pełni wyeliminowany w bloku redukcji błędów (rys. 6). Głównym źródłem problemów w tym układzie są wady komponentów analogowych, np. niewystarczające wzmocnienie wzmacniaczy operacyjnych czy rozrzuty produkcyjne parametrów.
Podsumowanie
Przetworniki A/C sigma-delta czasu ciągłego są atrakcyjnym rozwiązaniem, gdyż nie występuje w nich problem aliasingu, co eliminuje konieczność stosowania filtru. Co również istotne, nie wymagają one buforowania sygnału wejściowego, gdyż ich impedancja wejściowa ma charakter rezystancyjny. Przetworniki te cechują się dużym zakresem dynamicznym i doskonałymi parametrami szumowymi, co pozwala zmniejszyć wymagania na wzmocnienie i poziom szumów toru sygnałowego przed przetwornikiem.
Przetworniki sigma-delta czasu ciągłego z jedną pętlą sprzężenia i 1-bitowym modulatorem dobrze nadają się do aplikacji o paśmie użytecznym poniżej 5 MHz. Gdy wymagane jest szersze pasmo pracy, przetworniki z większą liczbą bitów kwantyzera wydają się bardziej adekwatne, choć trudno tu o generalne zasady. Z pewnością przetworniki sigma-delta czasu ciągłego ustępują przetwornikom z bezpośrednim przetwarzaniem pod względem szybkości (szerokości pasma użytecznego).
Dariusz Pieńkowski