Fraktale to obiekty matematyczne, które wyróżniają się właściwością samopodobieństwa w różnych skalach. Oznacza to, że przy przybliżaniu i oddalaniu każda ich część wygląda tak jak całość, tzn. wzory w ich strukturze powtarzają się przy różnych poziomach powiększenia. Fraktale przeważnie mają skomplikowane, pozornie nieregularne i abstrakcyjne kształty, których fantazyjność przyciąga uwagę. Wyróżniają je też wymiary będące zwykle liczbą niecałkowitą, określające, w jakim stopniu fraktale wypełniają przestrzeń, w której są osadzone.
Spopularyzował je matematyk Benoit B. Mandelbrot w latach 70. XX wieku, chociaż z elementami geometrii fraktalnej można było się spotkać już wcześniej w pracach innych naukowców. Mandelbrot zajął się badaniem możliwości opisywania w oparciu o nią natury, na przykład drzew, chmur czy linii brzegowych. On też wprowadził termin fraktal, który wywodzi się od łacińskiego przymiotnika fractus, który oznacza złamany albo pofragmentowany. W ten sposób nazwał kształty, których nie można opisać, opierając się na pojęciach geometrii euklidesowej, charakteryzujące się złożonością i pozorną chaotycznością, ale lokalnie uporządkowane dzięki powtarzalności wzorów je tworzących. Opracował też modele matematyczne i algorytmy do generowania i badania fraktali i stworzył zbiór Mandelbrota, będący prawdopodobnie najsłynniejszym fraktalem (rys. 1).

Praca Mandelbrota miała wpływ nie tylko na matematykę, ale znalazła też zastosowanie w różnych dziedzinach, jak fizyka, grafika komputerowa, biologia, ekonomia, architektura czy sztuka. Fraktale mają wiele zastosowań dzięki możliwości modelowania i reprezentowania za ich pośrednictwem skomplikowanych i samopodobnych struktur. Są wykorzystywane m.in. w: grafice komputerowej i animacji do generowania realistycznych krajobrazów, drzew, chmur, tekstur, technikach kompresji danych do zmniejszania rozmiaru plików, przetwarzaniu obrazów i sygnałów do wyodrębniania cech, rozpoznawania wzorców i rekonstrukcji, w biologii i medycynie na przykład do opisywania przebiegu wzrostu roślin i sposobu organizacji neuronów w mózgu. Znalazły także zastosowanie w projektowaniu kompaktowych, a jednocześnie wielopasmowych anten.
Miniaturyzacja
Główną zaletą konstrukcji fraktalnych jest możliwość znaczącego zmniejszenia rozmiarów anteny. Tradycyjny dipol półfalowy przy częstotliwości 2,4 GHz powinien mieć długość około 6,25 cm. To wydaje się niewiele, ale nie wówczas, gdy trzeba go wbudować w kompaktowe urządzenie, jak na przykład smartfon, czujnik Internetu Rzeczy, znacznik RFID, a tym bardziej smartwatch, opaskę fitness albo inne urządzenie elektroniki noszonej. Możliwość oszczędniejszego zagospodarowania dostępnego miejsca jest również ważna m.in. w dronach i satelitach.
W antenach fraktalnych zmniejszenie rozmiarów uzyskuje się dzięki złożoności kształtów fraktali. Typowe dla nich wielokrotnie powielane odcinki, pętle, zygzaki, zawijasy, załomy i rozgałęzienia, które uzyskuje się w kolejnych iteracjach powtarzających kształt bazowy, pozwalają na upakowanie na mniejszej powierzchni sumarycznie dłuższej ścieżki prądowej. Dzięki temu można wykonać anteny fraktalne o rozmiarach nawet 50‒70% mniejszych od ich tradycyjnych odpowiedników dla określonej częstotliwości. W praktyce więc pracują one na częstotliwościach znacznie niższych, niż wynikałoby to z ilości miejsca, jakie ostatecznie zajmą w urządzeniu. To pozwala na miniaturyzację bez rezygnacji z łączności w niskich pasmach częstotliwości.
Jak właściwości fraktali przekładają się na możliwość wydłużenia ścieżki prądowej anteny bez konieczności zwiększania zajmowanej przez nią powierzchni, najlepiej wyjaśnić na przykładzie krzywej Kocha. Jest ona także nazywana płatkiem Kocha, ponieważ przypomina płatek śniegu (rys. 2).
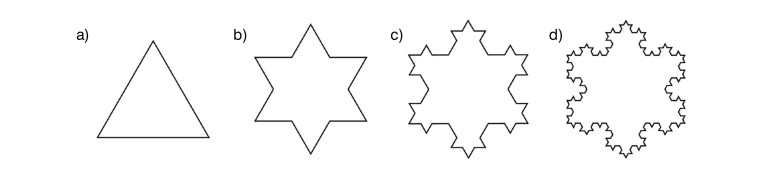
Płatek Kocha
Wzór podstawowy, który będzie wielokrotnie powielany, to w tym przypadku trójkąt równoboczny (rys. 2a). Przyjmijmy, że jego bok ma długość równą 1 cm. Stan początkowy (iteracja 0) jest zatem następujący: liczba boków 3, całkowity obwód 3 cm.
Procedura, którą trzeba powtórzyć w każdym kolejnym kroku, polega na tym, że każdy z 3 boków trójkąta jest dzielony na 3 równe części, każda o długości 1/3 cm. Następnie środkowa część boku jest usuwana i zastępowana dwoma bokami trójkąta równobocznego (rys. 2 b). Z każdego boku powstają zatem 4 segmenty, każdy o długości 1/3 cm. Po pierwszym kroku (iteracja 1) stan jest w związku z tym następujący: liczba segmentów 3 · 4 = 12, długość każdego segmentu: 1/3 cm, całkowity obwód: 12 · 1/3 = 4 cm. Oznacza to, że długość obwodu fraktala wzrosła o 33,33% (4/3 = 1,333).
W kolejnym kroku (iteracja 2) każdy z 12 segmentów o długości 1/3 cm jest dalej dzielony na 3 części, z których ta środkowa jest zastępowana dwoma bokami trójkąta (rys. 2 c). Zatem z każdego z 12 segmentów powstają 4 nowe. Stan jest wówczas następujący: liczba segmentów 12 · 4 = 48, długość każdego segmentu 1/3 ÷ 3 = 1/9 cm, całkowity obwód 48 · 1/9 = 48/9 = 16/3 = 5,333 cm. Obwód w tym kroku również zwiększa się o 33,33% (16/3 ÷ 4 = 4/3).
Po kolejnej powtórce (iteracja 3, rys. 2 d) stan to: liczba segmentów 48 · 4 = 192 segmenty, długość każdego segmentu: 1/9 ÷ 3 = 1/27 cm, całkowity obwód: 192 · (1/27) = 192/27 = 64/9 = 7,111 cm. Obwód również jest dłuższy o 33,33% (64/9 ÷ 16/3 = 4/3).
Jak wynika z tych obliczeń, przy każdej iteracji obwód fraktala Kocha wydłuża się o 4/3 (33,33%). Między drugą iteracją a stanem początkowym jego długość jest już o 77,78% większa. Natomiast po trzeciej iteracji obwód płatka jest o 137,04% dłuższy niż na początku. Co ciekawe, o ile obwód przy nieskończonej liczbie iteracji też dąży do nieskończoności, powierzchnia tego fraktala zmienia się w zupełnie inny sposób. Ta zależność jest wyróżnikiem płatka Kocha.
Aby obliczyć jego powierzchnię, w każdej iteracji trzeba zsumować pola rosnącej liczby trójkątów. Początkowo wynosi ona 0,43301 cm². Wartość tę podajemy z taką dokładnością celowo. Wynika to stąd, że z każdym kolejnym powieleniem wzoru początkowego wzrost powierzchni fraktala okazuje się coraz mniejszy. W pierwszych czterech iteracjach wynosi ona: 0,57735 cm², 0,64150 cm², 0,68259 cm² i 0,68263 cm². Oznacza to, że względem wartości startowej zwiększa się odpowiednio o: 33,33%, 48,13%, 57,63%, 57,64%. Oprócz tego przy nieskończonej liczbie iteracji, inaczej niż obwód, powierzchnia fraktala Kocha ma skończoną wartość 0,69282 cm².

Wielozakresowość
Kolejną zaletą anten fraktalnych jest łatwość uzyskania wielozakresowości i szerokopasmowości. Wynika to z najważniejszej cechy wyróżniającej fraktale, jaką jest samopodobieństwo. Dzięki niej składają się one ze wzorów, które replikują się w różnych skalach. W rezultacie w strukturze anteny fraktalnej obecne są elementy o różnej wielkości rozmieszczone w sposób regularny. Każda taka kopia kształtu bazowego w mniejszej skali ma inną częstotliwość rezonansową – dłuższe segmenty niższą, a krótsze – wyższą.
Im większa liczba iteracji, w wyniku których struktura fraktala się zagęszcza, tym szerszy zakres częstotliwości można objąć w ramach jednej konstrukcji. Stanowi to alternatywę tradycyjnego podejścia, w którym, aby pokryć kilka pasm częstotliwości, wykorzystuje się układy z osobnymi antenami i przełącznikami. Dzięki ich zastąpieniu jedną anteną, której poszczególne segmenty są dostrojone do różnych częstotliwości, można oszczędzić sporo miejsca i uprościć układ nadawczo-odbiorczy. Jest to korzystne zwłaszcza w urządzeniach przenośnych, które wymagają obsługi wielu pasm częstotliwości, a zarazem oszczędnego gospodarowania ograniczoną przestrzenią. Najlepiej wyjaśnić to na przykładzie projektu (uproszczonego) anteny zbudowanej z segmentów trójkąta Sierpińskiego, fraktala, który wyróżnia się na tle innych prostotą (rys. 3). Tworzy się go przez iteracyjne dzielenie trójkąta równobocznego na części i każdorazowe usuwanie środkowej z nich.
Trójkąt Sierpińskiego
Przyjmijmy, że długość boku trójkąta na początku (iteracja 0) wynosi 1 cm (rys. 3a). W pierwszym kroku (iteracja 1) łączymy środki jego boków, dzieląc go na cztery mniejsze trójkąty równoboczne. Każda z nowo utworzonych mniejszych figur ma długość boku równą połowie długości boku figury startowej. Następnie usuwamy trójkąt środkowy (rys. 3b). Stan po tej iteracji jest więc następujący: 3 trójkąty, każdy o boku długości 1 cm / 2 = 0,5 cm.
Dla wszystkich trzech trójkątów powtarzamy cały cykl: dzielimy każdy z nich na cztery mniejsze, a środkowy z nich usuwamy (rys. 3 c). Długość boku nowo powstałych trójkątów również będzie równa połowie długości boku ich "rodziców". Po iteracji 2 mamy zatem stan: 3 · 3 = 9 trójkątów, każdy o boku długości 0,5 cm / 2 = 0,25 cm. Można to też zapisać jako 1 cm / (2 · 2) = 1/4 cm. Po trzeciej iteracji z kolei stan zmieni się na następujący: 9 · 3 = 27 trójkątów, 0,25 cm / 2 = 0,125 cm, czyli 1 cm / (2 · 2 · 2) = 1/8 cm (rys. 3 d).

Załóżmy, że w oparciu o strukturę trójkąta Sierpińskiego chcemy zbudować antenę na zakres od 2,4 GHz (Bluetooth / Wi-Fi) do 5 GHz (Wi-Fi). Za startową długość boku trójkąta przyjmujemy połowę długości fali dla niższej częstotliwości, czyli 6,25 cm. W pierwszej iteracji otrzymamy trzy trójkąty o boku 6,25 / 2 = 3,13 cm. Ten segment anteny fraktalnej będzie miał więc częstotliwość rezonansową około 4,8 GHz. W zależności od materiału wykonania i dopasowania powinna ona móc obsłużyć również pasmo 5 GHz.
Projektowanie anten fraktalnych
Oprócz miniaturyzacji i umożliwienia pracy w wielu pasmach struktura fraktalna pozwala wpływać również na inne parametry anten. Na przykład umożliwia kształtowanie charakterystyki promieniowania. Dzięki złożonym kształtom fraktali prąd płynie bowiem ścieżkami o różnych długościach i orientacjach, w przeciwieństwie do anten tradycyjnych, w których rozkład prądu jest względnie przewidywalny, bo jest ograniczony ich prostą geometrią. Poszczególne segmenty ścieżki przewodzącej w strukturze fraktalnej można zatem traktować jako niezależne elementy promieniujące, z inną amplitudą i fazą prądu. Modyfikując ich parametry, można w związku z tym kontrolować lokalne nakładanie się pól elektromagnetycznych i uzyskać na przykład bardziej kierunkową charakterystykę promieniowania. Ponadto kształty fraktalne są łatwe do zoptymalizowania pod kątem konkretnych wymagań.
Po określeniu założeń projektowych takich jak częstotliwość, zysk, kierunkowość i współczynnik fali stojącej, należy wybrać rodzaj fraktala, na przykład krzywą Kocha lub trójkąt Sierpińskiego i określić wstępną liczbę iteracji. Zazwyczaj wystarczy jedna–dwie, a maksymalnie trzy. Im większa liczba iteracji, tym bardziej skomplikowany będzie kształt anteny. Równocześnie będzie można uzyskać na przykład większy stopień miniaturyzacji w porównaniu do anteny tradycyjnej dla takiej samej częstotliwości, obsłużyć większą liczbę pasm częstotliwości, uzyskać bardziej kierunkową charakterystykę promieniowania.
o przeprowadzeniu wstępnej symulacji projekt zazwyczaj wymaga dalszej optymalizacji. Podczas niej pod kątem parametrów docelowych modyfikuje się wymiary startowe (współczynnik skalowania), orientację i kąty rozgałęzień segmentów fraktala, testując różną liczbę iteracji dla całej struktury albo jej części, jeśli celem jest na przykład niesymetryczna charakterystyka promieniowania.
Postęp w dziedzinie produkcji struktur mikropaskowych umożliwia łatwe odwzorowanie kształtów fraktalnych na PCB. Ich złożoność geometryczna nie powoduje zatem zwykle znaczącego wzrostu kosztów produkcji anteny.
Monika Jaworowska














