Koprocesor arytmetyczny w STM32F4

Rys. 1. Liczba zmiennoprzecinkowa w postaci wykładniczej i jej przykładowa reprezentacja

Wsparcie w zakresie arytmetyki ograniczało się zwykle do możliwości mnożenia liczb stałoprzecinkowych w jednym cyklu zegarowym oraz do mnożenia i dodawania, a więc operacji ukierunkowanych pod kątem cyfrowego przetwarzania sygnałów (MAC).

Specjalizowany blok sprzętowy (FPU - floating point unit), przeznaczony do obliczeń na liczbach zmiennoprzecinkowych, pojawił się dopiero w najnowszych mikrokontrolerach z rdzeniem Cortex M4, w przypadku układów firmy ST Microelectronics są to mikrokontrolery z serii STM32F4.

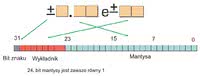
W świecie komputerowym liczby zmiennoprzecinkowe budowane są ze znaku, mantysy i wykładnika. Taka reprezentacja jest standardem opisanym przez normy, gdyż daje się w prosty sposób zakodować w kilku bajtach pamięci.

W większości języków programowania wysokiego poziomu liczby zmiennoprzecinkowe w takiej reprezentacji są obsługiwane jako tzw. float i mogą być o różnej precyzji, od half precision (16 bitów), przez single i double precision (32/64 bity) i quadruple precision (128 bitów).

Operacje zmiennoprzecinkowe są czasochłonne w realizacji za pomocą standardowych zasobów mikrokontrolera, gdyż za każdym razem wymagane jest dekodowanie operandów, modyfikowanie wartości, aby wykładniki były takie same, i ponowne kodowanie wyniku.

Stąd od wielu lat wydajne procesory wspomagane są układem sprzętowym realizującym operacje arytmetyczne na liczbach zmiennoprzecinkowych. Jednostka STM32F4 FPU to układ koprocesora o pojedynczej precyzji, komunikującego się z systemem mikroprocesorowym poprzez zawarty w układzie rejestr składający się z 32 rejestrów pojedynczej precyzji (S0-S31).

Za jego pomocą podawane są dane i odbierane wyniki obliczeń. Rejestr ten może być także adresowany jako 16 64-bitowych rejestrów podwójnej precyzji. Tryby działania i konfiguracja pracy układu FPU ustawiana jest w rejestrze FPSCR (Status and control register).

Definiuje on tryb zaokrąglania danych, zawiera flagi, takie jak znak minus, zero, przeniesienie i pożyczka. W rejestrze tym zawarte są również znaczniki błędów (wyjątków) w obliczeniach, np. dzielenia przez zero, ustawiony tryb zaokrąglania. Wyjątki takie są obsługiwane poprzez system przerwań.

FPU po resecie mikrokontrolera jest nieaktywny i jego aktywacja wymaga ustalenia poziomu dostępu kodu oprogramowania do koprocesora (zablokowany, pełny lub ograniczony) w rejestrze CPACR (Coprocessor Access Control).

Poza tym pracą FPU steruje 5 rejestrów systemowych, definiujących dane dotyczące m.in. stosu, funkcji FPU i danych kontekstowych. Układ FPU jest zgodny ze standardem IEEE.754, ale kilka operacji definiowanych przez tę normę zrealizowane zostało w sposób programowy:

• zaokrąglanie liczb zmiennoprzecinkowych do wartości zmiennoprzecinkowych zgodnych z formatem integer,
• konwersje danych z postaci binarnej do decymalnej i odwrotnie.

W stosunku do standardu IEEE.754 dodano też trzy niestandardowe tryby pracy:

• alternatywny format połówkowej precyzji AHP (alternative half precision), który ustawia tryb pracy 16-bitowej bez wykładnika i obsługi liczb nieznormalizowanych,
• Flush-to-zero FZ, w którym nieznormalizowane liczby (wykraczające przy obliczeniach poza format, czyli za małe lub za duże, wynik 0/0 lub nieskończoność) traktowane są jak zera,
• domyślny tryb NaN - FPU będzie tworzył NaN (not a number - nie liczbę), kiedy będziemy wykonywali np. dzielenie przez zero, pierwiastek z liczby ujemnej i nie spowoduje to wygenerowania błędu.

FPU dostarcza szybkich operacji zmien-noprzecinkowych poprzez rozszerzenie zbioru instrukcji. Dodatkowo FPU dodaje nowe rejestry danych, rejestr sterujący, rejestr stanu i kilka innych rejestrów wewnętrznych zorganizowane w stos.

Zestaw instrukcji FPU obejmuje rozkazy realizujące operacje arytmetyczne (dodawanie, odejmowanie, mnożenie, dzielenie, resztę z dzielenia i pierwiastkowanie), porównywanie, konwersję, zaokrąglanie oraz przechowywanie danych.

Większość z nich wykonywana jest w jednym cyklu zegara: ABS, negacja, dodawanie, odejmowanie oraz porównywanie danych i konwersja. Mnożenie, mnożenie z dodawaniem (MAC) i mnożenie z odejmowaniem zajmują 3 cykle zegarowe.

Natomiast dzielenie i pierwiastkowanie wykonują się w czasie trwania 14 cykli zegarowych. Uzupełniają je rozkazy przesuwania danych pomiędzy wewnętrznymi rejestrami FPU a pamięcią, ładowania i pobierania danych, które dostępne także dla bloków danych oraz odkładania i zdejmowania danych ze stosu.

W zestawie poleceń nie ma funkcji trygonometrycznych, wykładniczych i logarytmicznych, które są syntezowane z wymienionych komend elementarnych. FPU również wspiera różne całkowite i BCD typy danych, automatycznie konwertując je do i z tych typów danych, kiedy ładuje i przechowuje takie wartości.

Zarządzanie wyjątkami

Rys. 2. Struktura rejestru FPSCR

Koprocesor obsługuje pięć wyjątków podczas obliczeń, których zaistnienie powoduje wygenerowanie przerwania obsługiwanego przez sterownik przerwań. Są to:

• nieprawidłowe działanie, którego rezultatem jest NaN,
• dzielenie przez zero,
• wykonane Flush to zero,
• przepełnienie lub niedopełnienie, kiedy wynikiem jest liczba spoza formatu,
• niedokładny wynik spowodowany zaokrąglaniem, gdyż arytmetyka zmiennoprzecinkowa cierpi z powodu ograniczonej precyzji. W wyniku tego może wkraść się niedokładność do obliczeń. Kiedykolwiek dodajemy lub odejmujemy liczby, dokładność wyniku może być mniejsza niż precyzja dostarczona przez format zmiennoprzecinkowy.

Blokowanie i odblokowywanie przerwań i odczytywanie flag realizowane jest w kontrolerze. Wyjątkiem jest niedokładny wynik, który nie generuje przerwania i musi być obsługiwany programowo. Wygenerowanie przerwania jest tożsame z odłożeniem na stosie stanu FPU.

void GenerateJulia_fpu(uint16_t size_x, uint16_t size_y, uint16_t
offset_x, uint16_t offset_y, uint16_t zoom, uint8_t * buffer)
{
float tmp1, tmp2;
float num_real, num_img;
float radius;
uint8_t i;
uint16_t x,y;
for (y=0; y<size_y; y++)
{
for (x=0; x<size_x; x++)
{
num_real = y - offset_y;
num_real = num_real / zoom;
num_img = x - offset_x;
num_img = num_img / zoom;
i=0;
Radius = 0;
while ((i<ITERATION-1) && (radius < 4))
{
tmp1 = num_real * num_real;
tmp2 = num_img * num_img;
num_img = 2*num_real*num_img + IMG_CONSTANT;
num_real = tmp1 - tmp2 + REAL_CONSTANT;
radius = tmp1 + tmp2;
i++;
}
/* Store the value in the buffer */
buffer[x+y*size_x] = i;
}
}
}

Koprocesor we własnych programach

Przykładowy algorytm generacji fraktala Julii po uruchomieniu jednostki FPU i bez żadnych dodatkowych optymalizacji kodu, tylko poprzez dopisanie odpowiedniej deklaracji w opcji kompilatora, wykonał się od 11,5 do 17 razy szybciej.

Do testu wykorzystano płytę ewaluacyjną STM3240G-Eval oraz przykładowy kod GenerateJulia.c. Dla szybkiej arytmetyki zmiennoprzecinkowej oprogramowanie nie ma szans przeciwko sprzętowi.

Uzyskany wynik należy zakwalifikować jako dość duży i wskazujący, że jednostka FPU w Cortex-M4 jest w stanie znacznie poprawić wydajność całkowitą mikrokontrolera w aplikacjach złożonych obliczeniowo, takich jak sterowanie silnikami, generowanie grafiki trójwymiarowej, systemy sterowania działające w czasie rzeczywistym i w podobnych aplikacjach, gdzie wykorzystywane są filtry cyfrowe i przetwarzanie sygnałów.

Dla programisty użycie koprocesora w typowym przypadku nie wymaga żadnych działań poza jego aktywacją podczas kompilacji. Póki nie jest konieczne wykorzystanie specjalnych trybów pracy FPU, nie ma też potrzeby rozbudowania kodu, co zachęca do prób.

Robert Magdziak