Filtrowanie sygnału z przetwornika C/A

Poniedziałek, 08 października 2007 | Technika

Bardzo często projektanci w urządzeniach wykorzystujących przetworniki analogowo-cyfrowe implementują w kontrolerach bądź procesorach sterujących algorytmy uśredniające sygnał wyjściowy z przetwornika. Dzięki temu sygnał poddany konwersji zostaje wygładzony (rys. 1), a efektywna rozdzielczość przetwornika polepsza się.

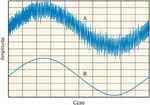
Rys.1. Zaszumiony sygnał (a) może być z powodzeniem wygładzony (b) przy użyciu filtru dolnoprzepustowego średniej kroczącej.

Wygładzanie sygnału z przetwornika dokonywane jest w następujący sposób. W pierwszej fazie próbki sygnału z przetwornika zbierane są z częstotliwością próbkowania, następnie dokonywane jest uśrednianie w obrębie grupy lub ustalonej liczby próbek, a cały proces jest powtarzany na wielu grupach w całym czasie obserwacji (rys. 2). Suma uśrednień daje w efekcie wygładzenie sygnału.

W kategoriach filtrowania, uśrednianie to jest niczym innym jak tylko filtrowaniem sygnału filtrem dolnoprzepustowym. Efektywność filtracji sterowana jest liczbą próbek w uśrednianej grupie. Większa liczba próbek w grupach polepsza efekt wygładzania. Ten proces filtracji eliminuje szpilki w przetworzonych danych, a także ogranicza pasmo sygnału.

Innym skutkiem ubocznym tej filtracji jest zwiększenie precyzji przefiltrowanych danych. W idealnym przypadku, średnia czterech próbek sygnału stałego zwiększa efektywną rozdzielczość przetwornika o jeden bit. A to z kolei, zgodnie ze znanym twierdzeniem poprawi stosunek sygnał szum na wyjściu przetwornika o 6 dB. Uśrednianie 16 próbek zwiększy rozdzielczość o 2 bity, a stosunek sygnał szum o 12 dB. Teoretycznie, liczba próbek w grupie równa 4N zwiększy efektywną liczbę bitów o N. Są jednak granice zwiększania liczby próbek w grupie.

Granice uśredniania

Zwiększanie efektywnej liczby bitów przetwornika analogowo cyfrowego możliwe jest dopóty, dopóki: liczba ta jest realna i nieidealności przetwornika brane są pod uwagę. Przykładowo, polepszenie rozdzielczości 12-bitowego przetwornika do 16 bitów wymaga zgodnie z wcześniejszymi rozważaniami uśredniania 256 próbek w każdym bloku. Rodzi się, więc pytanie czy jest wystarczająco dużo czasu na zaimplementowanie tego algorytmu w procesorze lub kontrolerze? Jeśli docelowa rozdzielczość jest większa niż 16 bitów, liczba próbek rośnie bardzo szybko. Nawiasem mówiąc 12-bitowy przetwornik powinien wykazywać się szumem o rozkładzie normalnym.

Czynniki nieidealne, które wpływają na liczbę próbek w grupie to przede wszystkim dryft wejść w czasie, zmiany napięcia zasilania, niestabilności napięcia referencyjnego oraz efekty termiczne. Każde z wymienionych zjawisk może wpłynąć na błąd przetwarzania. Liczba próbek w systemie nieidealnym może się zmniejszyć z 2000 do kilkuset, gdyż zwiększanie liczby próbek w systemie nieidealnym „zaszumia” wynik i efekt jest odwrotny do zamierzonego. Można jednak stosując metodę wariancji Allana wyliczyć optymalną liczbę próbek do uśredniania tak, aby wypośrodkować między filtracją a zaszumieniem. W końcu ważny jest moment ustalenia sygnału wejściowego przetwornika oraz jego czystość widmowa. Składowe harmoniczne pochodzące np. z zasilania siecią 50 Hz wpłyną na maksymalną liczbę próbek w grupie.

Rys. 2. Algorytm obliczania średniej kroczącej. Liczba próbek w grupie wynosi tu 4.

Nie zawsze można i należy filtrować z maksymalną liczbą próbek w grupie. Wszystko zależy od sygnału na wyjściu przetwornika. Inaczej, gdy jest to sygnał szybkozmienny, inaczej, gdy jest to sygnał stały. Częstotliwość graniczna filtru ze średnią kroczącą jest odwrotnie proporcjonalna do liczby próbek w grupie. Im większa liczba próbek przy stałej częstotliwości próbkowania tym niższa częstotliwość graniczna. Aby nie odfiltrować użytecznego sygnału, trzeba czasem arbitralnie ustalić liczbę próbek.

Trochę czasu można oszczędzić

Istnieją również oszczędniejsze w czasie algorytmy uśredniające, które wykraczają poza brutalną metodę zbierania danych, a później obliczania z nich średniej. Przykładowo kolejka FIFO (First In First Out) może być użyta do tego celu poprzez dodanie nowej danej i odejmowanie wartości pierwszej danej w grupie. Dodatkowo rozmiar grupy tak się wybiera by umożliwić operację dzielenia jako przesuwania w prawo, a więc liczba wartości w grupie wynosi 8, 16, 32 lub więcej. Niezależnie od wybranej metody, filtry ze średnią kroczącą wygładzają przebieg wyjściowy przetwornika i poprawiają rozdzielczość poprzez redukcję szumu.

Dariusz Pieńkowski