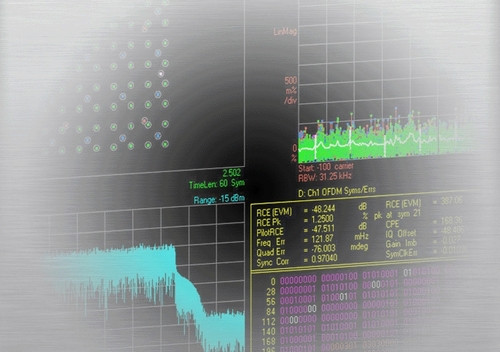
Dyskretna transformata Fouriera

Rys. 1. Typowy system DSP.

Dyskretna transformata Fouriera (DTF) jest szeroko stosowana w aplikacjach przetwarzania sygnałów, jak na przykład w telekomunikacji. Równania DTF często zniechęcają projektantów również w innych dziedzinach do zapoznawania się z literaturą przetwarzania sygnałów cyfrowych. Wraz z rozwojem technologii przetwarzania analogowo-cyfrowego (ADC) i cyfrowo-analogowego (DAC) obszar DSP obejmuje coraz więcej układów analogowych. Na przykład we współczesnym odbiorniku software’owym sygnał w.cz. opuszcza domenę analogową już we wstępnej części odbiornika i jest przetwarzany w cyfrowy w stopniu częstotliwości pośredniej. Typowy system DSP jest przedstawiony na rys. 1.

Rys. 2. Odnajdywanie podobieństw przebiegów.

Sygnał analogowy jest próbkowany i kwantowany w przetworniku A/C i w postaci szeregu cyfr doprowadzany do DSP. Programowalny DSP o odpowiedniej architekturze, przygotowanej do równoczesnego operowania danymi i instrukcjami, wykonując zadania przetwarzania sygnału. W przetworniku C/A sygnał jest z powrotem przetwarzany w analogowy. Dla projektantów układów w.cz. i analogowych zrozumienie DTF jest zatem niezbędne.

Transformata Fouriera dla umożliwienia analizy częstotliwościowej przekształca sygnał z domeny czasu w domenę częstotliwości. Jednakże transformata Fouriera jest ciągłą funkcją częstotliwości i nie nadaje się do obliczeń w DSP. Analizę komputerową umożliwia przedstawienie przez DTF sygnału ciągłego w czasie. Wyprowadzenie DTF trzeba zacząć od pojęcia prostej korelacji.

Korelacja punktowa

Rys. 3a. Sygnał ciągły w czasie.

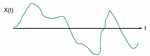
Na pytanie, który z przebiegów 2 i 3 na rys. 2 jest bardziej podobny do przebiegu 1 można próbować odpowiadać intuicyjnie, ale odpowiedź nie zawsze będzie poprawna. Istnieje jednak metoda mierzenia podobieństwa dwóch funkcji lub przebiegów. W przetwarzaniu sygnałów nazywa się ona korelacją.

Korelacji używa się do oceny odebranego sygnału o znanych cechach. Można na przykład odzyskać falę nośną z zakłóconego odebranego sygnału przez skorelowanie go z generowanym lokalnie „czystym” sygnałem zegarowym. Różnica pomiędzy sygnałem odebranym a dopasowywanym i błąd dopasowania służą do korygowania fazy i częstotliwości oscylatora. Przy modulacji z widmem rozproszonym koreluje się wzór generowanych lokalnie pseudo-zakłóceń z wzorem odebranych i koryguje fazę oscylatora przed demodulacją danych.

W literaturze DSP korelację matematycznie opisuje się równaniem

Rys. 3b. Sygnał próbkujący.

Równanie to przedstawia korelację y(τ) dwóch funkcji x1(t) i x2(t) jako funkcję przesunięcia w czasie τ. Dla każdej wartości tego przesunięcia obie funkcje są mnożone, a rezultat całkowany w całym obszarze nieskończoności. Dla funkcji okresowych równanie to przybiera postać

Jak widać, całkowanie i uśrednianie jest dokonywane w pojedynczym okresie T, sygnały bowiem są teraz sygnałami potęgowymi. Następnie można wprowadzić uproszczoną wersję powyższego równania, bez przesunięcia w czasie. Korelację y nazywa się teraz korelacja punktową.

Rys. 3c. Sygnał nieciągły w czasie.

Równanie korelacji punktowej, będące po prostu średnią iloczynu dwóch sygnałów okresowych za okres, jest miarą podobieństwa x1(t) i x2(t) bez przesunięcia czasowego τ pomiędzy nimi, czyli korelacją w punkcie. Zatem korelacja punktowa ustala stopień dopasowania tych dwóch funkcji. Taka interpretacja jest pomocna do zrozumienia równań DTF. O ile korelację można rozpatrywać jako poszukiwanie jednej funkcji w drugiej, to korelację punktową można uważać za miarę stopnia wbudowania jednej funkcji w drugą. Jest średnią sumy iloczynów tych dwóch funkcji lub sygnałów, za okres będący przedmiotem zainteresowania.

Nieciągła korelacja punktowa

Rys. 4. Okresowy ciąg impulsów (a) i odpowiadający mu szereg Fouriera (b).

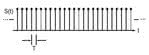
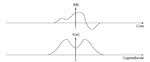
Rezultatem próbkowania ciągłego sygnału x(t), pokazanego na rys. 3a, za pomocą pokazanego na rys. 3b sygnału próbkującego o stałym okresie T, jest sygnał nieciągły w czasie o niezerowych wartościach w momentach nT, pokazany na rys. 3c. Można napisać równanie korelacji punktowej dwóch sygnałów nieciągłych w czasie o N próbkach

Z porównania tego równania z równaniem korelacji dla funkcji okresowych 1 widać, że całkowanie za okres T sygnałów ciągłych w czasie zostało zastąpione przez sumowanie N składników sygnałów nieciągłych w czasie. Opuszczając dla uproszczenia w powyższym równaniu odstęp pobierania próbki T otrzymuje się

Składniki x1(n) i x2(n) przedstawiają teraz sekwencje N liczb, a y jest sumą ich iloczynów w przedziale T. Równanie powyższe tym samym przedstawia nieciągłą korelację punktową.

Szereg Fouriera

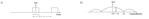
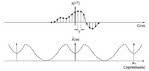
Rys. 5. Gdy okres zmierza do nieskończoności (a), sygnał okresowy staje się nieokresowym (b), a odstępy częstotliwości w szeregu Fouriera zbliżają się do zera. Powstaje transformata Fouriera.

Rozwinięcie w szereg jest próbą przedstawienia dowolnego sygnału za pomocą zbioru sygnałów (zwanych funkcjami podstawowymi) o znanych parametrach, jak amplituda, częstotliwość i faza. Suma wszystkich składników zbioru jest przybliżeniem tego sygnału. Różnicą pomiędzy oryginałem i odwzorowaniem jest błąd, wyrażany w postaci odchylenia średniokwadratowego.

Według Fouriera dowolny sygnał okresowy x(t) daje się przedstawić jako sumę nieskończonej liczby sinusoid o częstotliwościach harmonicznych z częstotliwością podstawową ω0 z odpowiednimi amplitudami i fazami. Innymi słowy, każdy sygnał okresowy można rozłożyć na nieskończoną liczbę sinusoid o częstotliwościach będących całkowitymi wielokrotnościami podstawowej częstotliwości ω0 tego sygnału. Funkcję x(t) można rozwinąć w szereg Fouriera w sposób następujący

Rys. 6a. Nieokresowy sygnał ciągły w czasie i jego nieokresowe ciągłe widmo częstotliwości.

W skład x(t) wchodzą wszystkie składowe sinusoidalne i cosinusoidalne. Stała a0 odpowiada składowej stałej, czyli wartości napięcia (prądu) stałego (o częstotliwości zerowej) x(t) . Współczynniki an i bn wyznaczają amplitudy składowych sinusoidalnych i cosinusoidalnych, czyli wielkości ich wkładów w x(t). Jak można znaleźć wartości an i bn? Ponieważ an jest amplitudą n-tej harmonicznej sygnału cosinuidalnego zawartego w sygnale x(t), to okazuje się, że jest korelacją punktową cosinusa i x(t). Współczynniki an i bn otrzymuje się z równania na korelację punktową 2.

oraz

Równanie 3 można napisać w postaci wykładniczej

oraz

Rys. 6b. Nieokresowy sygnał nieciągły w czasie ze swoim okresowym ciągłym widmem częstotliwości.

Ciągły sygnał okresowy może zostać rozłożony na nieskończony zbiór, zwany szeregiem Fouriera, harmonicznie zależnych częstotliwości, dla których częstotliwością podstawową jest odwrotność okresu.

Transformata szeregu Fouriera

Rys. 6c. Okresowy sygnał nieciągły w czasie i jego okresowe nieciągłe widmo częstotliwości.

Szereg Fouriera w domenie częstotliwości przedstawia jedynie sygnały okresowe w czasie. Niestety jednak nie wszystkie sygnały są okresowe. Przykładami sygnałów nieokresowych w czasie są mowa, muzyka, czy wideo. Konieczna więc jest jakaś metoda przedstawiania takich sygnałów w domenie częstotliwości. Umożliwia to właśnie transformacja Fouriera. Równania transformacji Fouriera można otrzymać z równań szeregu Fouriera kilkoma prostymi krokami zilustrowanymi na rys. 4.

Z ciągu impulsów prostokątnych o okresie T i długości t, widocznego na rys. 4a, otrzymuje się częstotliwościowe przedstawienie tego sygnału za pośrednictwem równania 4 szeregu Fouriera. Szereg ten jest uwidoczniony na rys. 4b prążkami częstotliwości, rozmieszczonymi co 1/T Hz, a jego obwiednia odzwierciedla funkcję sin(x)/x z zerem przy 1/t Hz. Przykład ten pomaga intuicyjne przedstawić sobie transformację szeregu Fouriera, gdy sygnał nie jest okresowy. Zwiększenie okresu T w domenie czasu powoduje zmniejszenie odstępów prążków częstotliwości szeregu Fouriera w domenie częstotliwości, ponieważ odstępy te są równe częstotliwości podstawowej f0 = 1/T. Jeżeli T rośnie do nieskończoności, sygnał okresowy staje się nieokresowy, jak to widać na rys. 5a, a odstępy linii w widmie dążą do zera, co jest pokazane na rys. 5b, czyniąc to widmo ciągłym. To właśnie jest transformacja Fouriera.

Szereg Fouriera w równaniu 3 musi zatem zostać zmodyfikowany przez zastąpienie sumacji całkowaniem, a nieciągła częstotliwość nω0 ciągłą częstotliwością ω. Równanie 3 redukuje się do transformaty Fouriera, przedstawionej poniżej

która może być napisana w postaci wykładniczej

Rys. 7. Nieokresowy sygnał nieciągły w czasie (a) zostaje zokienkowany (b), a jego zokienkowany segment jest odtwarzany (c) tworząc sygnał okresowy, dla którego można obliczyć DTF.

Współczynnik, czyli moduł, X(ω) składnika wykładniczego ejw poprzez wykładnik zmniejsza błąd pomiędzy rzeczywistym sygnałem a jego przybliżeniem i zostaje otrzymany za pomocą korelacji punktowej

A zatem X(ω) przedstawia, ile z ejωt znajduje się w x(t). Równania 5 i 6 tworzą parę transformat Fouriera.

Nieciągła transformacja Fouriera

Trzeba przyjrzeć się dokładnie równaniom 5 i 6. Do znalezienia x(t) i X(ω) trzeba scałkować iloczyn dwóch ciągłych funkcji w przedziale nieskończoności. Matematycznie wszystko jest w porządku, ale gdy trzeba znaleźć transformatę Fouriera w zastosowaniu praktycznym, w czasie rzeczywistym, nie jest to możliwe. Do znalezienia użytecznego rozwiązania konieczne są jakieś sztuczki. Po pierwsze w praktyce ma się do czynienia z sygnałami o skończonym czasie trwania i z widmami o skończonej szerokości pasma. Po drugie, próbki sygnału muszą mieć określoną długość, a widmo określone częstotliwości składowe. Osiąga się to w następujący sposób.

Przykładowy ciągły w czasie nieokresowy x(t) jest pokazany na rys. 6a. Jego fourierowska transformata X(ω) jest ciągła i nieokresowa w domenie częstotliwości. Sygnał próbkuje się w odstępach T, czyniąc go nieciągłym w czasie. Zgodnie z jednym z twierdzeń w przetwarzaniu sygnałów mnożenie w domenie czasu odpowiada splotowi w domenie częstotliwości i na odwrót. Ponieważ próbkowanie jest mnożeniem x(t) i sygnału próbkującego s(t) w domenie czasu, odpowiada ono splotowi widma sygnału z widmem s(t), będącego szeregiem harmonicznych fs, pokazanym na rys. 6b. Jeśli pamięta się proces i widmo modulacji amplitudy, można rozpoznać, że widmo z rys. 6b jest widmem modulacji każdej harmonicznej fs przez s(t). Splot jest właśnie tym procesem.

Następnym krokiem jest przemiana tego widma w nieokresowe przez próbkowanie z częstotliwością ω0 Hz. Zabieg ten w domenie częstotliwości wpływa na sygnał w domenie czasu czyniąc go okresowym, pokazanym na rys. 6c. Jest to wynik splotu sygnału z ciągiem impulsów próbkujących o okresie 1/f0. Powstał w ten sposób nieokresowy w czasie sygnał i jego okresowa transformata fourierowska. Rozciągają się one do nieskończoności, ale są okresowe. Trzeba więc wziąć jeden okres w każdej z domen mnożąc go przez funkcję prostokątną. Zabieg ten nazywa się okienkowaniem. Okienkowanie w jednej domenie wpływa oczywiście na sygnał w drugiej domenie. Jeden okres otrzymanego widma nieokresowego przyjmuje się więc za nieokresową fourierowska transformatę jednego okresu nieciągłego sygnału okresowego. Poniższe dwa równania są równaniami syntezy i analizy DTF.

Z równania syntezy wynika, że zbiór N próbek w czasie można rozłożyć na N funkcji wykładniczych (składników sinusowych i cosinusowych) o amplitudach określonych przez równanie analizy. A zatem każdy X(k) reprezentujący amplitudy składników sinusowych i cosinusowych można otrzymać z korelacji punktowej N próbek segmentu sygnału i N próbek składników sinusowych i cosinusowych. Obliczenie każdej wartości X(k) wymaga N mnożeń, a ponieważ istnieje N wartości k, do obliczenia DTF potrzeba N2 mnożeń.

W praktyce do analizy sygnałów przy pomocy DTF, najpierw trzeba przez próbkowanie otrzymać sygnał nieciągły, jak pokazano na rys. 7a i wydzielić segment N próbek przez okienkowanie, jak pokazano na rys. 7b. Następnie przyjmuje się, że segment jest powtarzalny, czyli segment zostaje powielony w obie strony, jak pokazuje rys. 7c. Dla tego sygnału używając równania 7 oblicza się współczynniki jednego okresu nieciągłej transformaty Fouriera. Następnie przenosi się na następny segment ciągu próbek i powtarza się obliczenia współczynników DTF. Przedstawienie poprzez próbki transformat Fouriera jest w gruncie rzeczy przedstawieniem poprzez ciąg okresowy ciągu o ograniczonej długości, którego jeden okres jest skończoną sekwencją, która ma zostać przedstawiona.

Fizyczne znaczenie transformaty, rozumianej poprzez korelację punktową, może pomóc w zrozumieniu DTF i usunąć powszechne wśród inżynierów zniechęcenie do równań transformaty wynikające z konieczności zastosowania złożonego aparatu matematycznego.

Krzysztof Pochwalski