FFT w oscyloskopach cyfrowych - poradnik użytkownika

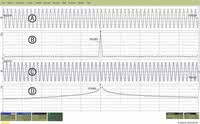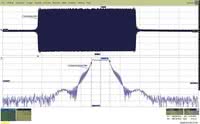
Rys. 1. Oscylogram przedstawiający impulsowo zmodulowany przebieg w.cz.: a) w dziedzinie czasu, b) w dziedzinie częstotliwości. Sygnał zajmuje pasmo od 997 MHz do 1002 MHz

Aparat matematyczny wykorzystywany do realizacji funkcji FFT jest na tyle złożony, że prawdopodobnie duża część użytkowników nawet nie próbuje go dokładnie poznać. Pomyśleć, że podwaliny tej teorii zawdzięczamy żyjącemu dwa wieki temu Jeanowi Baptiste Josephowi Fourierowi, który nawet nie mógł przypuszczać, że kiedykolwiek zostanie skonstruowany taki przyrząd jak oscyloskop.

Od razu uspokajamy zaniepokojonych czytelników. Nie, nie będziemy tu zamieszczać wykładu z matematyki, w każdym razie teoria zostanie ograniczona do minimum. Pokazane natomiast zostaną praktyczne wskazówki przydatne w pomiarach widma z użyciem funkcji FFT.

Pierwsze implementacje FFT pojawiły się równocześnie z rozpoczęciem komercyjnego stosowania mikroprocesorów w sprzęcie elektronicznym, są więc datowane mniej więcej na rok 1970. Obecnie z FFT korzystają zarówno użytkownicy najdroższych oscyloskopów, jak i amatorzy posiadający przyrządy najtańsze. Funkcja FFT jest bardzo przydatnym narzędziem wykorzystywanym do analizy widma sygnałów, jednak efektywne jej użycie wymaga znajomości pewnych zagadnień. W artykule wyjaśniono zasady optymalnego dobierania nastaw oscyloskopu pod kątem uzyskiwania najlepszych wyników pomiaru widma.

Dwie dziedziny

Na rysunku 1 przedstawiono sygnał sinusoidalny zmodulowany amplitudowo sygnałem trapezowym. W górnej części jest widoczny przebieg w dziedzinie czasu, w dolnej części oglądamy jego widmo. Patrząc wyłącznie na przebieg czasowy trudno nawet w przybliżeniu oszacować szerokość widma badanego sygnału. Niemal od razu można na to pytanie odpowiedzieć patrząc na oscylogram utworzony za pomocą funkcji FFT. W przedstawionym na rysunku 1 sygnale zastosowano liniowe przemiatanie częstotliwości. Za pomocą kursorów szybko określamy szerokość pasma, która w tym przypadku jest równa 4,7 MHz.

Częstotliwościowy zakres analizy FFT (span) i rozdzielczość pomiaru pasma (RBW)

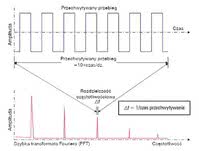
Rys. 2. Rozdzielczość widma (RBW) równa odwrotności długości rekordu określanej w dziedzinie czasu, (odwrotności czasu akwizycji)

Jak wiadomo, częstotliwość sygnału okresowego jest równa odwrotności jego okresu. Zależność ta obowiązuje w pełni również dla funkcji FFT i warto o niej pamiętać podczas konfigurowania oscyloskopu do pomiaru widma. Jednym z parametrów funkcji FFT jest rozdzielczość - RBW (Df, resolution bandwidth), określająca najmniejszy przyrost częstotliwości, jaki można zaznaczyć i zmierzyć na wykresie widma. Jest to więc różnica częstotliwości pomiędzy dwiema sąsiednimi "komórkami" widma. W dziedzinie czasu najmniejszy, dający się zmierzyć interwał jest natomiast określony przez okres próbkowania.

Dalsze rozważania prowadzą do prostego wniosku, że RBW jest odwrotnością długości rekordu akwizycji, ale określanej w jednostkach czasu. Czas wypełniania rekordu akwizycji próbkami jest nazywany czasem przechwytywania. Interpretację tych pojęć przedstawiono na rysunku 2.

W oscyloskopach nie ma jednak pokrętła służącego do bezpośredniego ustawiania RBW, można jedynie regulować podstawę czasu mierzoną w jednostkach czas/działkę, odpowiadającą skalowaniu osi poziomej wykresu czasowego. Przykładowo, jeśli czas akwizycji w pomiarze z rysunku 1 jest równy 20 ms, to rozdzielczość pomiaru widma RBW, jako odwrotność czasu akwizycji jest równa 50 kHz.

Następnym krokiem konfigurowania funkcji FFT jest określenie zakresu częstotliwości wyświetlanego widma, czyli częstotliwości minimalnej i maksymalnej. Najczęściej wybierany zakres rozpoczyna się od częstotliwości 0 Hz i rozciąga się aż do częstotliwości maksymalnej. W prawdziwych analizatora widma operacje te wyglądają inaczej, co będzie wyjaśnione w dalszej części artykułu.

Zakres analizy FFT (span) jest równy połowie efektywnej szybkości próbkowania (rys. 3). Najmniejszy przyrost czasu - okres próbkowania, determinuje największy element w dziedzinie częstotliwości. Podobnie jak najmniejszy element mierzony w dziedzinie częstotliwości odpowiada odwrotności czasu wypełniania rekordu akwizycji.

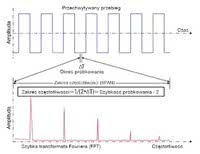
Rys. 3. Zakres częstotliwości mierzonego widma (span) równy połowie efektywnej szybkości próbkowania

Dla uzyskiwania lepszej rozdzielczości częstotliwościowej należy zwiększać liczbę danych zapisywanych w rekordzie akwizycji. W tym celu konieczne jest wydłużanie podstawy czasu (sekundy/działkę). Takie działanie powoduje jednak zmniejszenie rozdzielczości czasowej.

Jak już wiemy, długość rekordu akwizycji może być utożsamiana z czasem jego wypełniania. Czas ten jest w praktyce ustawiany pokrętłem podstawy czasu oscyloskopu. Nie trudno jednak zauważyć, że po dokonaniu tej nastawy pod kątem uzyskania wymaganej rozdzielczości częstotliwościowej (RBW) jedyną metodą osiągnięcia wymaganego zakresu częstotliwości analizy FFT (Span) jest... ustawienie odpowiedniej długości rekordu. Wydaje się to dość zawiłe, ale w praktyce nie jest aż tak trudne do opanowania.

Ostatnio obserwujemy nowy trend w implementacji interfejsu wykorzystywanego do konfigurowania funkcji FFT. Aktualnie coraz częściej przypomina on rozwiązania stosowane w prawdziwych analizatorach widma. Użytkownik ustawia więc np. częstotliwość środkową i zakres częstotliwości, mając rozdzielczość widma jako dodatkowy parametr.

Taki typ interfejsu ułatwia wprawdzie obsługę analizy FFT, lecz nie możemy zapominać, że o jej parametrach decyduje de facto kombinacja podstawy czasu, szybkości próbkowania i długości rekordu. Znając zależności pomiędzy tymi parametrami można uzyskiwać podobne rezultaty również w oscyloskopach nie mających specjalnie zaprojektowanego interfejsu funkcji FFT.

Skalowanie pionowe

Rys. 4. Składowe widma mocy przebiegu prostokątnego obliczone funkcją FFT: amplitudowa, fazowa, rzeczywista i urojona

Istnieją oscyloskopy, w których użytkownik może skalować oś pionową wykresu widmowego według własnych potrzeb oraz takie, w których przyjętego przez producenta skalowania nie można zmieniać. W analizatorach widma oś pionowa jest najczęściej skalowana w jednostkach mocy. Zwykle jest ona opisywana w dBm, czyli w jednostkach mocy zmierzonej odniesionej do 1 miliwata.

Jest to skala logarytmiczna. Takie skalowanie jest również implementowane w oscyloskopach. Przyrządy laboratoryjne posiadają również inne opcje, takie jak: PSD (Power Spectral Density - gęstość widmowa mocy), skalowanie liniowe, kwadratowe, fazowe lub zespolone (real/imaginary).

PSD jest wartością mocy widma znormalizowaną do rozdzielczości FFT. Jednostką miary jest dBm/Hz. Parametr ten odzwierciedla moc na jednostkę pasma. Pomiar PSD jest przydatny w pomiarach zjawisk szerokopasmowych, takich jak szum. Skalowanie liniowe natomiast dobrze odzwierciedla poziomy widma tak, jak mierzy je oscyloskop, a więc wyrażane w woltach lub amperach.

Wybierając skalowanie kwadratowe uzyskuje się liniową skalę mocy przy stałym obciążeniu, zwykle równym 50 Ω. Jednostką są w tym przypadku V² lub A². Oscyloskop normalizuje wyniki wykorzystując funkcję "Rescale" mnożącą bezpośredni wynik przez stałą. Dla obciążenia 50 Ω jest ona równa 0,02 (1/50). Operacja ta powoduje zamianę jednostek na waty (V²/50) dla impedancji 50 W.

Z matematycznego punktu widzenia widmo FFT jest funkcją zespoloną, a wyświetlany na ekranie wykres jest tylko połową obliczeń. Pełny wynik analizy zawiera część rzeczywistą i część urojoną. Niektóre oscyloskopy umożliwiają wyświetlenie amplitudy wraz z fazą. Pełny obraz analizy FFT składa się z dwóch par danych: rzeczywiste/urojone oraz amplituda/faza. Komponenty rzeczywiste/urojone są niezbędne do obliczania odwrotnej transformaty Fouriera.

Są one też powszechnie wykorzystywane przez mechaników, np. w pomiarach drgań, natomiast elektronicy i elektrycy korzystają najczęściej ze składowych amplituda/faza. Na rysunku 4 przedstawiono przykład pomiaru widma mocy, w którym są wyświetlane wszystkie komponenty (rzeczywiste/urojone, amplituda/faza) dla fali prostokątnej.

Oś pionowa wykresu fazowego widma jest wyskalowana w stopniach. Wykresy składowej rzeczywistej i urojonej są wyskalowane w tych samych jednostkach, które obowiązują dla kanałów pomiarowych oscyloskopu. W tym przypadku są to miliwolty. Dla sygnałów okresowych takich, jak mierzony w opisywanym eksperymencie przebieg prostokątny, znaczące wartości osiąga jedynie składowa podstawowa i jej harmoniczne.

Okienkowanie, ważenie funkcji

Rys. 5. Wpływ warunków brzegowych na kształt widma określanego funkcją FFT

Każdy oscyloskop dysponuje rekordem o określonej fizycznej długości. Parametr ten stanowi istotne ograniczenie dla implementacji funkcji FFT. W pomiarach sygnałów rzeczywistych w rekordzie akwizycji zapisywana jest zwykle nie całkowita liczba okresów. Nie ma więc mowy o ciągłości danych zapisywanych w rekordzie akwizycji. Na rysunku 5 przedstawiono jak różnice faz sygnału w punkcie początkowym i końcowym wpływają na kształt widma.

Wykresy a) i b) powstały w przypadku, gdy rekord akwizycji obejmował pełną wielokrotność okresów badanego przebiegu. Można więc mówić, że częstotliwość próbkowania jest wielokrotnością częstotliwości przebiegu. Amplituda sygnału w punkcie początkowym jest dokładnie taka sama, jak w punkcie końcowym. W rezultacie uzyskane widmo jest bardzo wąskie. Teoretycznie, dla czystego sygnału sinusoidalnego powinien to być pojedynczy prążek.

Na wykresach c) i d) w rekordzie znalazła się nie całkowita liczba okresów, a więc wartość chwilowa przebiegu w punkcie początkowym jest inna niż w punkcie końcowym. Dane zapisywane w rekordzie akwizycji nie zapewniają ciągłości czasu. Konsekwencją jest rozmycie widma FFT, a więc pojawienie się listków bocznych i jednoczesne obniżenie poziomu prążka głównego. Efekt ten jest nazywany przeciekiem. Można powiedzieć, ze energia przechwyconego sygnału przepływa pomiędzy sąsiednimi "komórkami" częstotliwościowymi (rozkłada się na nie).

Tabela 1. Charakterystyki najczęściej stosowanych w analizie FFT funkcji okna

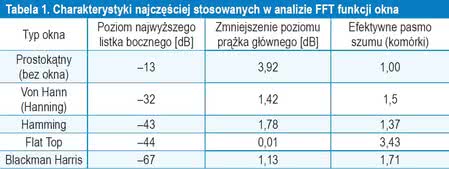
Istnieją metody minimalizowania powyższych efektów. Jest to ważenie (okienkowanie). Ważenie polega na przemnażaniu przechwyconego przebiegu przez funkcję okna tak, aby na obu krańcach danych uzyskać wartości zerowe. Od kształtu okna zależy odpowiedź widmowa, a więc linia widma i amplitudy prążków bocznych. Charakterystyki kilku najczęściej stosowanych funkcji okna przedstawiono w tabeli 1.

Rys. 6. Porównanie działania funkcji FFT dla różnych typów okien dla tego samego sygnału wejściowego

Dane zawarte w tabeli 1 charakteryzują zdolność poszczególnych okien do minimalizacji listków bocznych oraz zaniżania wysokości prążka głównego (scallop lose). Praktyczne efekty tych cech przedstawiono na rysunku 6. Widoczne na nim wykresy powstały dla tego samego sygnału wejściowego.

Wybór okna funkcji FFT powinien być dokonywany świadomie, w zależności od celu pomiaru. Jeśli mierzone mają być stany przejściowe krótsze od czasu akwizycji rekordu, nie należy stosować żadnego okna, ponieważ amplituda szczytu widma zmienia się w zależności od położenia stanu przejściowego w rekordzie akwizycji.

W tym przypadku okno prostokątne (bez ważenia) jest najlepszym wyborem. Ogólnie, okna o wąskiej odpowiedzi dają lepszą rozdzielczość częstotliwościową, natomiast okna szersze, takie jak Blackman Harris lub Flat Top należy stosować w pomiarach, w których istotna jest dokładność pomiaru amplitud. Kompromisowym rozwiązaniem może być wybór takich okien, jak Von Hann lub Hamming.

Uśrednianie w dziedzinie częstotliwości

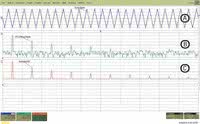
Rys. 7. Uśrednianie w dziedzinie częstotliwości poprawia stosunek sygnału do szumu zwiększając tym samym dynamikę pomiaru. W nieobrobionym widmie FFT (B) widoczne są składowe pochodzące od szumu. W widmie uśrednionym (C) składowe szumowe zanikają odsłaniając harmoniczne sygnału o niższych amplitudach

Uśrednianie jest jedną z metod poprawiania stosunku sygnału do szumu. Pomiar wymaga wykonania kilku cykli akwizycji. Uśrednianie jest prowadzone w dziedzinie czasu lub w dziedzinie częstotliwości. Sygnały asynchroniczne ze zdarzeniami wyzwalającymi, jak na przykład szum, są tłumione proporcjonalnie do liczby uśrednień. Przykład uśredniania w dziedzinie częstotliwości przedstawiono na rysunku 7.

Uśrednianie w dziedzinie częstotliwości polega na sumowaniu wartości poszczególnych komórek częstotliwościowych (każdej osobno) dla określonej liczby akwizycji, a następnie podzieleniu każdej z tak otrzymanych sum przez tę liczbę. Średnia składowych asynchronicznych widma zbliża się do zera, natomiast synchroniczne są sumowane spójnie.

Widać to dobrze na rysunku 7, gdzie składowe szumu są rozproszone po całym widmie, a mając względnie duże amplitudy dla wysokich częstotliwości skutecznie przesłaniają wyższe harmoniczne sygnału mające dużo mniejsze amplitudy. Dzięki uśrednianiu zwiększono stosunek sygnału do szumu, co spowodowało odsłonięcie wysokich harmonicznych sygnału. W analogiczny sposób redukcji ulegną wszystkie inne asynchroniczne z akwizycją składowe sygnału.

Przykład konfiguracji analizy FFT

Rys. 8. Przykładowa konfiguracja oscyloskopu do pomiaru FFT

Rozważmy pomiar widma ciągłego sygnału okresowego prowadzony oscyloskopem o paśmie 4 GHz. Ustalony arbitralnie zakres analizowanych częstotliwości powinien być równy 10 MHz, częstotliwość środkowa 2,48 GHz, a rozdzielczość częstotliwościowa 10 kHz. Na podstawie wcześniejszej dyskusji ustawienie rozdzielczości może być dokonane przez wybranie jednego parametru, jakim jest podstawa czasu (czas/działki).

Dla założonej rozdzielczości 10 kHz wymagany czas akwizycji jest równy 100 ms, co odpowiada podstawie czasu 10 ms/ dz (przy założeniu, że oś czasu ma 10 działek). Czułość pionowa oscyloskopu powinna być dobrana tak, aby sygnał zajmował co najmniej 90% całego zakresu wejściowego. Dzięki temu zakres dynamiki będzie wykorzystany maksymalnie, przy zachowaniu minimalnego, zachowanego dla bezpieczeństwa marginesu.

Zakres częstotliwości jest ustalany na podstawie szybkości próbkowania. Musi się w nim znaleźć częstotliwość środkowa 2,48 GHz, a to oznacza, że zakres częstotliwości analizowanych (span) musi być co najmniej dwukrotnie większy. Wybór częstotliwości próbkowania 5 GHz lub większej będzie odpowiedni. Maksymalna szybkość próbkowania oscyloskopu jest równa 20 GSa/s.

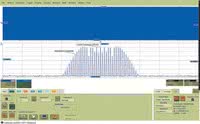
Ustawienie żądanej szybkości próbkowania może polegać na wybraniu odpowiedniej, dla przyjętej podstawy czasu, długości rekordu. Ostatecznie w wykorzystywanym oscyloskopie wybieramy rekord akwizycji o długości 1 MSa, co przy podstawie czasu 10 ms/s da wymagany czas akwizycji równy 100 ms, a szybkość próbkowania oscyloskop ustawi na 10 GSa/s. Pomiar z takimi nastawami przedstawiono na rysunku 8.

Parametry konfigurujące funkcję FFT znajdują się na zakładce "FFT" funkcji matematycznej F1. Parametry dobrano pod kątem analizy widma mocy. Ze względu na to, że badany jest sygnał ciągły, zdecydowano się na okno Von Hann'a zapewniające kompromis pomiędzy rozdzielczością częstotliwościową a dokładnością pomiaru amplitud składowych widma. Zakładka "FFT" zawiera informację o rozdzielczości częstotliwościowej (Df) równej 10 kHz, i zakresie częstotliwości 5 GHz. Elementy zakładki "Zoom" umożliwiają ustawienie częstotliwości środkowej na 2,48 GHz przy zachowaniu skali częstotliwości 1 MHz/dz, tak jak to pokazano na wykresie F1 z rysunku 8.

Podsumowanie

W artykule przedstawiono najważniejsze cechy analizy FFT, jako podstawowego narzędzia wykorzystywanego do badania widma sygnałów elektrycznych za pomocą oscyloskopów cyfrowych. Podane informacje pozwalają efektywnie wykorzystywać tę funkcję, warto o nich pamiętać wykonując pomiary.

Jarosław Doliński