Projektowanie filtrów cyfrowych

W porównaniu do filtrów analogowych filtry cyfrowe charakteryzuje szereg zalet. Jedną z nich jest łatwość uzyskania charakterystyk częstotliwościowych o w zasadzie dowolnym kształcie w pasmie przepustowym, dużym tłumieniu w pasmie zaporowym i wąskim pasmie przejściowym, które są trudno osiągalne lub nawet niemożliwe do uzyskania w wypadku filtrów analogowych. Ponadto charakterystykę filtrów cyfrowych można łatwo zmienić przez modyfikację programu.

Dlatego są one chętnie używane w zastosowaniach, które wymagają filtrowania adaptacyjnego. Polega ono na automatycznym dostosowywaniu charakterystyki filtru do zmian sygnału na wejściu, na przykład w urządzeniach telekomunikacyjnych. Jest to wymagane m.in. przy usuwaniu pogłosu, usuwaniu szumów oraz w rozpoznawaniu mowy.

Jakie są zalety i ograniczenia filtrów cyfrowych?

Kolejna zaleta filtrów cyfrowych to możliwość uzyskania liniowej charakterystyki fazowej. Dzięki temu, że do ich realizacji nie są wymagane elementy dyskretne, ich parametry nie zmieniają się w czasie w związku ze starzeniem się komponentów elektronicznych ani też pod wpływem innych czynników, na przykład zmian temperatury.

Ponadto parametry filtrów cyfrowych można dobrać precyzyjniej, ponieważ nie ma na nie wpływu tolerancja wykonania elementów dyskretnych. Zaletą filtrów cyfrowych jest również łatwiejsze projektowanie oraz symulacja. Dzięki temu projektuje się je szybciej.

Z drugiej strony, aby filtr cyfrowy spełnił swoją funkcję w zastosowaniach wymagających przetwarzania w czasie rzeczywistym, potrzebny jest procesor DSP o odpowiedniej mocy obliczeniowej. Wymagane jest bowiem, żeby zakończył wszystkie obliczenia w czasie nie dłuższym niż okres próbkowania sygnału wejściowego.

Dlatego pasmo przenoszenia filtrów cyfrowych jest ograniczone do połowy częstotliwości próbkowania. W przypadku filtrów analogowych jest ono w teorii nieograniczone.

Pasmo przenoszenia filtrów cyfrowych

Na to, jak długo mogą potrwać obliczenia, wpływa wiele czynników, m.in. liczba odczepów filtra. Każdy z nich wymaga bowiem wykonania operacji mnożenia i operacji dodawania (operacji multiply-accumulate, MAC). Dlatego procesory DSP optymalizuje się pod kątem skrócenia czasu trwania tej operacji oraz implementuje w nich dodatkowe rozwiązania przyspieszające obliczenia. Przykładem jest bufor cykliczny.

Mimo to, nawet jeżeli jedną instrukcję procesor DSP wykonuje w czasie kilku nanosekund, na przykład 5 ns, a "n" odczepów filtra wymaga wykonania "n" instrukcji, przeliczenie filtru złożonego przykładowo ze 100 odczepów potrwa 0,5 µs. Oznacza to, że maksymalna możliwa częstotliwość próbkowania będzie wynosić w tym przypadku 2 MHz. To natomiast ograniczy pasmo przenoszenia filtru zrealizowanego z wykorzystaniem procesora sygnałowego o takiej mocy obliczeniowej do 1 MHz.

Czym się różni filtr SOI od filtru NOI?

Rys. 1. Filtry cyfrowe, a) typu SOI i b) typu NOI

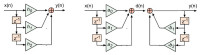
Filtry cyfrowe można podzielić na dwie grupy. Do pierwszej zaliczane są filtry o skończonej odpowiedzi impulsowej SOI (Finite Impulse Response, FIR), drugą są zaś filtry o nieskończonej odpowiedzi impulsowej NOI (Infinite Impulse Response, IIR). Ich uproszczone struktury zostały przedstawione na rysunku 1.

Wynika z niego, że filtry NOI są rekursywne, tzn. wykorzystują sprzężenie zwrotne. Próbki sygnału wyjściowego filtrów o skończonej odpowiedzi impulsowej zależą od poprzednich próbek sygnału wejściowego.

Z kolei próbki sygnału wyjściowego filtru o nieskończonej odpowiedzi impulsowej zależą od poprzednich próbek sygnału wejściowego i poprzednich próbek sygnału wyjściowego.

Filtr FIR - przykład

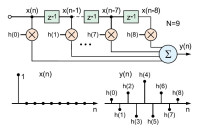
Najprostszą realizacją filtru o skończonej odpowiedzi impulsowej jest filtr z ruchomą średnią (moving average). Znajduje on zastosowanie w wygładzaniu sygnałów. Przykład tej struktury razem z zależnościami, które łączą w jej przypadku próbki sygnału wyjściowego z próbkami sygnału wejściowego, na przykładzie średniej czteropunktowej, przedstawiono na rysunku 2a. Wynika z niego, że próbki wejściowe x(n), odpowiednio opóźnione, po przemnożeniu przez 0,25, dodaje się do siebie. Wyjaśnia to dokładnie rysunek 2b.

W pierwszym kroku pierwsze cztery próbki, tj. x(0), x(1), x(2) i x(3), są zapisywane w rejestrze. Następnie wielkości te są sumowane i przemnażane przez 0,25. W ten sposób wyznaczana jest pierwsza próbka wyjściowa y(3). Następnie dodawana jest kolejna próbka wejściowa x(4), a jednocześnie odejmowana jest próbka x(0).

Kiedy nie stosować filtru z ruchomą średnią?

Rys. 2. Filtr z ruchomą średnią

Nowy wynik też jest przemnażany przez 0,25. Z powyższej analizy wynika, że by uzyskać każdą kolejną próbkę wyjściową, wykonuje się trzy operacje - sumowanie, odejmowanie i mnożenie, bez względu na to, ilu punktowa jest średnia.

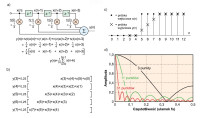
Na rysunku 2c przedstawiono odpowiedź skokową filtru z ruchomą średnią. Nie występuje w niej zjawisko overshoot, co jest przydatne wówczas, gdy trzeba odfiltrować szum biały. Na rysunku 2d przedstawiono natomiast charakterystykę częstotliwościową takiego filtru, która obrazuje, w jaki sposób liczba odczepów wpływa na skuteczność filtrowania - im jest ich więcej, tym przebieg jest bardziej stromy.

Z rysunku 2d wynika również, że z filtrów tego rodzaju lepiej nie korzystać wówczas, kiedy wymagane jest silne tłumienie w pasmie zaporowym. Można je zwiększyć, odpowiednio dobierając różne współczynniki filtru.

Jakie są zalety i wady filtrów SOI i NOI?

Zarówno filtry FIR, jak i IIR mają zalety, ale i wady. Jeżeli chodzi o te pierwsze, to do ich zalet zaliczana jest możliwość uzyskania liniowej charakterystyki fazowej, to natomiast sprawia, że wszystkie składowe sygnału są jednakowo opóźniane. Dzięki temu, że nie mają biegunów w funkcji transmitancji, ich stabilność jest pewna. Oprócz tego projektowanie filtrów SOI jest łatwiejsze niż filtrów NOI.

Z drugiej jednak strony filtry o skończonej odpowiedzi impulsowej, których charakterystyka ma spełniać specjalne wymagania, na przykład zapewniać silne tłumienie w paśmie zaporowym i strome przejście z pasma przepustowego do pasma zaporowego, wymagają dużej liczby współczynników. To z kolei zwiększa ich złożoność obliczeniową.

Jeżeli chodzi o filtry IIR, to charakteryzuje je mniejsza złożoność obliczeniowa niż filtry SOI (wymagają mniej pamięci i wykonania mniejszej liczby operacji mnożenia i dodawania). Ponadto ich algorytmy są łatwiejsze w realizacji.

Niestety, w związku z położeniem biegunów transmitancji możliwa jest utrata ich stabilności. W przypadku filtrów NOI wyższych rzędów jest ona mniej prawdopodobna, jeżeli zostaną one zrealizowane jako kaskadowe połączenie bloków filtrów drugiego rzędu.

Oprócz tego, w przeciwieństwie do filtrów FIR, nie można zrealizować filtru NOI, który miałby liniową charakterystykę fazową. Projektowanie filtrów o nieskończonej odpowiedzi impulsowej jest również trudniejsze niż projektowanie filtrów o skończonej odpowiedzi impulsowej.

Projektowanie filtrów cyfrowych

Rys. 3. Odpowiedź impulsowa filtru FIR

Kolejne kroki procedury projektowania filtru cyfrowego są podobne do tych, które wykonuje się, projektując filtr analogowy. Najpierw należy doprecyzować wymagania stawiane filtrowi przez określenie żądanej charakterystyki amplitudowo-fazowej, a następnie zaprojektować strukturę filtru, która pozwoli je spełnić.

W uproszczeniu główna różnica między filtrami analogowymi a cyfrowymi polega na tym, że w przypadku tych drugich, zamiast wyznaczać wartości rezystorów, kondensatorów i cewek, trzeba wyznaczyć właściwą liczbę odczepów i wartości współczynników filtru.

Założenie, które jest podstawą wszystkich metod projektowania filtrów ze skończoną odpowiedzią impulsową, wyjaśnia rysunek 3. Wynika z niego, że po podaniu na wejście filtru FIR sygnału impulsowego sygnałem wyjściowym filtru jest zbiór jego współczynników. W związku z tym projektowanie filtrów SOI polega w uproszczeniu na wyznaczeniu odpowiedzi impulsowej na podstawie wymaganej charakterystyki częstotliwościowej filtru, a potem kwantyzacji tej pierwszej w celu wyznaczenia jego współczynników. W praktyce filtry o skończonej odpowiedzi impulsowej projektuje się, wykorzystując kilka technik.

Projektowanie filtrów SOI

Rys. 4. Etapy projektowania filtrów FIR metodą okien czasowych

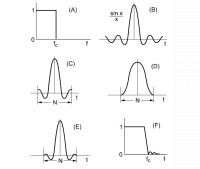
Na rysunku 4 przedstawiono kolejne etapy projektowania filtru FIR metodą okien czasowych. Przebieg na rysunku 4a jest charakterystyką częstotliwościową idealnego filtru dolnoprzepustowego. Na rysunku 4b przedstawiono jego odpowiedź impulsową, która ma postać funkcji sin(x)/x.

W kolejnym kroku obcina się ją tak, aby uzyskać możliwą do realizacji liczbę odczepów N (rys. 4c). W celu likwidacji nieciągłości zakończeń otrzymanego przebiegu, które miałyby niekorzystny wpływ na parametry filtru, wykorzystuje się funkcję okna (rys. 4d), przez którą mnoży się odpowiedź impulsową, otrzymując przebieg z rysunku 4e. Wybór okna czasowego ma wpływ na parametry filtru. Rysunek 4f przedstawia charakterystykę częstotliwościową zaprojektowanego w ten sposób filtru FIR.

W kolejnej metodzie należy zdefiniować funkcję H(f) i rozwinąć ją w szereg Fouriera. W ten sposób wyznacza się współczynniki filtru. Podobnie jak w pierwszym sposobie, odpowiedź impulsową kształtuje się przez zastosowanie odpowiedniej funkcji okna. Wadą tej metody jest trudność w uzyskaniu z dużą dokładnością wymaganych parametrów filtru. Ograniczenie to szczególnie dotyczy częstotliwości granicznej.

W programach komputerowych wspomagających projektowanie filtrów cyfrowych często implementuje się również algorytm Parksa-McClellana. Ten z kolei opiera się na twierdzeniu Remeza. Jedna z takich aplikacji zostanie przedstawiona dalej.

Projektowanie filtrów NOI

Filtry o skończonej odpowiedzi impulsowej nie mają odpowiedników analogowych. Inaczej jest w przypadku filtrów o nieskończonej odpowiedzi impulsowej. Dzięki temu można je projektować z wykorzystaniem bardziej tradycyjnych technik.

Wyróżnić można trzy najczęściej wykorzystywane sposoby projektowania filtrów IIR. Są to metody: niezmienności odpowiedzi impulsowej (impulse invariance), transformacji biliniowej (bilinear transform) oraz optymalizacji (optimizatiton method). Dalej szerzej omawiamy drugą z nich.

W metodzie transformacji biliniowej można wyróżnić kilka etapów. W pierwszym z nich należy wyznaczyć funkcję transmitancji H(s) dla analogowego prototypu filtru. Najpopularniejsze filtry analogowe to filtry typu: Butterwortha, Czebyszewa, eliptyczne oraz Bessela. Wyróżniającą cechą filtrów Butterwortha jest maksymalnie płaska charakterystyka amplitudowa w paśmie przenoszenia. Jeżeli zaś chodzi o filtry Czebyszewa, to wyróżnia się dwa ich rodzaje.

Charakterystyczną cechą filtrów Czebyszewa pierwszego typu są zafalowania w przebiegu charakterystyki amplitudowej w paśmie przepustowym i płaski przebieg tej charakterystyki w paśmie zaporowym. W porównaniu do filtrów Butterwortha filtry Czebyszewa pierwszego typu mają węższe pasmo przejściowe przy takiej samej liczbie biegunów transmitancji.

Metoda transformacji biliniowej

Filtry Czebyszewa drugiego typu mają z kolei zafalowania w przebiegu charakterystyki amplitudowej w paśmie zaporowym oraz płaski przebieg tej charakterystyki w paśmie przepustowym. Są one rzadziej używane niż filtry Czebyszewa pierwszego typu.

Filtry eliptycznie (Cauera) mają zafalowania w przebiegu charakterystyki amplitudowej zarówno w paśmie przepustowym, jak i w paśmie zaporowym. W porównaniu do filtrów Czebyszewa o takiej samej liczbie biegunów transmitancji wyróżnia je jeszcze węższe pasmo przejściowe. Wadą filtrów eliptycznych jest duża nieliniowość charakterystyki fazowej.

Filtry Bessela (Thompsona) mają z kolei wyjątkowo płaską charakterystykę fazową. W porównaniu do innych filtrów przy tej samej liczbie biegunów transmitancji mają najmniejszą stromość charakterystyki amplitudowej. W przebiegu tej ostatniej nie występują zafalowania.

W metodzie transformacji biliniowej płaszczyzna s na płaszczyznę z zostaje odwzorowana za pomocą przekształcenia dwuliniowego (biliniowego). W związku z tym kolejnym etapem, po wcześniejszym określeniu częstotliwości próbkowania fs filtru cyfrowego oraz wyznaczeniu odstępu próbkowania ts, jest podstawienie w miejsce zmiennej s w transmitancji H(s) wyrażenia:

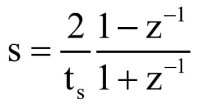
Następnie otrzymaną w ten sposób zależność należy przekształcić do postaci:

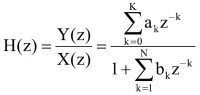
Programy wspomagające projektowanie filtrów cyfrowych

Rys. 5. ScopeFIR

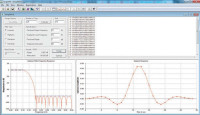
Dostępnych jest wiele programów wspomagających projektowanie filtrów cyfrowych. Przykładem są Scope-FIR oraz ScopeIIR firmy Iowegian International. Na stronie internetowej tego producenta (www.iowegian.com) udostępniono bezpłatną 30-dniową wersję testową tych programów.

ScopeFIR to narzędzie do projektowania filtrów SOI kilkoma metodami. Pracę z programem rozpoczyna utworzenie nowego projektu. Do wyboru są następujące opcje: simple Parks-McClellan, advanced Parks-McClellan, windowed sinc, raised cosine, lth-band (Nyquist), import/boxcar, maximally flat oraz CIC.

W pierwszych dwóch do obliczeń wykorzystywany jest algorytm Parksa-McClellana, a w trzecim metoda okien. Kolejna opcja służy do projektowania filtrów FIR o charakterystyce podniesionego kosinusa i pierwiastka z podniesionego kosinusa. Ten typ filtrów często jest wykorzystywany w telekomunikacji m.in. do usuwania skutków interferencji międzysymbolowych. Następna opcja pozwala zaprojektować tzw. filtr Nyquista.

Wybierając "Import/Boxcar", możemy zaimportować projekt filtru wykonany poza programem ScopeFIR albo zaprojektować prosty filtr typu "boxcar", czyli ze wszystkimi współczynnikami równymi 1. Kolejna opcja pozwala projektować filtry specjalnej klasy o maksymalnie płaskiej charakterystyce, a ostatnia filtry typu CIC (cascaded integrated-comb), nazywane też filtrami Hogenauera. Filtry te często wykorzystuje się w sprzętowej implementacji decymatorów i interpolatorów.

Jak zaprojektować filtr w ScopeFIR?

W metodzie Parksa-McClellana użytkownik powinien określić częstotliwość próbkowania (sampling frequency) i podać liczbę odczepów (number of taps), o ile ma pod tym względem konkretne oczekiwania. W przeciwnym wypadku do tego punktu trzeba wrócić po określeniu innych parametrów. W testowej wersji programu maksymalna liczba odczepów to 32.

Należy też podać gęstość siatki (grid density), parametr wykorzystywany w obliczeniach filtru. Domyślna wartość 16 wystarczy w większości przypadków. Jeżeli użytkownik uzna, że wyniki obliczeń nie spełniają założeń projektu, może ten parametr zwiększyć, pamiętając, że im większa będzie gęstość siatki, tym dłużej potrwają obliczenia.

Trzeba też określić typ filtru (filter type): DP, GP, pasmowo-zaporowy lub pasmowo-przepustowy. W zależności od typu filtru podać należy górną, dolną albo obie częstotliwości odcięcia, a także dopuszczalne tętnienia w pasmie przepustowym filtru (passband ripple) oraz tłumienie w pasmie zaporowym (stopband attenuation).

Następnie można wyznaczyć liczbę odczepów filtru, wybierając przycisk estimate w sekcji numbers of taps. Opcja ta jest dostępna tylko w przypadku filtrów DP i GP. Obliczenia uruchamia przycisk design albo optimize.

W dolnym oknie wyświetlane są charakterystyki zaprojektowanego filtru: częstotliwościowa oraz odpowiedź impulsowa, natomiast w górnej części - współczynniki filtru. Inne charakterystyki można obejrzeć, korzystając z opcji view w menu. Jeżeli wyniki nie spełniają założeń projektu, trzeba zwiększyć lub zmniejszyć liczbę odczepów filtru i obliczenia powtórzyć.

Jak korzystać ze ScopeIIR i TFilter?

Rys. 6. TFilter

ScopeIIR to program do projektowania filtrów o nieskończonej odpowiedzi impulsowej na podstawie prototypu analogowego filtru Butterwortha, Czebyszewa albo eliptycznego. Po uruchomieniu aplikacji widoczne jest okno, w którym użytkownik może wprowadzić dane niezbędne do obliczeń.

Podać trzeba: typ filtru, częstotliwość próbkowania, rząd filtru (w wersji testowej maks. 4), częstotliwości odcięcia, dopuszczalne tętnienia w pasmie przepustowym, tłumienie w pasmie zaporowym, wzmocnienie oraz oczekiwaną dokładność, z jaką wyznaczane będą współczynniki filtru. Do uruchomienia obliczeń służy przycisk design.

Jeżeli zaznaczona jest opcja automatic, wyniki będą automatycznie aktualizowane w razie zmiany przez użytkownika któregokolwiek z parametrów wejściowych. Obok panelu do wprowadzania danych wejściowych prezentowane są charakterystyki zaprojektowanego filtru.

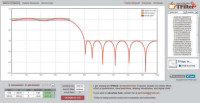
W Internecie można również znaleźć wiele całkowicie darmowych aplikacji online to projektowania filtrów cyfrowych. Przykładem jest TFilter, dostępna na stronie pod adresem http://t-filter.engineerjs.com.

Służy ona do projektowania filtrów FIR z wykorzystaniem algorytmu Parksa-McClellana.

Aby z niej skorzystać, należy podać częstotliwość próbkowania i wymaganą liczbę odczepów filtru oraz opisać jego pasmo przenoszenia i tłumienia (from, to, gain, ripple/att.). Obliczenia uruchamia przycisk design filter.

Po ich zakończeniu w głównym oknie aplikacji TFilter wyświetlona zostaje charakterystyka amplitudowa filtru, a w prawej części okna - lista obliczonych współczynników. Domyślnie są one prezentowane jako tekst (plain text), ale można także zmienić ich format na C/C++ array. Wówczas jest przygotowywany fragment kodu definiujący tablicę współczynników filtru. Możliwa jest również zmiana precyzji współczynników, z double na int.

W oknie głównym aplikacji poza wykresem Gain vs. Frequency dostępna jest też zakładka, w której wyświetlana jest odpowiedź impulsowa filtru (Impulse response) oraz zakładka Source Code. W tej drugiej znaleźć można implementacje zaprojektowanego filtru SOI w językach C oraz C++.

Monika Jaworowska