Analiza szumów w filtrach analogowych i cyfrowych

Filtry analogowe

Rys. 1. Prosty filtr dolnoprzepustowy

Pasmo przenoszenia szumów w filtrach pasmowych i dolnoprzepustowych zależy głównie od odpowiedzi filtra. Dla filtrów górnoprzepustowych i pasmowozaporowych szumy zależą jednak przeważnie od pasma zastosowanego wzmacniacza. Wiele wzmacniaczy operacyjnych jest źródłem nie tylko szumu napięciowego, ale również szumu prądowego.

Impedancja znajdująca się na wejściu wzmacniacza filtra wprowadza szum prądowy oraz szum napięciowy. Ich wartość zależy od konkretnej topologii, od impedancji pozornych w obwodach RC wzmacniacza oraz od wartości rezystorów i kondensatorów. Szumy można analizować na dwa sposoby.

Pierwsze podejście zakłada, że jedynym źródłem szumów w obwodzie jest szum Johnsona w rezystorach, a kondensatory są bezszumowe. Niniejsza metoda jest wykorzystywana przez program SPICE, który oblicza wartość szumu Johnsona każdego rezystora, podnosi do kwadratu i sumuje.

Rys. 2. Odpowiedź filtra dolnoprzepustowego dla krokowej zmiany częstotliwości odcięcia

Pierwiastek kwadratowy z otrzymanej sumy jest wartością skuteczną całkowitego napięcia szumów. Istnieją jednak sytuacje, gdy konieczne staje się założenie rezystancji dążącej do nieskończoności. Ponieważ gęstość napięcia szumów Johnsona jest proporcjonalna do pierwiastka kwadratowego rezystancji, problematyczne staje się nieskończone napięcie szumów rezystora o nieskończonej rezystancji.

Dlatego istnieje również druga metoda analizy, często stosowana przez projektantów układów scalonych, w której analizuje się kondensatory, a rezystory są pomijane. Częstym sposobem jej realizacji jest rozważenie napięcia szumów równoległego połączenia rezystora i kondensatora.

Całkowite napięcie szumów jest iloczynem dwóch składowych: gęstości napięcia szumów proporcjonalnej do √R oraz pierwiastka kwadratowego pasma pomiarowego, który jest proporcjonalny do 1/√RC. Zatem szum całkowity jest proporcjonalny do 1/√(C) i nie zależy od wartości rezystora. Wraz ze zmianą rezystancji zmienia się gęstość widmowa szumu, jednak wartość szumu pozostaje stała.

Rys. 3. Zależność gęstości szumów od częstotliwości odcięcia przy równych wartościach skutecznych

Nie oznacza to jednak, że źródłem szumów są kondensatory. Resztkowa niepewność napięcia kondensatora połączonego równolegle z rezystorem o nieskończonej rezystancji (ich kombinacja ma zatem zerowe pasmo) jest wskaźnikiem wartości szumu Johnsona z chwili wcześniejszej. Oznacza to, że kondensator przechowuje wartość szumu termicznego rezystora obwodu, który naładował kondensator.

Takie zachowanie jest generalizacją każdego układu RC, także aktywnego. Gdyby utrzymać na stałym poziomie pojemność kondensatora filtru aktywnego i przeskalować rezystory o stałą wartość w celu zmiany częstotliwości odcięcia, to całkowity szum obwodu pasywnego pozostanie stały.

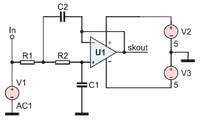
Można to łatwo wykazać w symulacji. Na rysunku 1 przedstawiono prosty filtr dolnoprzepustowy Sallen-Key (2. rzędu Butterwortha), którego parametry są obliczane dla różnych częstotliwości odcięcia. Pojemność uziemionego kondensatora jest stała i wynosi 100 nF, a wartość kondensatora górnego 200 nF.

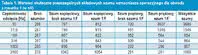
Tabela 1. Wartości skuteczne poszczególnych składowych szumu wzmacniacza operacyjnego dla obwodu z rysunku 1 (w nV)

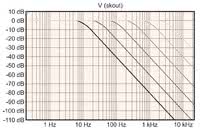
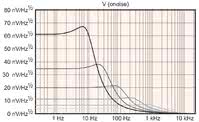
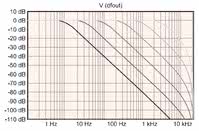
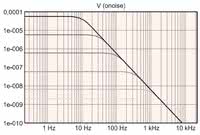
Wartości rezystorów R1 i R2 są obliczane dla krokowych zmian częstotliwości, a pojemności kondensatorów pozostają stałe. Na rysunku 2 pokazano odpowiedź filtra dla częstotliwości odcięcia od 10 Hz do 3160 Hz. Rysunek 3 przedstawia zależność gęstości szumów od częstotliwości przy użyciu bezszumowego wzmacniacza.

Wartość skuteczna szumów wynosi w każdym przypadku 287 nV dla testowego pasma między 0,2205 Hz a 22050 Hz. Utrzymywanie stałych rezystorów i zmiana wartości kondensatorów zmienia całkowitą wartość szumu.

Rys. 4. Wartości skuteczne składowych szumu (w nV)

Dlatego bardziej fundamentalną metodą sterowania częstotliwością odcięcia filtra jest skalowanie rezystorów przez stałą i utrzymanie pojemności kondensatorów na stałym poziomie. Wiedza o konkretnej wartości szumu pozwala na zmniejszenie liczby rozważanych zmiennych o jeden.

Kwestia staje się bardziej skomplikowana w przypadku wzmacniacza rzeczywistego, który ma własny szum napięciowy i prądowy. Każda składowa na swój sposób wpływa na całkowity szum. Szum napięciowy wprowadzany przez wzmacniacz rośnie wraz z pierwiastkiem pasma szumów i w konsekwencji jest proporcjonalny do częstotliwości odcięcia filtra.

Jednocześnie szum prądowy na wejściach wzmacniacza generuje odpowiadający mu szum napięciowy, proporcjonalny do wartości impedancji i odwrotnie proporcjonalny do częstotliwości odcięcia. Zatem wkład tego szumu rośnie wraz ze spadkiem częstotliwości odcięcia.

Rys. 5. Badany filtr o strukturze bezpośredniej

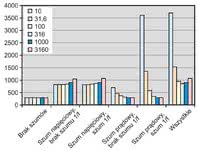
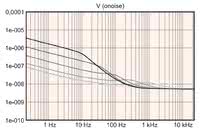
Obecność szumu 1/f w składowej prądowej i napięciowej dodatkowo zwiększa złożoność sytuacji. W tabeli 1 pokazano łączne wartości szumów na wyjściu filtra otrzymane z symulacji. Wyniki z tabeli 1 zostały przedstawione na rysunku 4 w postaci wykresu słupkowego, który pozwala zauważyć charakter zmian szumów napięciowych i prądowych wraz ze wzrostem częstotliwości odcięcia.

Widoczny jest również dominujący wkład szumu 1/f w składowej prądowej dla niskich częstotliwości. Ponadto widać, że istnieje pewna częstotliwość odcięcia, przy której wartość skuteczna całkowitego napięcia szumów będzie minimalna. Poziom szumów w rzeczywistych wzmacniaczach jest wyższy niż w idealnych, jednak wciąż dość łatwo ustalić jego wartość.

Filtry cyfrowe

Rys. 6. Filtr o strukturze bezpośredniej utworzony z bloków SPICE

Jednak czy można dokładnie ustalić, jaki będzie szum filtra zaimplementowanego cyfrowo? W przypadku przetwarzania analogowego filtrowanie oraz inne operacje są wykonywane przed ewentualną konwersją sygnału do postaci cyfrowej.

Model cyfrowy wymaga natomiast jak najszybszego przekształcenia sygnału do postaci cyfrowej, przetworzenia go w tej dziedzinie i ewentualnego przekształcenia z powrotem do formy analogowej.

Na przykład układ PSoC3 produkcji firmy Cypress zawiera wzmacniacze operacyjne do tworzenia aktywnych filtrów analogowych oraz umożliwia implementację wielu filtrów w dziedzinie cyfrowej.

Aby wybrać odpowiedni filtr, niezbędne jest opracowanie metody, która umożliwi rzetelne porównanie szumów filtrów analogowych i cyfrowych. W dziedzinie cyfrowej każda próbka jest obarczona błędem kwantyzacji, który wynika z dopasowania wartości o wysokiej precyzji do systemu o niższej rozdzielczości, zwykle N-bitowego systemu binarnego o 2N dostępnych stanach.

Rys. 7. Schemat do symulacji szumu standardowego filtra dwukwadratowego o strukturze bezpośredniej

Dla dowolnego sygnału rzeczywistego niniejszy błąd jest całkowicie nieskorelowany z bieżącą wartością sygnału i dlatego może być traktowany jako szum losowy, którego wartość jest jednolicie rozłożona między ±0,5 LSB.

Taki szum określa się w podręcznikach jako szum biały, tj. jego gęstość widmowa nie zależy od częstotliwości, a wartość średniokwadratowa między DC a częstotliwością Nyquista wynosi LSB/√(12). Błąd kwantyzacji różni się od szumu analogowego w szczególny sposób: jest deterministyczny. Wynikiem przetworzenia identycznego sygnału po raz kolejny będzie taki sam błąd.

Natomiast w układzie analogowym szum jest inny za każdym razem. Aby stworzyć takie same warunki do porównania filtrów analogowych z cyfrowymi, zakładamy, że sygnały wejściowe są przetwarzane na cyfrowe, po filtrze analogowym lub przed filtrem cyfrowym, z użyciem wystarczającej liczby bitów rozdzielczości, która pozwoli na pominięcie wejściowego błędu kwantyzacji.

Rys. 8. Schemat filtra analogowego i cyfrowego

Sygnał 20-bitowy będzie przetwarzany na 24-bitowej jednostce arytmetycznej, której rozdzielczość odpowiada szerokości drogi sygnałowej filtra PSoC3. Nie zachodzi zatem wewnętrzna redukcja rozdzielczości, która mogłaby wpłynąć na wynik.

Ponieważ filtry cyfrowe nie zawierają powodujących szumy wzmacniaczy operacyjnych oraz komponentów pasywnych, to czy po uniknięciu błędu kwantyzacji filtr cyfrowy nie powinien być idealny i bezszumowy?

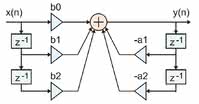
Niestety najczęściej stosowany filtr, którym jest przedstawiony na rysunku 5 filtr o strukturze bezpośredniej, będący standardem w większości podręczników i pakietów oprogramowania do projektowania filtrów, ma również inne źródła szumów. Pierwszym etapem w procesie ich ustalania jest znalezienie sposobu analizy obwodu.

Rys. 9. Odpowiedź cyfrowego filtra dolnoprzepustowego dla krokowych zmian częstotliwości odcięcia

Podobnie jak wiele innych filtrów cyfrowych, filtr o strukturze bezpośredniej składa się z jednostkowych opóźnień równych częstotliwości próbkowania. Taki obwód jest łatwy do analizy w programie SPICE, ponieważ opóźnienie można zamodelować blokiem linii przesyłowej, która ma płaską odpowiedź częstotliwościową oraz stałą wartość opóźnienia grupowego i fazowego.

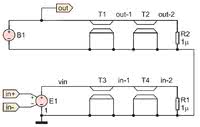
Na rysunku 6 pokazano schemat filtra utworzony z podstawowych bloków SPICE oraz węzła sumacyjnego. Na tym etapie napięcie wyjściowe jest obliczane w postaci liczby zmiennoprzecinkowej. Do modelowania rzeczywistej implementacji konieczne jest jednak uwzględnienie 24-bitowego kwantyzatora, którego można będzie użyć w liniowej analizie SPICE.

Ponieważ błąd kwantyzacji w obwodzie cyfrowego przetwarzania sygnału można rozpatrywać jako szum biały, możliwe jest zastąpienie go generatorem szumu białego o takiej samej wartości skutecznej amplitudy oraz gęstości widmowej szumów.

Rys. 10. Gęstość widmowa szumu filtra analogowego

Do tego celu można użyć standardowego odpowiednika SPICE - rezystora, bez wpływu na amplitudę oraz właściwości widmowe wyjściowego szumu układu. Użycie rezystora pozwoli oszacować wpływ kwantyzatora w tej samej symulacji, która służy do analizy szumu filtra analogowego.

Aby ustalić wymaganą wartość rezystora, należy przekształcić równanie wpływu rezystancji na wartość skuteczną napięcia szumów dla pasma Δf:

V_rms = √(4•k•T•R•Δf)

gdzie: T - temperatura bezwzględna, k - stała Boltzmanna. Po zdefiniowaniu maksymalnej amplitudy układu jako jednostkowej, wartość skuteczna napięcia szumów pochodzących od kwantyzatora będzie opisana równaniem:

V = 2^-bitów/√(12)

Po podniesieniu do kwadratu i porównaniu otrzymujemy:

R = 2^-bitów/(48•k•T•Δf)

lub

R = 2^-bitów/(24•k•T•F)

po podstawieniu połowy częstotliwości próbkowania za Δf. Zatem kwantyzator można sprowadzić do rezystora o wartości zależnej od częstotliwości próbkowania oraz liczby bitów rozdzielczości. Rezystor został umieszczony szeregowo z kwantyzowanym sygnałem i jest buforowany źródłem o stabilizowanym napięciu, aby uniknąć oddziaływania z resztą obwodu.

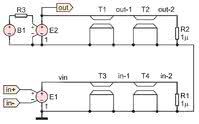
Zmodyfikowany obwód filtra pokazano na rysunku 7. Linia transmisyjna SPICE ma określoną impedancję terminacji. Aby zapewnić, że impedancja ta nie wpłynie na obliczenia szumów, została w symulacjach ustawiona na wartość 1 μΩ. Obliczona rezystancja, będąca ekwiwalentem szumów 24-bitowego kwantyzatora, wynosi około 0,81 Ω dla częstotliwości próbkowania 44,1 kHz.

Porównanie

Na rysunku 8 przedstawiono schemat omówionego wcześniej filtra analogowego, a także filtra cyfrowego, który dla uproszczenia został ukryty w małym symbolu. Na rysunku 9 pokazano odpowiedzi częstotliwościowe filtra cyfrowego dla pasma od 10 do 3160 Hz, analogicznego jak przy analizie filtra analogowego.

Odpowiedź wszystkich filtrów cyfrowych opada gwałtowniej wraz ze zbliżaniem się do częstotliwości Nyquista (22,05 kHz), co jest produktem ubocznym zastosowania biliniowej transformaty w procesie projektowania. Na rysunkach 10 i 11 przedstawiono wyniki analizy szumów, a łączne wartości liczbowe podano w tabeli 2.

Wnioski

Rys. 11. Gęstość widmowa szumu filtra cyfrowego

Analiza pokazuje, że przekonanie o wyższości filtrów cyfrowych nad analogowymi w każdym przypadku jest mocno przesadzone. Wyniki powinny raz na zawsze rozwiać mit, że szumy w filtrach cyfrowych nie istnieją. Nawet przy 24 bitach rozdzielczości filtr o strukturze bezpośredniej okazał się gorszy od filtra analogowego dla częstotliwości niższych niż 300 Hz.

Dla częstotliwości odcięcia 10 Hz szumy filtra cyfrowego były większe o 34 dB niż dla jego analogowego odpowiednika. Widać wyraźnie, że w niskich częstotliwościach filtr aktywny znacznie przewyższa wydajnością ten konkretny filtr cyfrowy.

Skąd zatem biorą się szumy w filtrze cyfrowym? Ich źródłem jest kwantyzator, a filtr o strukturze bezpośredniej znacznie je wzmacnia, nawet o współczynnik dążący do nieskończoności przy częstotliwości bliskiej zeru.

W niskich częstotliwościach odcięcia składowe sprzężenia zwrotnego filtra tworzą sprzężenie dodatnie zwiększające wzmocnienie, a sygnał wejściowy jest tłumiony przez składowe sprzężenia wyprzedzającego. Skutkiem jest duże wzmocnienie szumu na wyjściu filtra wynikające z działania nieodłącznego kwantyzatora.

Jednym ze sposobów zmniejszenia szumów jest zwiększenie rozdzielczości operacji arytmetycznych. Zbliżoną wydajność filtra analogowego i cyfrowego dla częstotliwości 10 Hz można uzyskać po rozszerzeniu pasma z 24 do 30 bitów.

Tabela 2. Wartości skuteczne szumu filtra analogowego i cyfrowego otrzymane z symulacji dla jednakowych częstotliwości odcięcia

Może to być wykonalne i uzasadnione w przypadku projektowania własnego układu od podstaw, jednak jest rzadkością, gdyż z reguły wykorzystuje się standardowy procesor. Filtry cyfrowe nie stoją jednak na straconej pozycji.

Do budowy dobrego filtra IIR m.cz. na pasmo audio można wykorzystać inne topologie, które nie wzmacniają szumów jak filtr o strukturze bezpośredniej oraz charakteryzują się znacznie lepszą wydajnością szumową dla danej szerokości pasma.

Przy stosowaniu filtrów o strukturze bezpośredniej w niskich częstotliwościach odcięcia w stosunku do częstotliwości próbkowania należy zachowywać czujność lub dalej używać filtrów analogowych.

Grzegorz Michałowski