Suma kontrolna CRC - jak ją efektywnie wyznaczyć, aby uniknąć błędów?

Suma kontrolna CRC - jak działa?

Jedną z najbardziej popularnych metod wykorzystywanych do wykrywania błędów w zbiorach danych jest suma kontrolna CRC (Cyclic Redundancy Check). Jest to rodzina kodów przeznaczonych do zapewniania integralności danych cyfrowych. Pozwala wykryć błędy wynikające z istnienia szumów kanału (przekłamanie bitu) lub zaniku sygnału (utraty jednego lub więcej bitów). Kod taki generuje pewną liczbę dodatkowych bitów, które są dodawane do przesyłanej wiadomości. Odbiornik oblicza ponownie sumę kontrolną CRC na podstawie przesłanych danych i porównuje wynik obliczeń z sumą zawartą w wiadomości. Równość obu sum świadczy o braku błędów w otrzymanym strumieniu. Mechanizm CRC jest powszechnie wykorzystywany w cyfrowej komunikacji oraz w komputerowych systemach gromadzenia danych (np. napędy HDD).

Suma kontrolna CRC powstaje w wyniku operacji binarnego dzielenia wielomianów, jakie tworzy wiadomość oraz wielomian generatora. Operacja dzielenia jest zazwyczaj implementowana w formie liniowych rejestrów przesuwających ze sprzężeniem zwrotnym – LFSR (Linear Feedback Shift Register). Każdy stan takiego rejestru stanowi liniową kombinację stanu poprzedniego oraz bitu pobieranego z wiadomości. Operacje liniowe są realizowane jako funkcje logiczne XOR i AND.

Pomimo deterministycznego charakteru operacji na rejestrach LFSR i przeznaczenia na sumę kontrolną mniejszej liczby bitów niż na wiadomość, możliwe jest jednoznaczne stwierdzenie, czy odebrana wiadomość zawiera błędy. Wyznaczanie CRC w systemach typu embedded wymaga zastosowania metody w minimalnym stopniu wykorzystującej zasoby systemowe, czyli pamięć operacyjną i moc obliczeniową. W niniejszym artykule poruszone zostały aspekty teoretyczne i praktyczne wyznaczania sumy CRC, zilustrowane na przykładzie mikroprocesora Blackfin firmy Analog Devices. Podstawowym celem jest tu opracowanie efektywnego rejestru LFSR, natomiast dodatkowo poruszono kwestię konwersji struktury wewnętrznej rejestru na strukturę zewnętrzną.

Metody

Wyznaczanie sum kontrolnych CRC odbywa się w ciele Galois (GF – Galois Field). Jest to przestrzeń liczbowa GF(2) zawierająca dwa symbole elementarne: 0 oraz 1. Dodatkowo zdefi niowane są tu dwie operacje: + oznaczająca sumę modulo- 2 (czyli XOR) oraz * oznaczająca iloczyn logiczny (AND).

Przyjmując, że przesyłana wiadomość M jest złożona z k bitów, natomiast wyznaczona suma kontrolna CRC jest złożona z n bitów, można zdefiniować następujące wielomiany:

Suma kontrolna CRC jest tu zdefiniowana jako C_n-1(x)={M_k-1(x)*xⁿ} mod G_n(x). Operacja mod jest wykonywana jako suma modulo-2 w przestrzeni GF(2). Jak wspomniano wcześniej, operacje te mogą zostać wykonane za pomocą rejestru liniowego LFSR przyjmującego jedną z dwóch form.

Listing. Przykład programu wykorzystującego instrukcje BXOR oraz BXORSHIFT

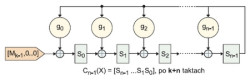
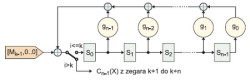
W pierwszej z nich, zwanej zewnętrzną (inne określenia to Typ I lub rejestr LFSR Fibonacciego), występują bramki XOR dołączone do poszczególnych sekcji rejestru i umieszczone w ścieżce sprzężenia zwrotnego. Dane pobierane z poszczególnych sekcji są dodawane modulo 2 i wprowadzane ponownie do rejestru od strony najmniej znaczącego bitu (LSB). Druga forma rejestru LFSR nosi nazwę wewnętrznej (typu II lub Galois). Bit sprzężenia zwrotnego jest tu pobierany z najbardziej znaczącej pozycji rejestru (MSB), a następnie wprowadzany do wybranych sekcji rejestru poprzez dołączone do nich bramki XOR. Ta forma rejestru LFSR jest popularniejsza, gdyż wydaje się być wydajniejszą, po zaimplementowaniu z użyciem sprzętowych bramek logicznych. Obie metody wyznaczania sum CRC (algebraiczna i rejestrowa) mają cechy wspólne, jednakże niewielu projektantów zdaje sobie sprawę z faktu, że obie formy rejestru LFSR są równoważne. Schematyczna budowa rejestru LFSR typu II została przedstawiona na rysunku 1, natomiast typu I – na rysunku 2. Konwersję typu rejestru z wewnętrznego na zewnętrzny można dokonać na dwa sposoby:

W obu przypadkach wyznaczanie CRC z wiadomości M rozpoczyna się od najbardziej znaczącego bitu M_k-1. Przykładowy wielomian do wyznaczania CRC może mieć postać G₅(x)=X⁵+ X⁴+ X² + 1. Jego implementacja w formie zewnętrznej i wewnętrznej została przedstawiona na rysunkach odpowiednio 3 i 4. Warto zauważyć, że podając na wejścia obu tych realizacji identyczny strumień bitów, uzyskamy identyczny rezultat, czyli wyznaczoną sumę CRC.

Rys. 1. Budowa rejestru liniowego LFSR typu I lub Fibonacciego		Rys. 2. Rejestr LFSR o strukturze wewnętrznej (typu II lub Galois)

Inicjacja rejestru LFSR

W praktyce spotyka się kilka sposobów implementacji sumy CRC różniących się m. in. kolejnością pobierania bitów z wiadomości, stosowaniem bądź nie ich negacji oraz początkową wartością rejestru LFSR. Niektóre standardy wymagają wstępnego wyzerowania rejestru, natomiast inne zalecają wypełnienie go w całości jedynkami logicznymi. Ogólnie każdy stan początkowy jest dopuszczalny. Mając podaną wartość inicjującą dla rejestru typu wewnętrznego, koniecznie trzeba opracować metody jej konwersji na wartość odpowiadającą rejestrowi zewnętrznemu.

Poszukiwanie rozwiązania tego problemu warto rozpocząć od założenia, że dana jest wartość I_n określająca stan początkowy rejestru LFSR typu wewnętrznego. Wartość CRC po k+n iteracjach będzie identyczna, jak dla rejestru LFSR zainicjowanego samymi zerami. Wynika to z faktu, że pierwszych n bitów jest przesuwanych w rejestrze bez sprzężenia zwrotnego. Po tych n iteracjach rejestr zawiera wartość I_n i wiadomość zaczyna oddziaływać na sprzężenie zwrotne. Wiedząc, że oba typy rejestrów LFSR są równoważne, po zainicjowaniu zerami można powtórzyć to samo działanie dla rejestru zewnętrznego. W tym przypadku po n iteracjach poszczególne komórki rejestru mają wartości wynikające z zastosowanego wielomianu generatora. Istnieje możliwość wyznaczenia tej wartości i zastosowanie jej do inicjacji. Trzymając się podanego wcześniej przykładu G₅(x)=X⁵+X⁴+ X²+ 1, można następująco przedstawić to działanie. Zakładając, że rejestr typu wewnętrznego został zainicjowany wartością [00000], możliwe jest wykonanie kolejnych kroków, aby określić stan początkowy rejestru typu zewnętrznego.

Należy wprowadzić do LFSR liczbę [11111] i otrzymany rezultat wykorzystać do inicjacji rejestru typu zewnętrznego. Kolejne iteracje wyglądają następująco: [00000] → [10000] → [01000] → [10100] → [11010] → [01101]. Zewnętrzny rejestr LFSR zainicjowany otrzymaną wartością da w efekcie taką samą wartość jak rejestr wewnętrzny zainicjowany wartością [11111].

Rys. 3. Implementacja przykładowego wielomianu G5=X5+ X4+ X2 + 1 w formie zewnętrznej		Rys. 4. Przykładowy wielomian w formie wewnętrznej

Implementacja CRC

Jedną z metod przyspieszających obliczenie sumy kontrolnej CRC jest wykorzystanie tablic odniesienia (ang. lookup tables). Wymaga to alokacji pewnej przestrzeni pamięci, która zwiększa się wykładniczo wraz ze wzrastającą wydajnością.

Przygotowując oprogramowanie dla procesora Blackfi ne, można wykorzystać dedykowane instrukcje znajdujące się na podstawowej liście rozkazów: BXOR oraz BXORSHIFT. Są one zoptymalizowane do operacji na rejestrach LFSR, przez co oferują większą wydajność obliczeń bez konieczności stosowania tablic odniesienia. Wyznaczenie CRC wymaga dwóch cykli maszynowych na każdy bit wejściowy. Instrukcje te są szczególnie przydatne, gdy dostępna pamięć jest mocno ograniczona.

Przykładowy program z ich wykorzystaniem został przedstawiony na rysunku 5. Składa się z trzech części. W pierwszej części znajduje się kod inicjalizacji. Inicjalizowany jest rejestr stanu LFSR (A0) oraz maska zawierająca współczynniki wielomianu generatora (A1).

Odnosząc się do rysunku 2 przedstawiającego rejestr w postaci zewnętrznej, jest on wypełniany od strony najmniej znaczącego bitu LSB przez współczynnik wyższego rzędu wielomianu generatora. W niniejszym programie przykładowym 32-bitowa wiadomość mieści się w jednym rejestrze i jest wprowadzona do LFSR, począwszy od najbardziej znaczącego bitu.

Drugą część programu stanowi pętla wykonywana k razy. W każdej iteracji pobierany jest bit z wiadomości, umieszczany w rejestrze CC procesora i wprowadzany do rejestru LFSR. Zawartość rejestru jest uaktualniana przez rozkaz BXORSHIFT. Kolejnym krokiem jest maskowanie A1 przez A0, poddawanie wyniku działaniu operacji XOR i dodawanie do bitu wejściowego (rejestr CC). Bit wynikowy jest wprowadzany na najmniej znaczącą pozycję A0. Zawartość rejestru ulega przesunięciu w lewo. Wiadomości dłuższe niż 32-bitowe wymagają zwiększenia liczby przejść pętli i sukcesywnego zastępowania zawartości rejestru R2.

W trzeciej, ostatniej części programu wykorzystany jest drugi wariant instrukcji BXORSHIFT – pozbawiony sprzężenia zwrotnego. W tym wariancie operacja przesunięcia jest wykonywana przed operacją XOR. Konieczne jest uprzednie wyliczenie pierwszego bitu na wyjściu przy użyciu instrukcji BXOR. Operuje ona na ostatniej wartości rejestru. Po tej operacji wykonywana jest pętla złożona z n-1 iteracji. W każdej z nich A0 jest uaktualniane i nowy bit wyjściowy jest umieszczany w rejestrze CC. Następnie rejestr R0 zawierający sumę CRC jest przesuwany w lewo, a na jego najmniej znaczącej pozycji umieszczany jest bit pochodzący z rejestru CC. Po zakończeniu tych operacji rejestr R0 zawiera obliczoną sumę kontrolną CRC.

Podsumowanie

Suma kontrolna CRC jest powszechnie spotykana w strumieniach danych cyfrowych. Efektywność jej wyznaczania decyduje w dużej mierze o szybkości pracy całego systemu, opóźnieniu w kodowaniu i dekodowaniu wiadomości oraz mocy obliczeniowej, jaka pozostaje do wykorzystania na inne cele. Stanowi ona nierozłączny element wymiany informacji i rezygnacja z niej jest często niemożliwa, dlatego efektywność algorytmu jest sprawą o istotnym znaczeniu.

Jakub Borzdyński