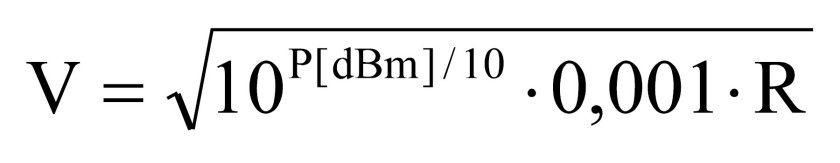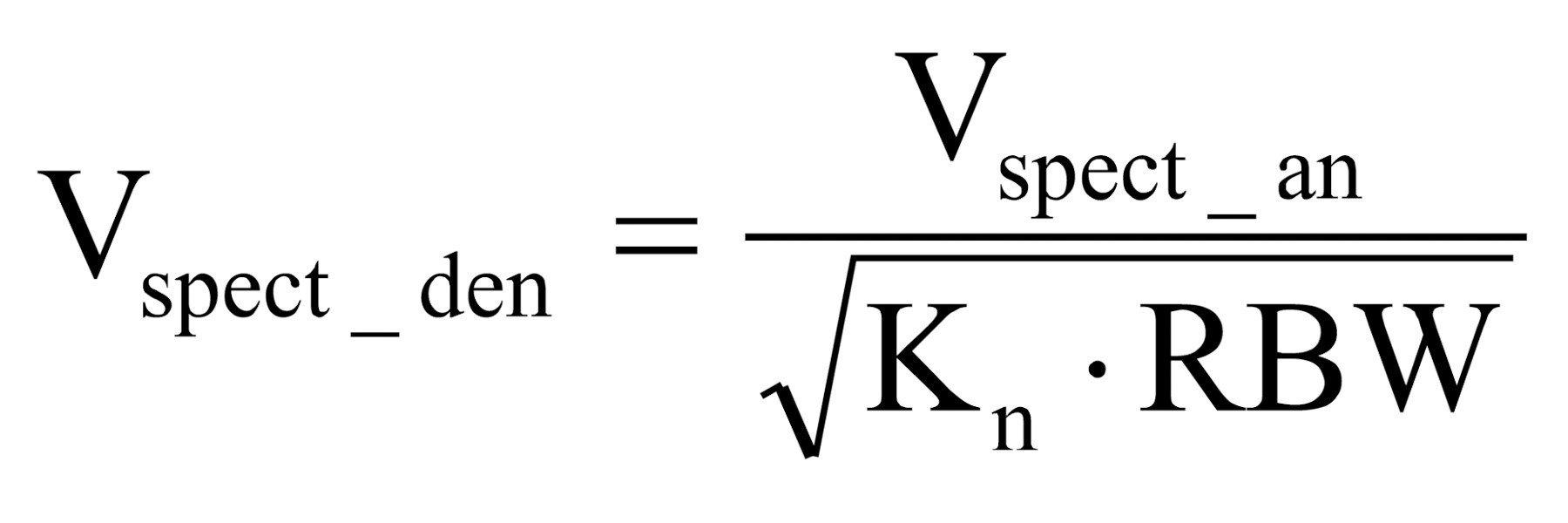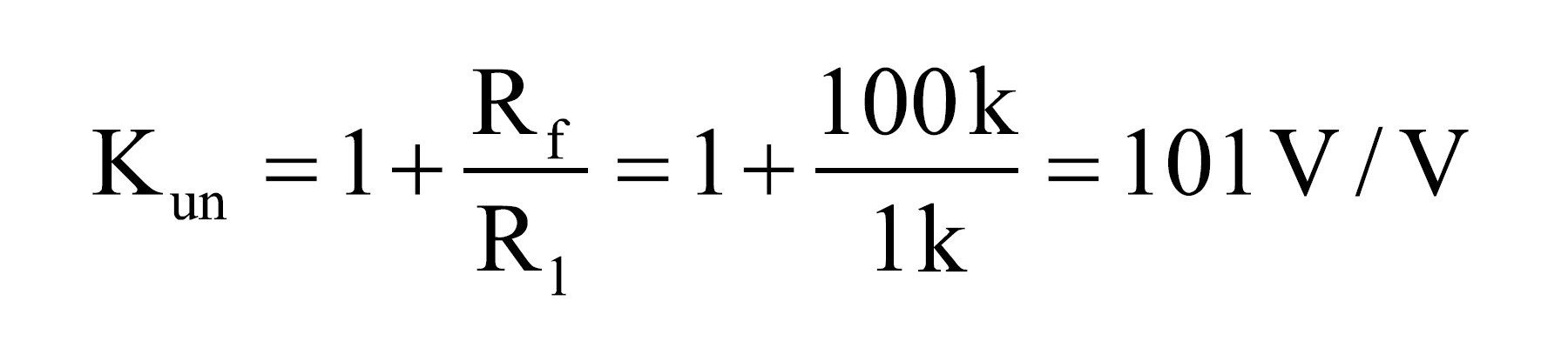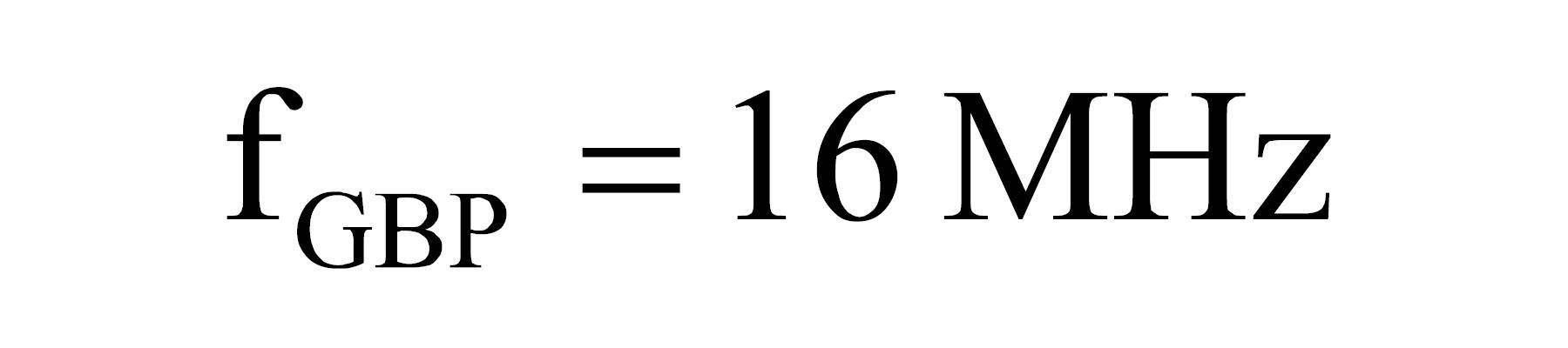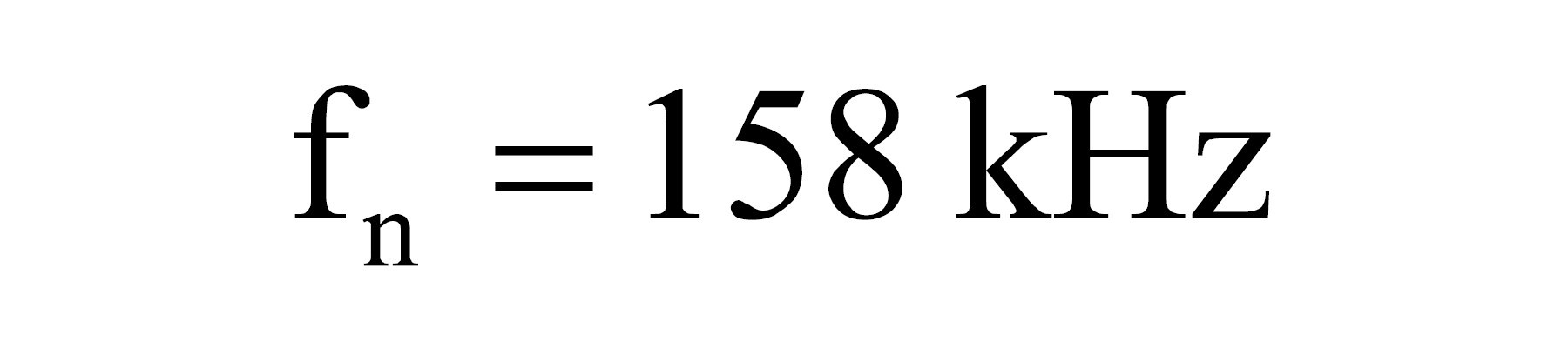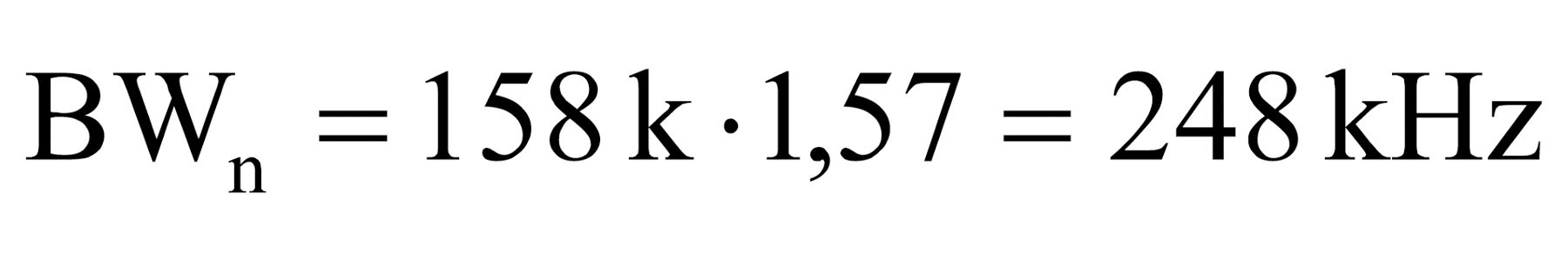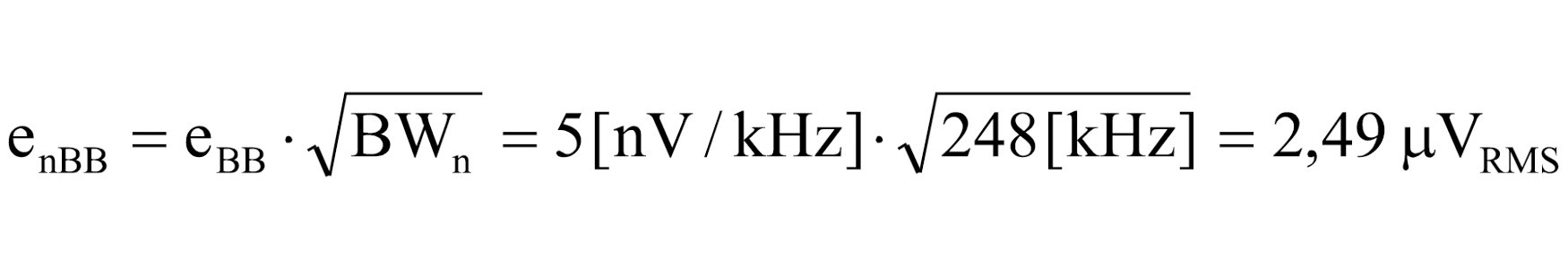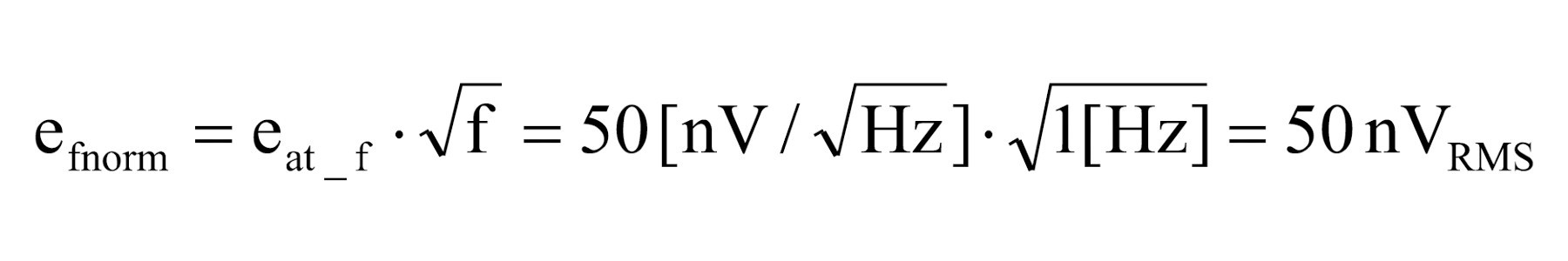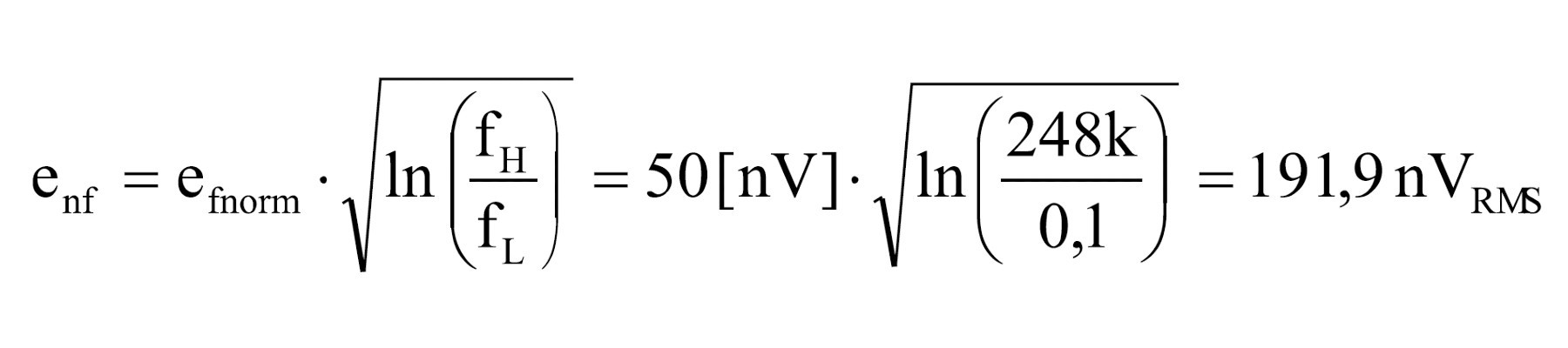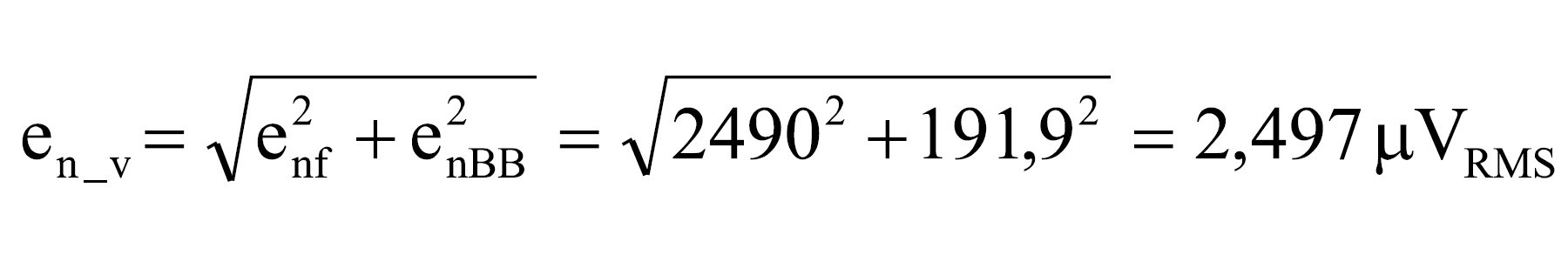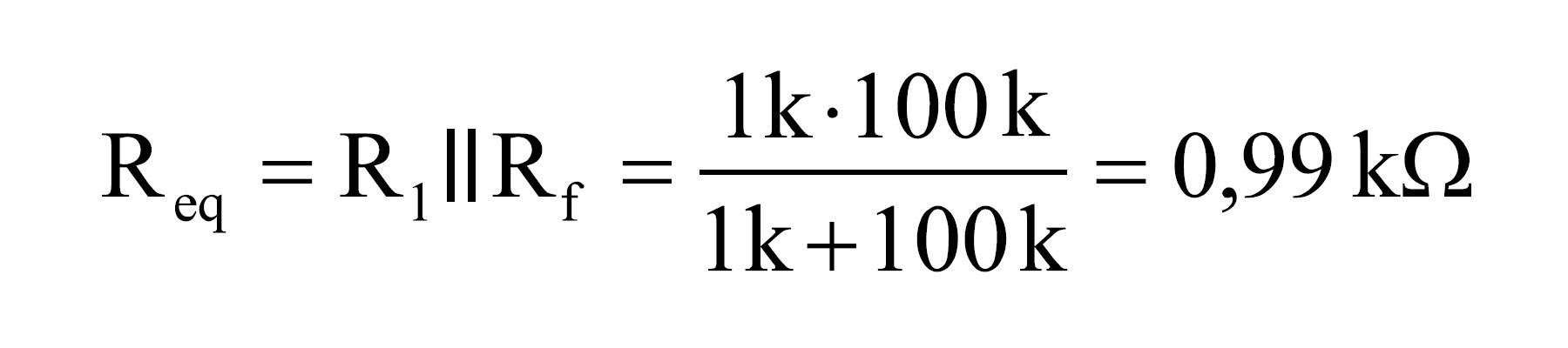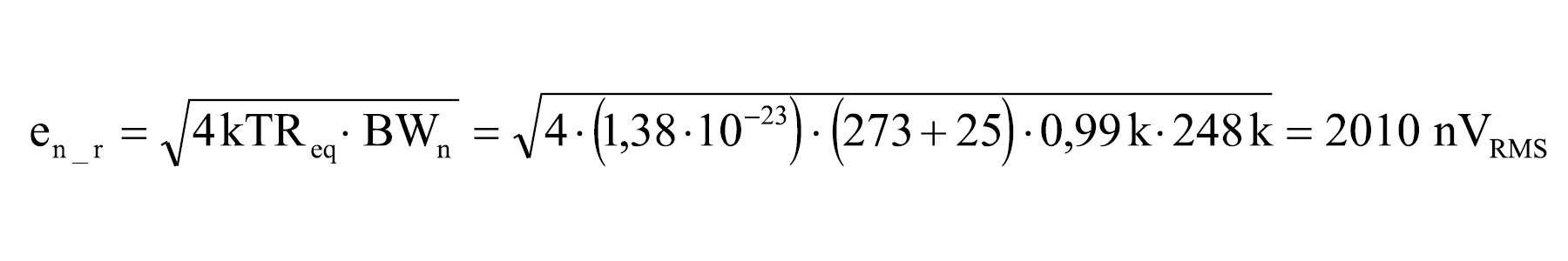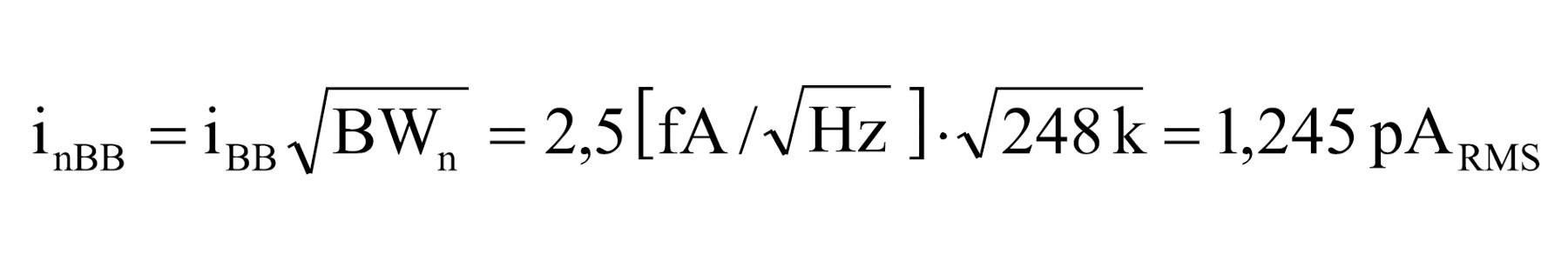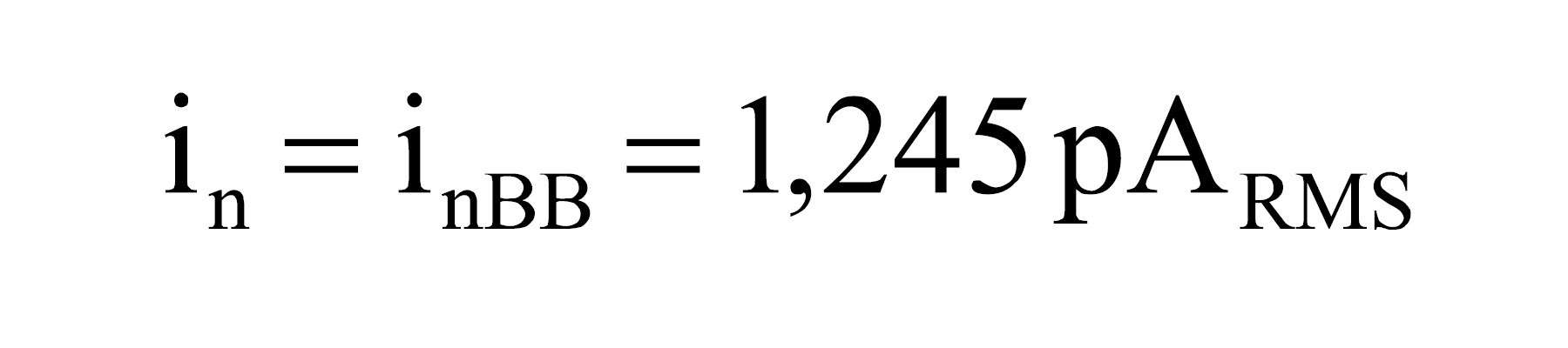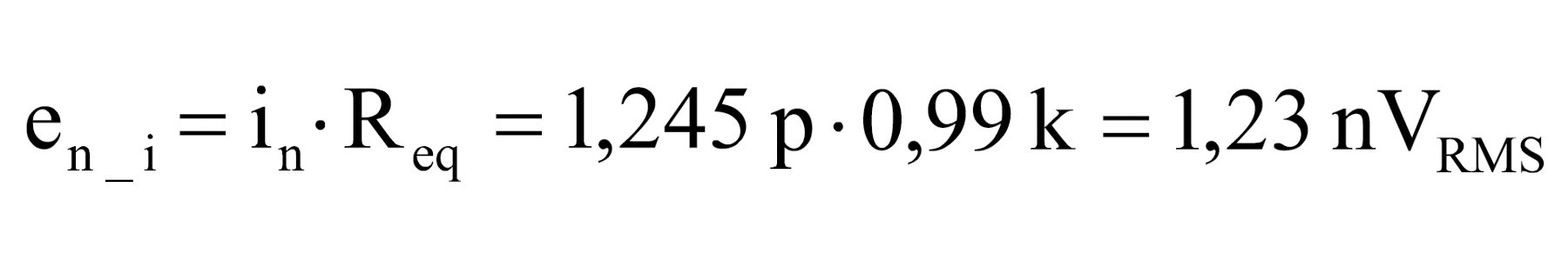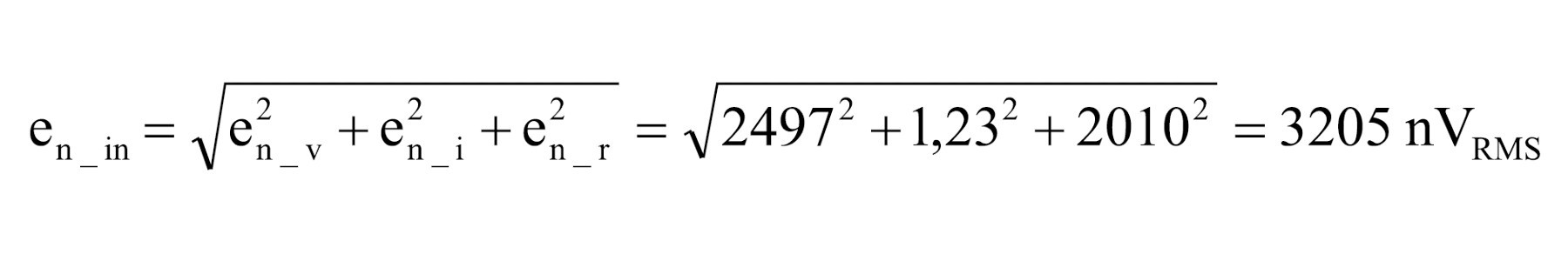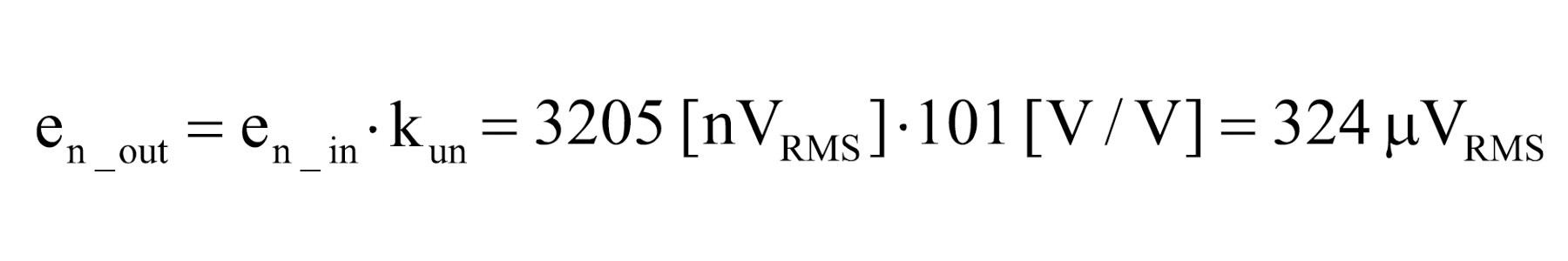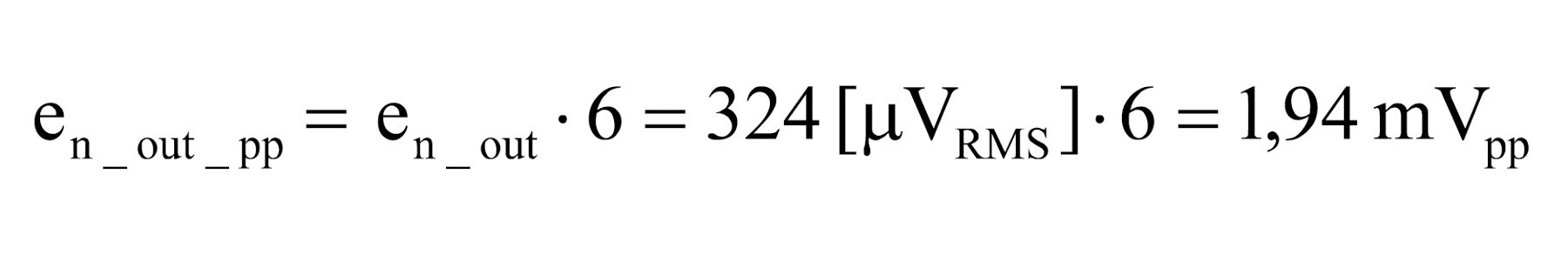Rodzaje szumów
W większości przypadków szumy są zjawiskiem szkodliwym. Zwykle obniżają jakość sygnału audio, są odpowiedzialne za powstawanie błędów w precyzyjnej technice pomiarowej. Trzeba jednak pamiętać o technice tzw. ditheringu stosowanej czasami np. w urządzeniach audio wykorzystujących przetworniki analogowo-cyfrowe i cyfrowo- analogowe do... polepszania jakości sygnału. W urządzeniach takich szum jest celowo dodawany do sygnału, co w efekcie korzystnie wpływa na subiektywną ocenę jakości dźwięku. To jednak temat na odrębny artykuł.
Szumy można ogólnie podzielić na zewnętrzne i wewnętrzne. Szumy zewnętrzne są generowane przez źródła znajdujące się poza układem elektronicznym. Często ich źródłem są układy zasilające, przetwornice impulsowe, sieć zasilająca 50 Hz, układy cyfrowe itp. Szumy wewnętrzne powstają w wewnętrznych elementach układu elektronicznego. Są to szumy termiczne, szumy migotania (fl icker noise), szumy szerokopasmowe itd. W artykule opisano metody szacowania szumów wewnętrznych. W dalszej części zawarto praktyczne przykłady pomiarów szumu z użyciem trzech rodzajów przyrządów: miernika True RMS, oscyloskopu i analizatora widma.
Pomiar szumu przyrządami True RMS
Zdolność do pomiaru rzeczywistej wartości skutecznej (True RMS) jest niezbędna ze względu na charakter sygnału. Szum w niczym nie przypomina idealnego sygnału sinusoidalnego, jaki mierzą zwykłe mierniki, więc pomiar takim przyrządem byłby właściwie nieprzydatny. Przypomnijmy, że pomiar zwykłym miernikiem polega de facto na zmierzeniu wartości maksymalnej i pomnożeniu wyniku przez współczynnik 0,707. Współczynnik ten określa zależność pomiędzy napięciem maksymalnym a skutecznym dla czystej sinusoidy. Mierniki True RMS działają na zupełnie innej zasadzie, polegającej na próbkowaniu sygnału i obliczaniu prawdziwej wartości skutecznej na podstawie tak uzyskanego zbioru danych.
Kolejną kwestią jest rodzaj sprzężenia wejścia miernika z digitizerem. Stosowane są sprzężenia "AC+DC" oraz "AC". Sprzężenie "AC+DC" dołącza wejście bezpośrednio do digitizera, więc pomiar uwzględnia obie składowe: zmienną i stałą. W sprzężeniu "AC" składowa stała jest odcinana i z tego względu jest to tryb preferowany do pomiarów szumów szerokopasmowych.
Zapewnienie omówionych wymagań jest dość proste. Duża część współcześnie produkowanych mierników spełnia odpowiednie warunki. Tu jednak kończą się dobre wiadomości. Kolejne wymagania są znacznie ostrzejsze. I tak: wymagane pasmo pomiarowe powinno rozciągać się od 20 Hz do 10 MHz, dokładność w całym paśmie powinna być nie gorsza niż 0,1%, wymagana własna podłoga szumu jest określana na maksymalnie 20 μV RMS dla zakresu 10 mV. Popularne przyrządy nie spełniają z reguły tych wymagań.
Pomiar szumu oscyloskopami
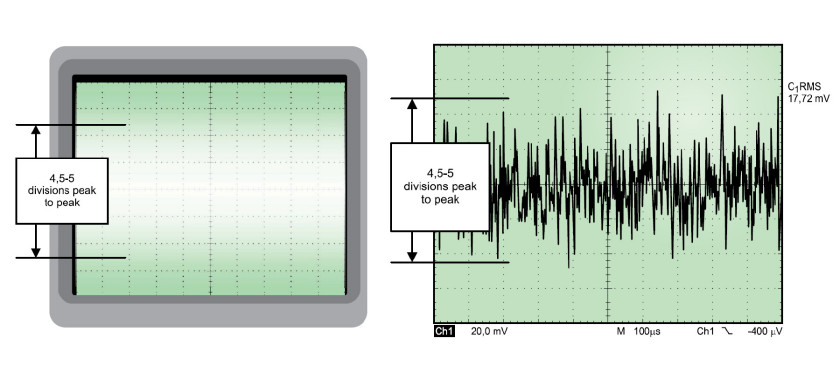
Wadą mierników True RMS jest to, że nie pokazują charakteru szumu. Tu z pomocą przychodzą oscyloskopy, które umożliwiają przyjrzenie się w dziedzinie czasu. A szum ten będzie wyglądał różnie, w zależności od jego charakteru. Można jeszcze zadać sobie pytanie, czy do pomiarów równie dobrze nadają się oscyloskopy cyfrowe, jak i analogowe. Pytanie takie jest jednak nieco retoryczne, gdyż coraz częściej nie mamy wyboru, oscyloskopy cyfrowe już niemal w pełni zdominowały rynek. Zobaczmy, jak wygląda szum oglądany oscyloskopem analogowym (fot. 1a) i cyfrowym (fot. 1b). Różnica jest dość znaczna i często narzekają na nią użytkownicy oscyloskopów cyfrowych. Z tego względu powstała m.in. np. rodzina oscyloskopów wyższej klasy, tzw. Digital Phosphor, które wyświetlają oscylogramy bardziej przypominające te, które obserwujemy na ekranach oscyloskopów analogowych. O kształcie szumu wyświetlanego na oscyloskopie analogowym decyduje: po pierwsze – losowy charakter, daleko odbiegający od przebiegu okresowego, w zasadzie uniemożliwiający zastosowanie skutecznego wyzwalania; po drugie – długi czas poświaty luminoforu powodujący jakby rozmycie przebiegu. W odróżnieniu od oscyloskopu analogowego, na oscyloskopie cyfrowym obserwujemy przebieg ostry i wyraźny. Trzeba jednak zauważyć, że oscyloskopy analogowe nie są przystosowane do pomiarów szumu 1/f. Zaletą przyrządów cyfrowych jest natomiast wyposażanie ich w funkcje ułatwiające pomiary, w tym szumu 1/f. Uzyskiwana w nich cyfrowa postać mierzonego przebiegu umożliwia wykonanie różnych obliczeń matematycznych, m.in. określenie wartości skutecznej napięcia szumu.
Ważną kwestią związaną z oscyloskopowymi pomiarami jest określenie własnej podłogi szumu. W tym celu konieczne jest zwarcie wejścia oscyloskopu. Można to zrealizować przez założenie odpowiedniej zworki na gnieździe BNC lub zwarcie końcówek sondy pomiarowej (jeśli jest to sonda ×1). Pamiętajmy, że używając sondy ×10, otrzymujemy 10 razy mniejszy sygnał niż w przypadku sondy ×1. Ponadto kabelek służący do dołączania masy w typowej sondzie może stanowić swego rodzaju antenę zbierającą wszelkie zakłócenia RFI/EMI. O wiele korzystniejsze jest stosowanie specjalnej krótkiej sprężynki łączącej masę, zakładanej na górny koniec sondy po zdjęciu kapturka normalnie chroniącego jej końcówkę (fot. 2).
Oscyloskopy cyfrowe mają zwykle filtr ograniczający pasmo (np. do 20 MHz). Oczywiste jest, że pasmo pomiarowe przyrządu powinno być szersze niż szerokość pasma mierzonego. Z drugiej strony jednak warto je ograniczać do pewnej częstotliwości powyżej zakresu mierzonego. Sensowne zatem będzie użycie takiego ogranicznika, gdy mierzony jest na przykład szum o szerokości pasma 100 kHz. Dzięki temu podłoga szumu będzie znacznie obniżona, gdyż zostaną wyeliminowane zakłócenia RFI/EMI.
Używając oscyloskopu do pomiaru szumów, należy również zwracać uwagę na typ sprzężenia. Nadal obowiązuje zasada, że dla szumów szerokopasmowych najbardziej odpowiednie jest sprzężenie AC. Na przykład mierząc szum źródła napięcia stałego 2 V przy zastosowaniu sprzężenia DC, stracimy wielokrotnie na czułości. Amplituda szumu jest przecież dużo mniejsza niż 2 V. Zdecydowanie inaczej będzie w pomiarze 1/f, którego widmo zaczyna się od zera i jest zawarte poniżej pasma pomiarowego oscyloskopu ze sprzężeniem DC. W takim pomiarze musi być zastosowane sprzężenie DC, bez obaw można też włączyć ogranicznik widma. Ogólne zasady, których warto przestrzegać w oscyloskopowych pomiarach, to: nieużywanie sond ×10, używanie krótkich połączeń GND montowanych na końcu sondy pomiarowej, rozważne korzystanie z ogranicznika pasma, rozważne stosowanie typu sprzężenia (zależne od charakteru mierzonego szumu).
Pomiar analizatorami widma
Jeśli zastanowić się nad wyborem najbardziej odpowiedniego przyrządu do pomiaru szumów, to analizator widma wydaje się najlepszą opcją. Szum jest wielkością fizyczną, której nie można rozpatrywać w oderwaniu od szerokości widma, w której jest mierzony. Z tego względu często nie mówi się o szumie, lecz rozważa się gęstość szumu. Jest to parametr o dość specyficznym i wzbudzającym wiele niezrozumienia wymiarze, jakim jest nV/√Hz. Analizatory widma wyświetlają wykresy mocy lub napięcia zbliżone do krzywych gęstości widmowej. Można w nich ponadto wybierać odpowiednie dla konkretnych potrzeb tryby pomiarowe, np. takie, które wyświetlają wyniki bezpośrednio w jednostkach gęstości widmowej. W innych przypadkach wynik musi być przemnażany przez współczynnik korygujący.
Podobnie jak oscyloskopy, tak i analizatory widma są produkowane już niemal w większości jako przyrządy cyfrowe. Wiele analizatorów analogowych przetrwało jednak do dziś w dobrym stanie i nadal są używane w pomiarach. Najczęściej spotykane są odmiany analizatorów superheterodynowych, w których sygnał wejściowy jest mieszany z sygnałem pochodzącym z lokalnego oscylatora przestrajanego. Zakres przestrajania odpowiada mierzonemu pasmu. W analizatorach cyfrowych widmo jest obliczane z wykorzystaniem szybkiej transformaty Fouriera (FFT), często z łączoną techniką superheterodynową.
Technika pomiaru widma analizatorem różni się nieco od pomiarów oscyloskopowych. Trzeba jednak zaznaczyć, że producenci oscyloskopów coraz częściej implementują obsługę funkcji FFT w sposób zbliżony, często wręcz identyczny z rozwiązaniami stosowanymi w analizatorach widma. Parametrami określającymi przebieg pomiaru są np.: częstotliwość początkowa i końcowa lub zakres tych częstotliwości (span) oraz częstotliwość filtru RBW określającego rozdzielczość. Najczęściej stosowaną w analizatorach jednostką pomiaru widma jest dBm, czyli moc mierzona w skali logarytmicznej, odnoszona do 1 mW. Jeśli mówimy o mocy, to należy podać, na jakiej rezystancji się ona wydziela. Najczęściej mamy do czynienia z wejściami 50 Ω lub 1 MΩ i to jest właśnie ta rezystancja. Przeliczenie tak uzyskanego wyniku na jednostkę napięcia RMS nie jest proste. Należy w tym celu skorzystać z zależności:
gdzie R – impedancja wejściowa analizatora (najczęściej 50 Ω lub 1 MΩ), P[dBm] – moc zmierzona w jednostkach dBm odnoszona do 1 mW.
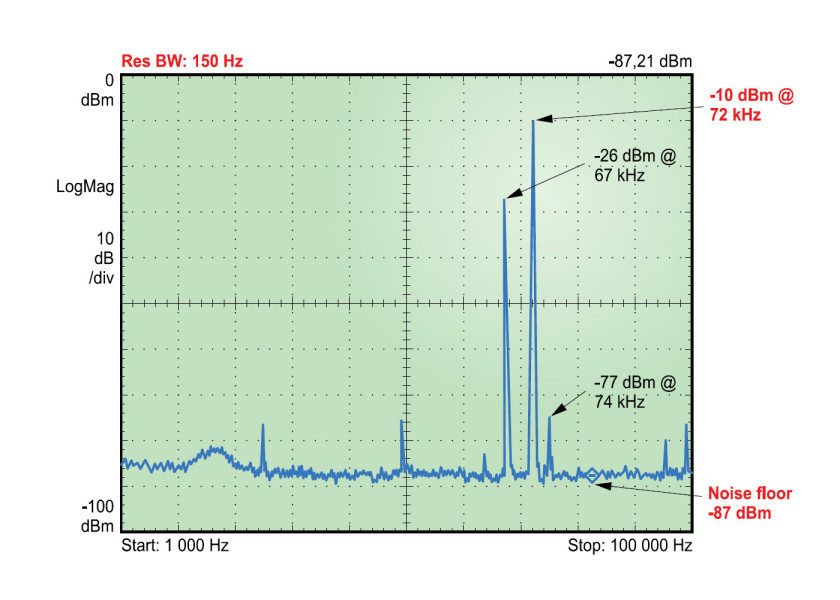
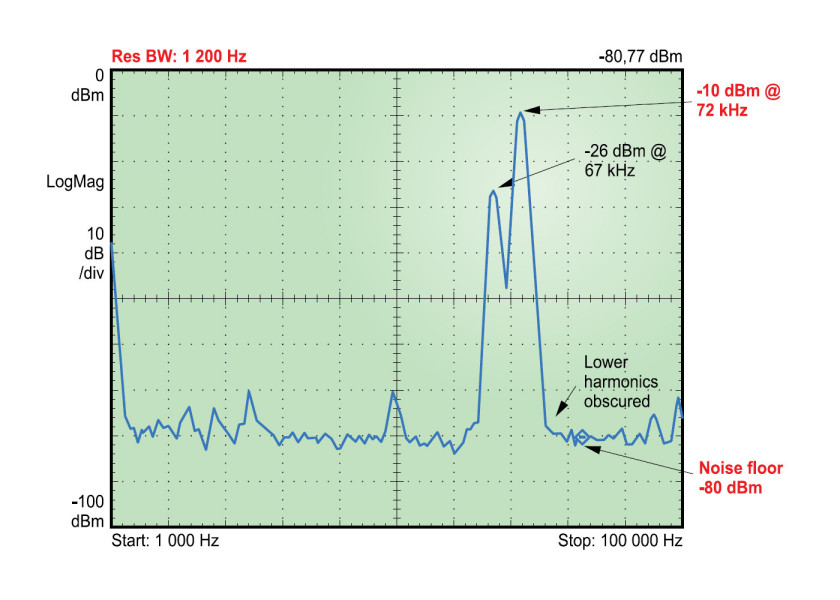
Na rysunku 3 przedstawiono wyniki pomiaru pewnego układu generującego wyraźne dwie składowe widma. Zmierzony poziom mocy mocniejszej z nich jest równy –10 dBm, co przy założeniu, że pomiaru dokonano na obciążeniu 50 Ω, odpowiada napięciu RMS równemu 0,0707 V. Warto zwrócić uwagę na to, że filtr RBW decydujący o rozdzielczości ustawiono na 150 Hz, a podłoga szumu ma w tym przypadku poziom –87 dBm. Następnie pomiar powtórzono (rys. 4), zmniejszając rozdzielczość (zwiększając szerokość filtru RBW do 200 Hz). Następstwem tego było podwyższenie podłogi szumu do poziomu –80 dBm przy jednoczesnym zachowaniu poziomu samego sygnału. Nadal miał on wartość –10 dBm. Podwyższenie podłogi wynika z tego, że mamy tu do czynienia z szumem termicznym. Zwiększenie szerokości pasma musiało więc skutkować jego zwiększeniem. Zmniejszenie rozdzielczości nie mogło natomiast zmienić zmierzonego poziomu sygnału sinusoidalnego mającego zawsze tę samą wartość niezależnie od szerokości pasma pasmowoprzepustowego filtru RBW. Na podstawie tej operacji można wyciągnąć wniosek, że sygnały dyskretne nie powinny być uwzględniane w obliczeniach gęstości widmowej mocy szumu. Przykładem jest chociażby szum wytwarzany przez sieć zasilającą 50 Hz.
Jeśli analizator nie ma opcji wyświetlania widma w jednostkach gęstości mocy (nV/√Hz), należy takie obliczenie wykonać ręcznie, dzieląc wynik z analizatora przez pierwiastek kwadratowy z szerokości pasma RBW. Zauważmy, że do przekonwertowania szerokości pasma RBW do szerokości pasma szumu potrzebny jest odpowiedni współczynnik konwersji. Do przeliczenia zmierzonej mocy widmowej w jednostce dBm na widmową gęstość mocy należy skorzystać z zależności:
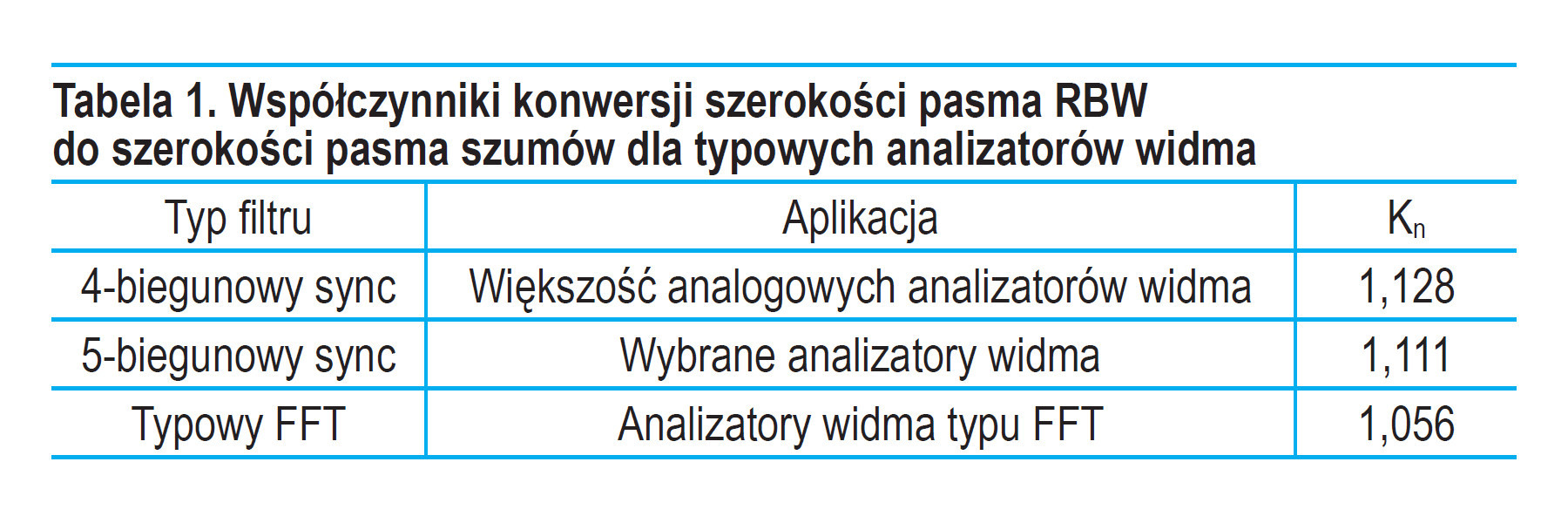
gdzie: Vspect_an – napięcie RMS obliczone z poprzedniej zależności, Kn – współczynnik konwersji, RBW – szerokość pasma filtru RBW ustawiona w analizatorze, Vspect_den – gęstość widmowa mocy (w nV/√Hz).
W tabeli 1 zamieszczono kilka przykładowych współczynników konwersji podawanych przez Agilenta (obecnie Keysight Technologies) – nota aplikacyjna 1303 (2003).
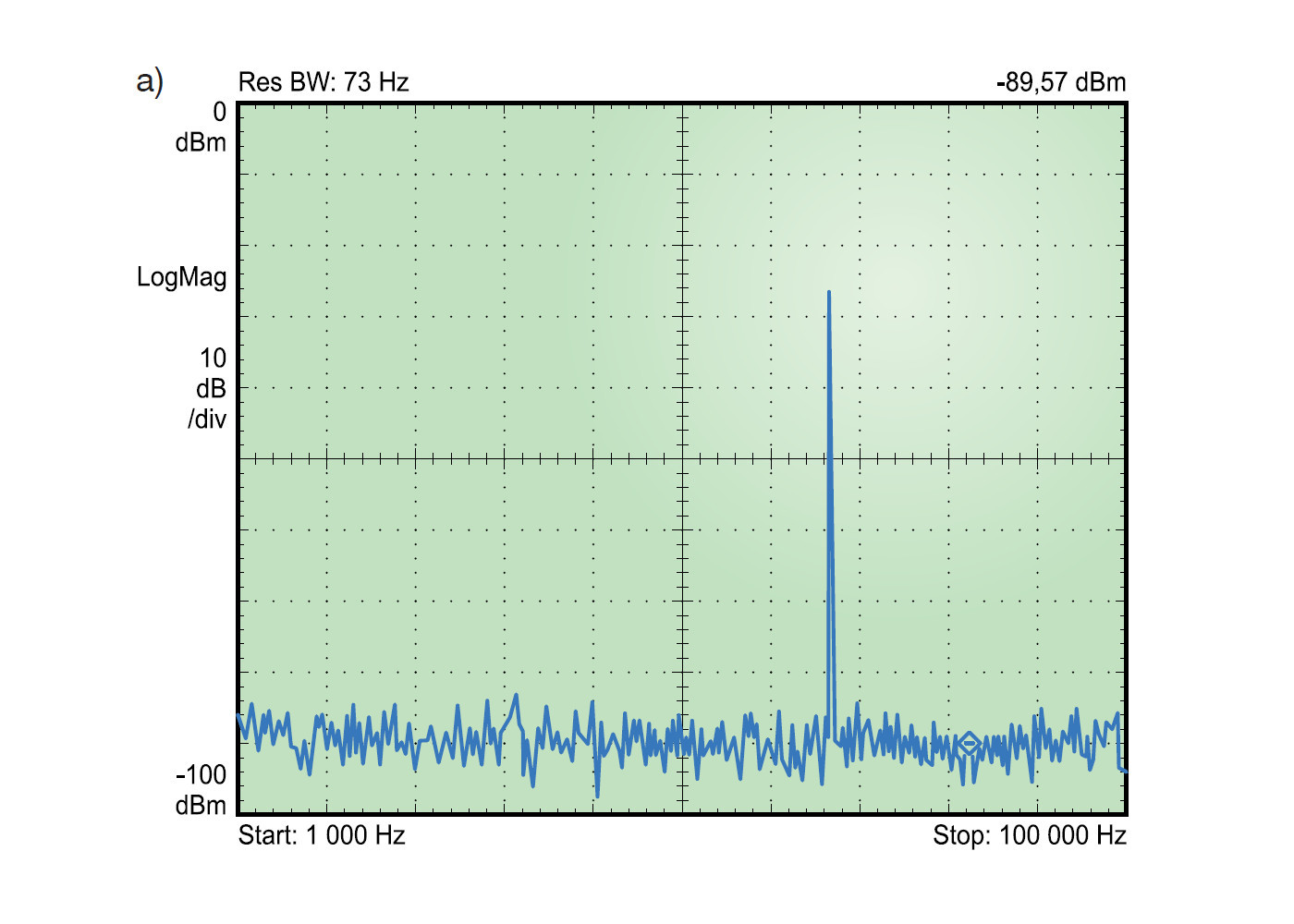
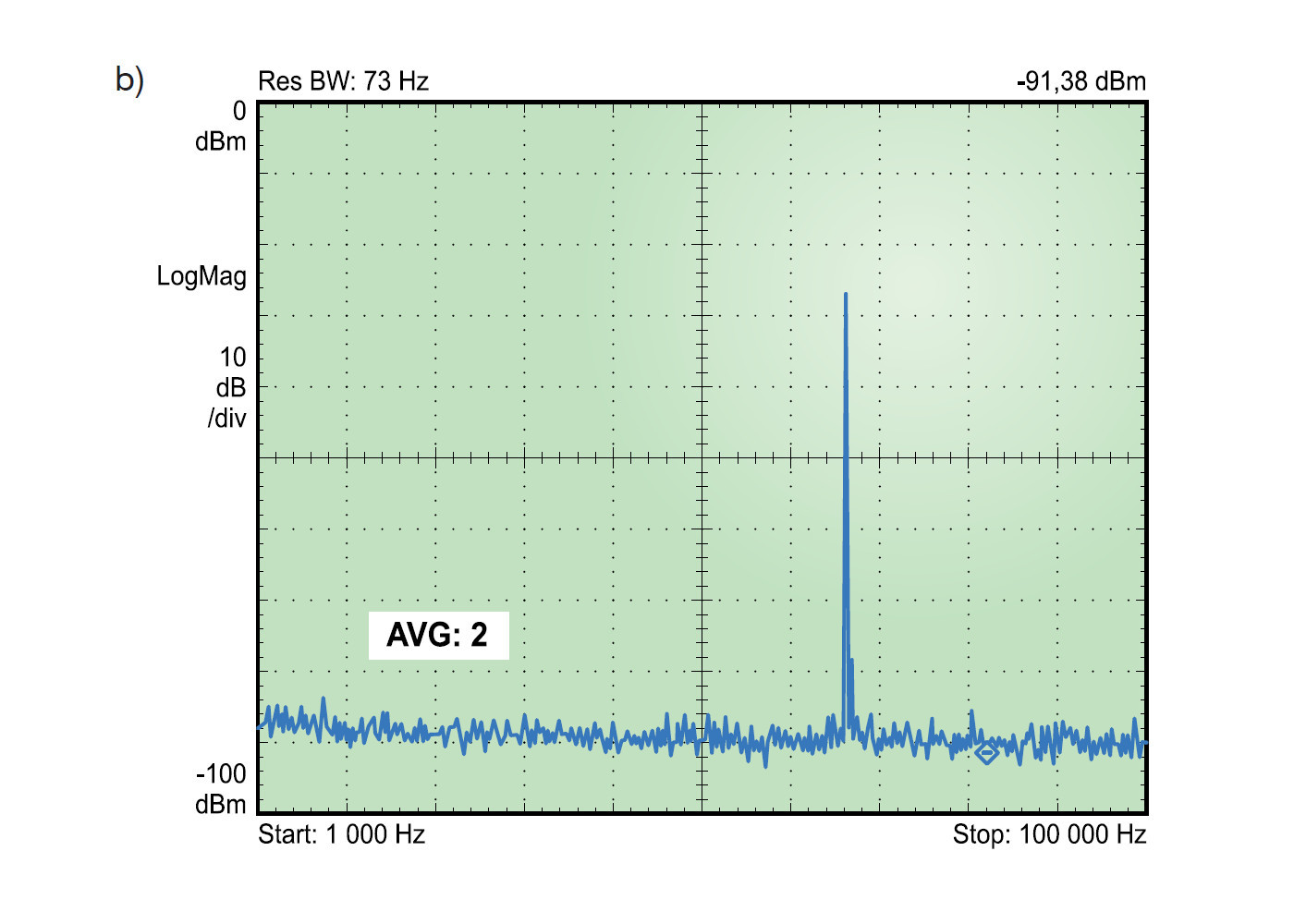
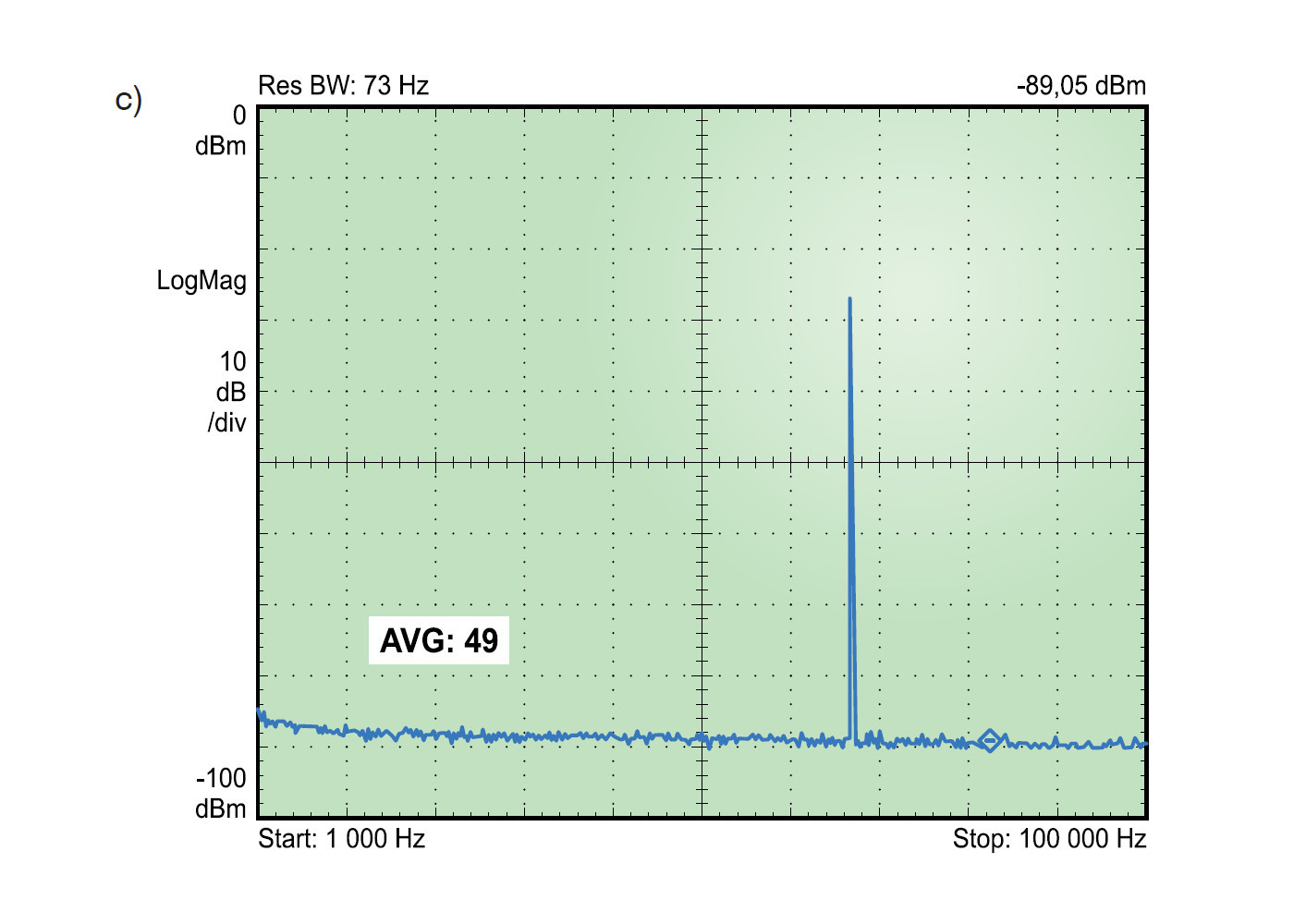
W pomiarach szumu analizatorami widma należy wziąć pod uwagę jeszcze jedną własność tych przyrządów, która może mieć wpływ na interpretację pomiarów. Większość analizatorów ma opcję uśredniania wyników. Jest ona realizowana programowo metodami cyfrowymi. Włączenie uśredniania zmniejsza różnice pomiędzy wykresami widma wyświetlanymi w kolejnych cyklach akwizycji. Liczba uśrednień jest ustalana elementami regulacyjnymi analizatora i mieści się zwykle w przedziale od 1 do 100. Na rysunku 5a-c przedstawiono pomiar tego samego sygnału z różną liczbą uśrednień (rysunek 5a – bez uśredniania, rysunek 5b – liczba uśrednień równa 2 i rysunek 5c – liczba uśrednień równa 49).
Ekranowanie
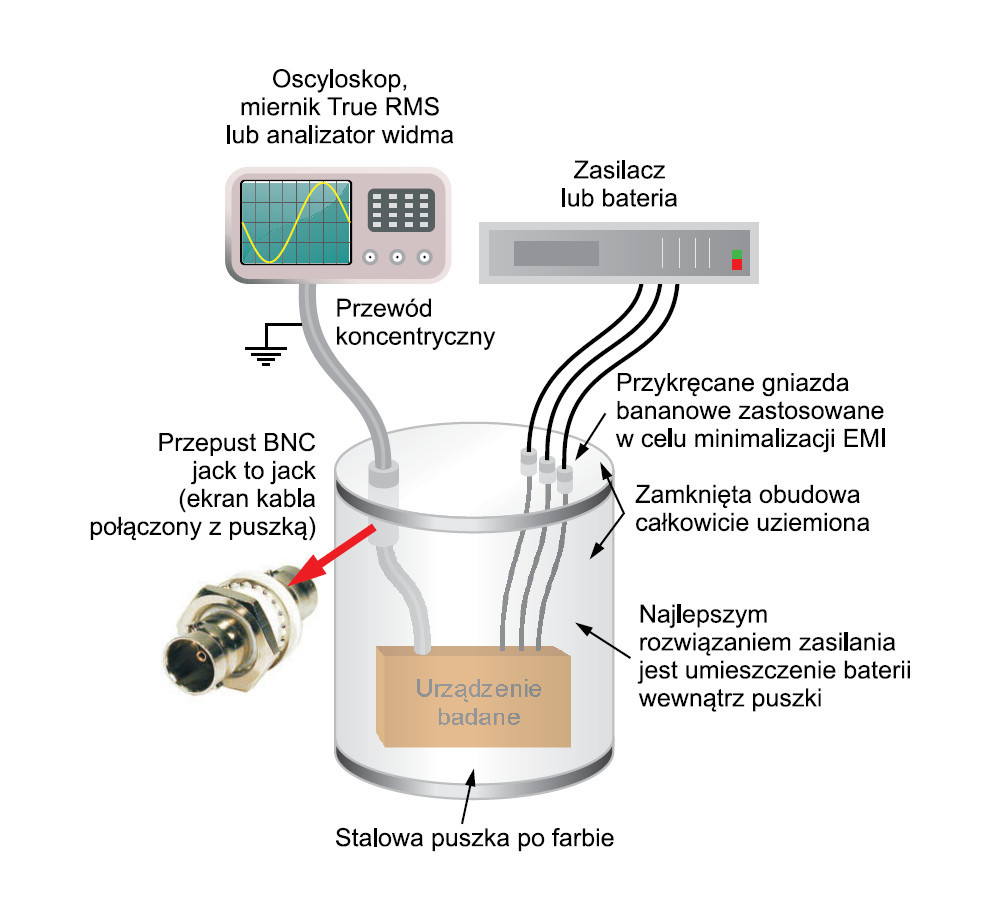
Mierząc szumy wewnętrzne, należy oczywiście zadbać o to, by nie nakładały się na nie szumy zewnętrzne. Zwykle stosuje się w tym celu ekranowanie, najlepiej w postaci osłoniętej z każdej strony obudowy. Najczęściej są one wykonywane z miedzi, żelaza lub aluminium. Tak wykonana obudowa powinna być połączona z masą układu. Pewnym problemem są wyprowadzenia sygnałów i kabli zasilających. Są one wyprowadzane przez małe otwory wykonane w obudowie. Niezwykle ważne jest, aby minimalizować zarówno średnice otworów, jak i ich liczbę, gdyż to one stanowią główne punkty przecieków. Oprócz otworów warto jeszcze zwrócić uwagę na szwy i łączenia elementów obudowy. Jeśli możliwe jest umieszczenie źródeł zasilających wewnątrz ekranującej obudowy, na pewno warto z tego skorzystać. Przykładową obudowę ekranującą wykonaną z puszki po farbie przedstawiono na fotografii 6, a na rysunku 7 zamieszczono schemat połączeń.
Zastosowanie puszki jest bardzo wygodne, gdyż zapewnia ona dokładne ekranowanie i względnie łatwy dostęp do badanego urządzenia (DUT). Ważne jest, aby sygnały we/wy były wyprowadzone przewodami koncentrycznymi z zastosowaniem przepustów BNC typu jack to jack. Należy również zadbać o dobre połączenie ekranu kabla z puszką, a także o dokładne zamknięcie puszki.
Określenie podłogi szumu
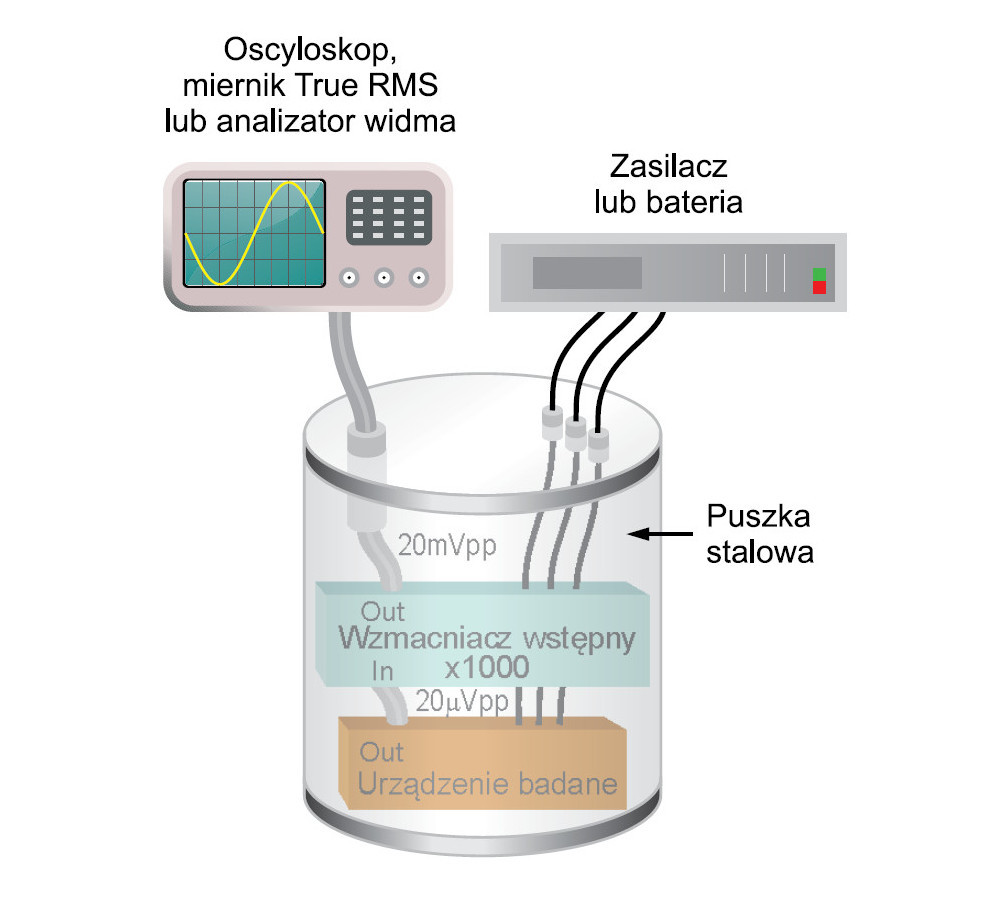
Celem prowadzonych badań jest pomiar szumu wyjściowego występującego w układach niskoszumowych lub wytwarzanego przez elementy. Jest to dość trudne zadanie, gdyż poziom mierzonego szumu jest często poniżej możliwości dostępnego sprzętu. Zwykle konieczne jest więc stosowanie dodatkowego wzmacniacza niskoszumowego włączanego pomiędzy DUT a przyrząd pomiarowy (rys. 8). Kluczowym zagadnieniem jest zapewnienie, aby szum takiego wzmacniacza wstępnego był mniejszy niż szumy urządzenia badanego. W praktyce przyjmuje się, że szum wzmacniacza wstępnego powinien być trzykrotnie niższy od szumu DUT. Procentowy błąd względny pomiaru podłogi szumu jest wówczas równy ok. 6%. Wstępne sprawdzenie podłogi szumu jest niezwykle ważnym krokiem, który powinien być wykonany przed przystąpieniem do pomiarów. Pomiar podłogi szumu polega zazwyczaj na zwarciu wejścia bloku wzmacniającego lub przyrządu pomiarowego. Pominięcie tego kroku skutkuje błędnymi wynikami pomiarów szumu.
Przykład 1 – pomiar szumu z użyciem miernika True RMS
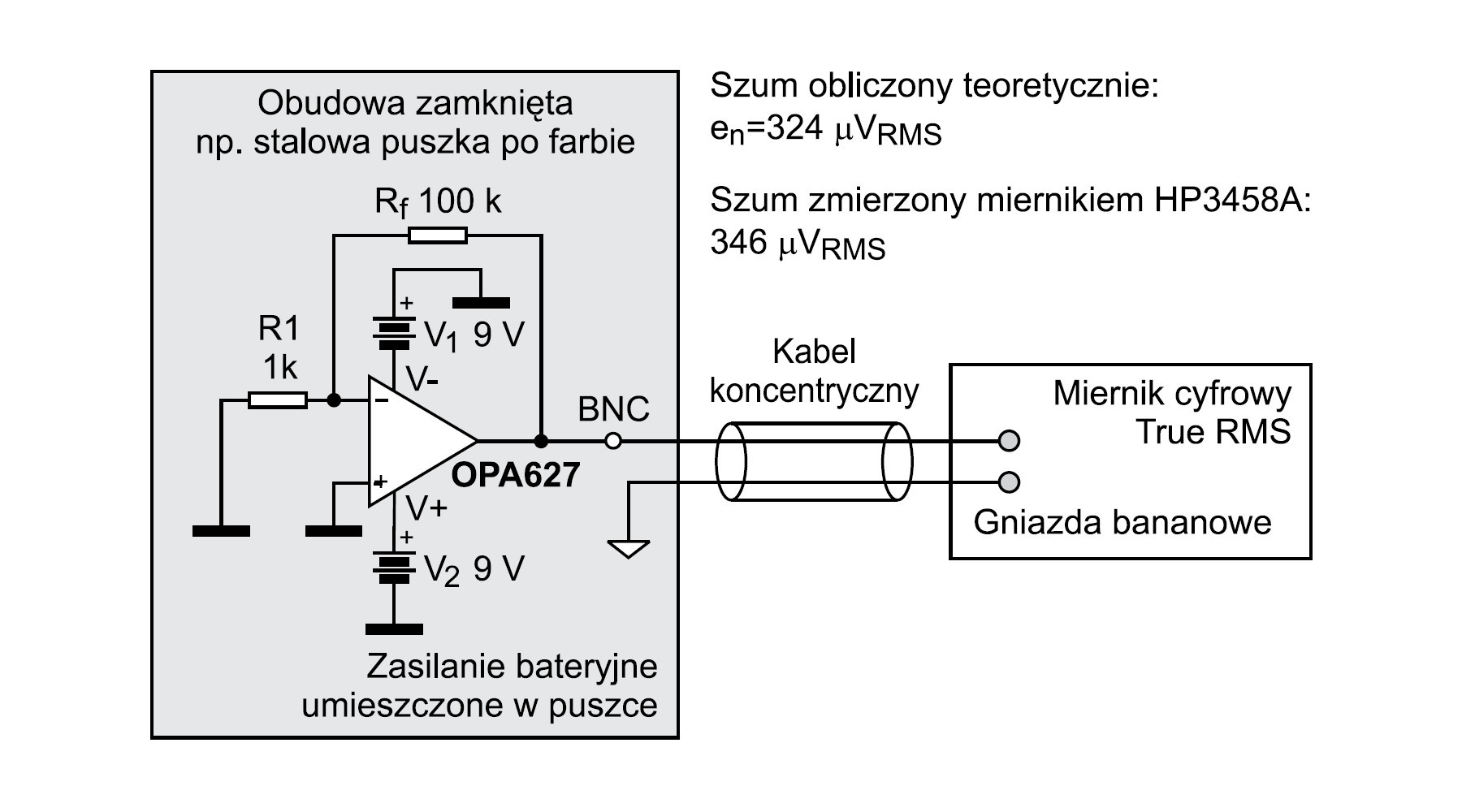
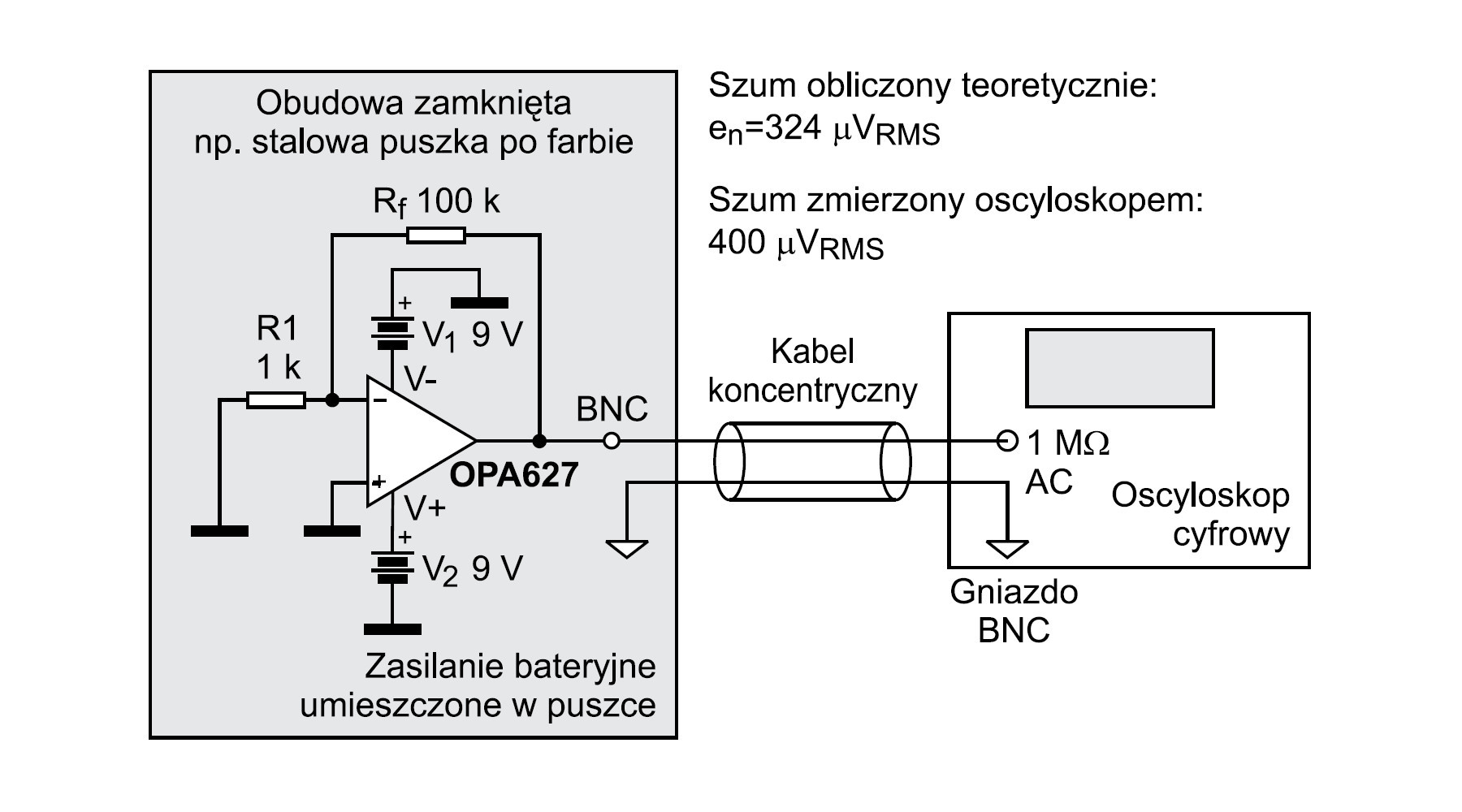
Od teorii powoli przechodzimy do praktyki. Na warsztat bierzemy wzmacniacz operacyjny OPA627 pracujący w konfiguracji z wejściem nieodwracającym. Schemat układu pomiarowego przedstawiono na rysunku 9. Pomiaru szumu na wyjściu wzmacniacza OPA627 nie dokonujemy jednak tylko z czystej ciekawości. Wcześniej szumy te były dokładnie obliczone na podstawie danych katalogowych i teraz tylko je weryfikujemy. W zasadzie obliczenia wymagałyby odrębnego artykułu, więc tutaj podajemy je tylko w telegraficznym skrócie (patrz ramka "Kluczowe cechy techniczne"). Z zamieszczonych obliczeń wynika, że na wyjściu rozpatrywanego wzmacniacza należy spodziewać się szumu o napięciu skutecznym 324 μV. Pomiar wykonany miernikiem cyfrowym HP3458A dał wynik 346 μV. Mamy więc prawie 7-procentową różnicę w odniesieniu do wartości obliczonej. Biorąc pod uwagę złożoność rozpatrywanych zjawisk i wpływ wielu czynników, odchyłka ta wydaje się dość dobrym rezultatem.
Przykład 2 – pomiar szumu z użyciem oscyloskopu
Tym razem do pomiarów tego samego układu użyto oscyloskopu (rys. 10). Przyrządem tym łatwiej jest mierzyć napięcie międzyszczytowe szumu i na tej podstawie ewentualnie obliczać napięcie skuteczne. Okazało się, że napięcie międzyszczytowe jest równe 2,4 mV, co po podzieleniu przez 6 daje wynik 400 μVRMS. Współczynnik 6 wynika z rozważań statystycznych. Jak widać, pomiar oscyloskopem dał gorszy wynik. Tym razem różni się w stosunku do wartości obliczonej o 23%. To sporo, ale nie będziemy tu rozważać przyczyn takiego stanu.
Przykład 2 – pomiar szumu z użyciem analizatora widma
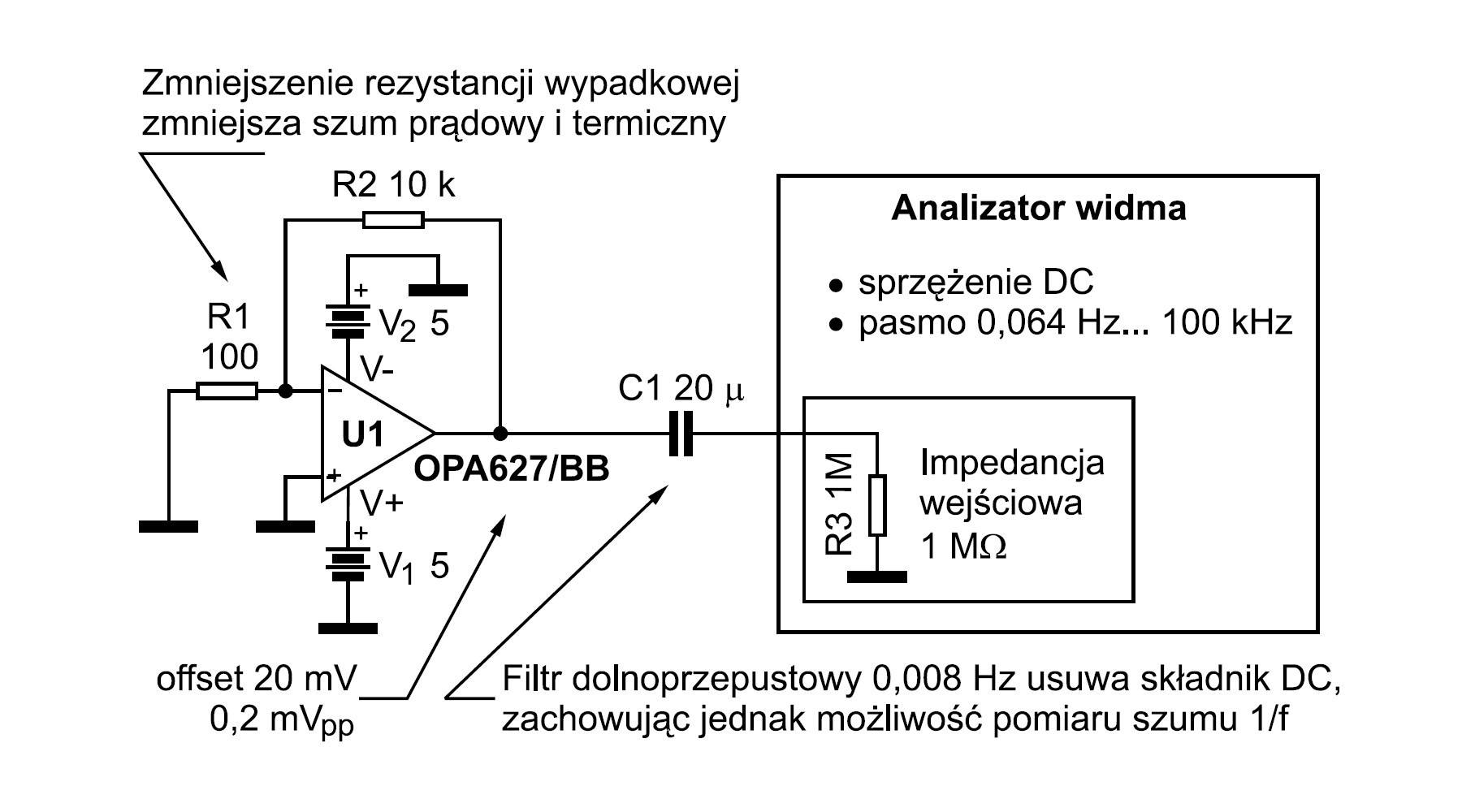
Pozostaje jeszcze pomiar analizatorem widma. Schemat stanowiska pomiarowego przedstawiono na rysunku 11. Zakres pomiarowy analizatora rozciąga się od 0,064 Hz do 100 kHz, co pozwala mierzyć zarówno szum 1/f, jak i szum szerokopasmowy różnych wzmacniaczy. Analizator jest wewnętrznie skonfigurowany do pracy ze sprzężeniem stałoprądowym. Zrezygnowano ze sprzężenia AC w przyrządzie, gdyż dolna częstotliwość graniczna byłaby wówczas równa 1 Hz, co uniemożliwiałoby pomiar szumu 1/f. Z drugiej strony taki rodzaj sprzężenia jest pożądany ze względu na duży off set wyjściowy wzmacniacza OPA627 zastosowanego w DUT. Z tego względu zastosowano zewnętrzne sprzężenie AC z użyciem kondensatora C1 (20 μF). Częstotliwość graniczna jest w takim rozwiązaniu równa 0,008 Hz, a więc możliwy jest pomiar szumu 1/f. Trzeba zaznaczyć, że zalecane jest użycie kondensatorów ceramicznych (wielu kondensatorów o mniejszej pojemności połączonych równolegle) zamiast kondensatorów elektrolitycznych lub tantalowych.
Można również rozważyć kwestię rezystancji wypadkowej w obwodzie sprzężenia zwrotnego układu OPA627, która jest równa równoległemu połączeniu rezystorów R1 i R2. Rezystancja ta ma wpływ na szum prądowy i szum termiczny i powinna być minimalizowana. W tym przykładzie oporności są 10-krotnie mniejsze niż w poprzednich pomiarach. Przy wzmocnieniu 100 V/V charakterystyka przenoszenia wzmacniacza OPA627 załamuje się przy częstotliwości ok. 160 kHz, ale nie ma to znaczenia, gdyż górna częstotliwość pomiarowa analizatora jest równa 100 kHz.
Omówienie wyników pomiaru analizatorem widma będzie wyglądało nieco inaczej, niż miało to miejsce w przypadku pomiarów miernikiem True RMS i oscyloskopem. Wynika to z zasady działania przyrządu.
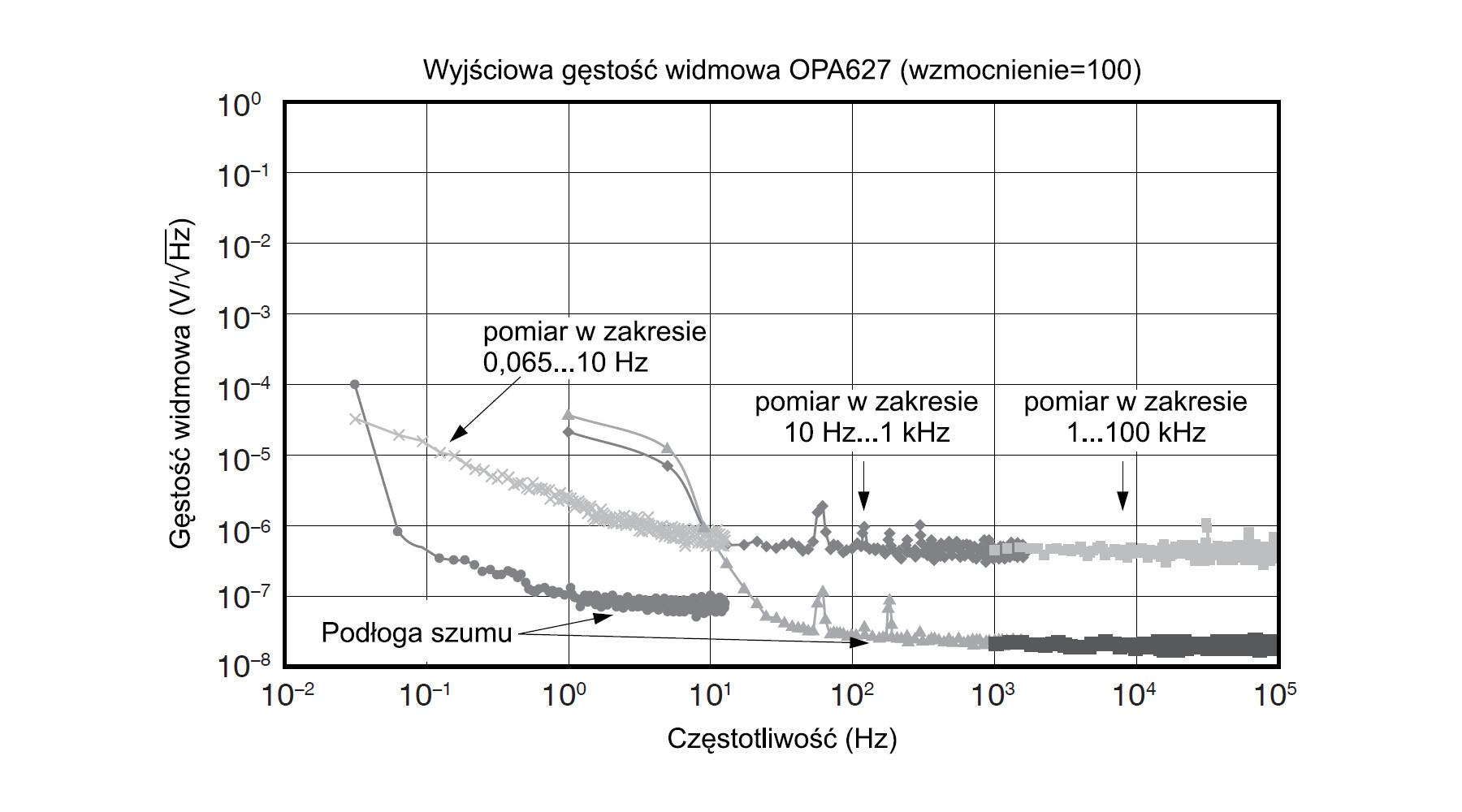
Pomiar przeprowadzono w trzech zakresach: 0,064...10 Hz, 10 Hz...1 kHz, 1 kHz...100 kHz (rys. 12). O zastosowaniu przedziałów zadecydowało liniowe przemiatanie częstotliwości w użytym analizatorze. Problem najlepiej wyjaśni przykład. Gdyby przyjąć rozdzielczość pomiarową np. 0,1 Hz, byłaby ona za mała dla najniższych częstotliwości analizowanych, a dla najwyższych byłaby wręcz nadmierna. Poza tym, jak łatwo obliczyć, do analizy całego przyjętego zakresu z rozdzielczością 0,1 Hz analizator musiałby zgromadzić 106 punktów. Dzieląc pasmo badane na kilka zakresów, można sensownie dobrać w każdym z nich optymalną rozdzielczość przy akceptowalnej liczbie punktów. W omawianym pomiarze przyjęto rozdzielczość 0,01 Hz dla pierwszego zakresu, dla ostatniego natomiast jest ona równa 100 Hz.
Na wykresie z rysunku 12 widoczne są typowe anomalie często występujące w pomiarach analizatorem widma. Wyraźnie można zlokalizować szpilkę pochodzącą od sieci zasilającej i jej harmoniczną. Takie zakłócenia są często generowane w układach samego analizatora i trudno ich uniknąć. Problemem jest też dość duży błąd występujący dla najmniejszych częstotliwości zakresu. Analizator mierzy pasmo z użyciem przestrajanego filtru pasmowoprzepustowego. Szerokość pasma tego filtru w odniesieniu do częstotliwości filtrowanej jest dużo gorsza dla małych częstotliwości niż dla dużych. Znowu posłużymy się przykładem. Załóżmy, że analizator mierzy pasmo od 1 Hz do 1 kHz, a przemiatanie częstotliwości odbywa się z użyciem filtru pasmowoprzepustowego o paśmie 1 Hz. Nietrudno zauważyć, że w stosunku do mierzonych częstotliwości filtr ten ma pasmo bardzo szerokie dla dolnych częstotliwości zakresu i wystarczająco wąskie dla górnych.
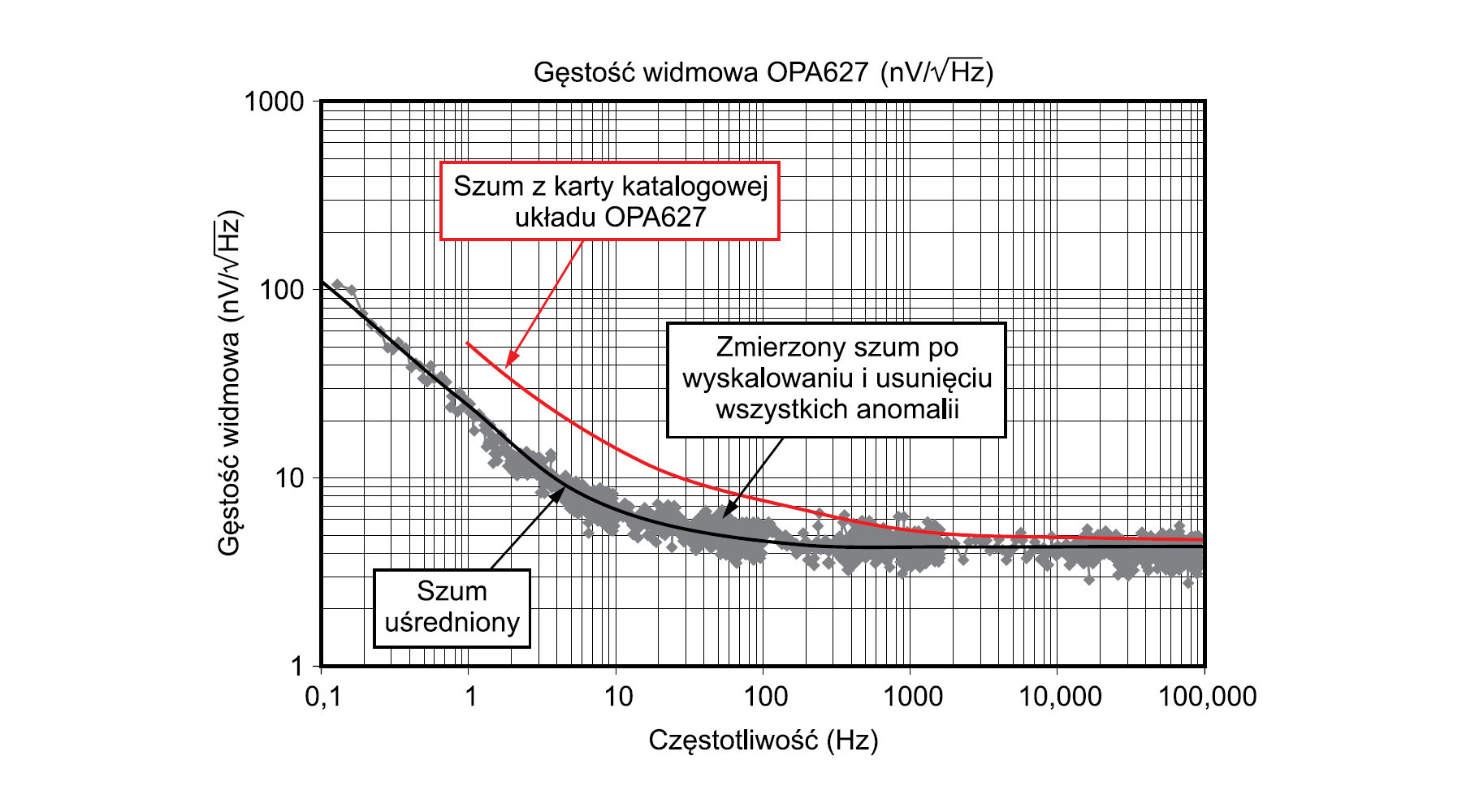
Wyników pomiaru szumu analizatorem nie można brać bezkrytycznie, należy im się przyjrzeć i wyeliminować rozpoznane błędy i niedokładności (omówione wyżej). Po wyczyszczeniu wszystkich anomalii i uśrednieniu pomiarów otrzymujemy widmo (napięciową gęstość widmową) przedstawione na rysunku 13. Należy jeszcze zwrócić uwagę na to, że w katalogach parametr ten jest odnoszony do wejścia, aby więc można było porównać rezultaty mozolnie wykonanych pomiarów z danymi katalogowymi, zmierzone widmo należało podzielić przez wzmocnienie układu, czyli przez 100. Porównanie uwzględniono na rysunku 13, wykres czarny to nasz pomiar analizatorem, wykres czerwony to naniesiona na tym rysunku na podstawie katalogu krzywa gęstości szumowej układu OP627. Jak widać, zgodność w zakresie szumu szerokopasmowego jest dość dobra, ale pomiary szumu 1/f odbiegają znacznie od danych katalogowych. Nasuwa się pytanie, jak parametry te są mierzone przez producenta lub co my zrobiliśmy nie tak? Być może pomiary do katalogów są prowadzone niemal w sterylnych warunkach, których my nie byliśmy w stanie zapewnić. Zauważmy na przykład, że szum termiczny stanowi znaczącą część wszystkich szumów. Zmiana temperatury choćby o pół stopnia może skutkować widoczną zmianą szumu. Nie bez znaczenia mogło być też napięcie zasilające. Parametry katalogowe są podawane dla napięcia zasilającego ± 15 V, gdy tymczasem w naszych pomiarach były używane baterie 9 V.
Obliczenia szumów na podstawie danych katalogowychI. Szum szerokopasmowy 1. Obliczenie wzmocnienia dla szumów
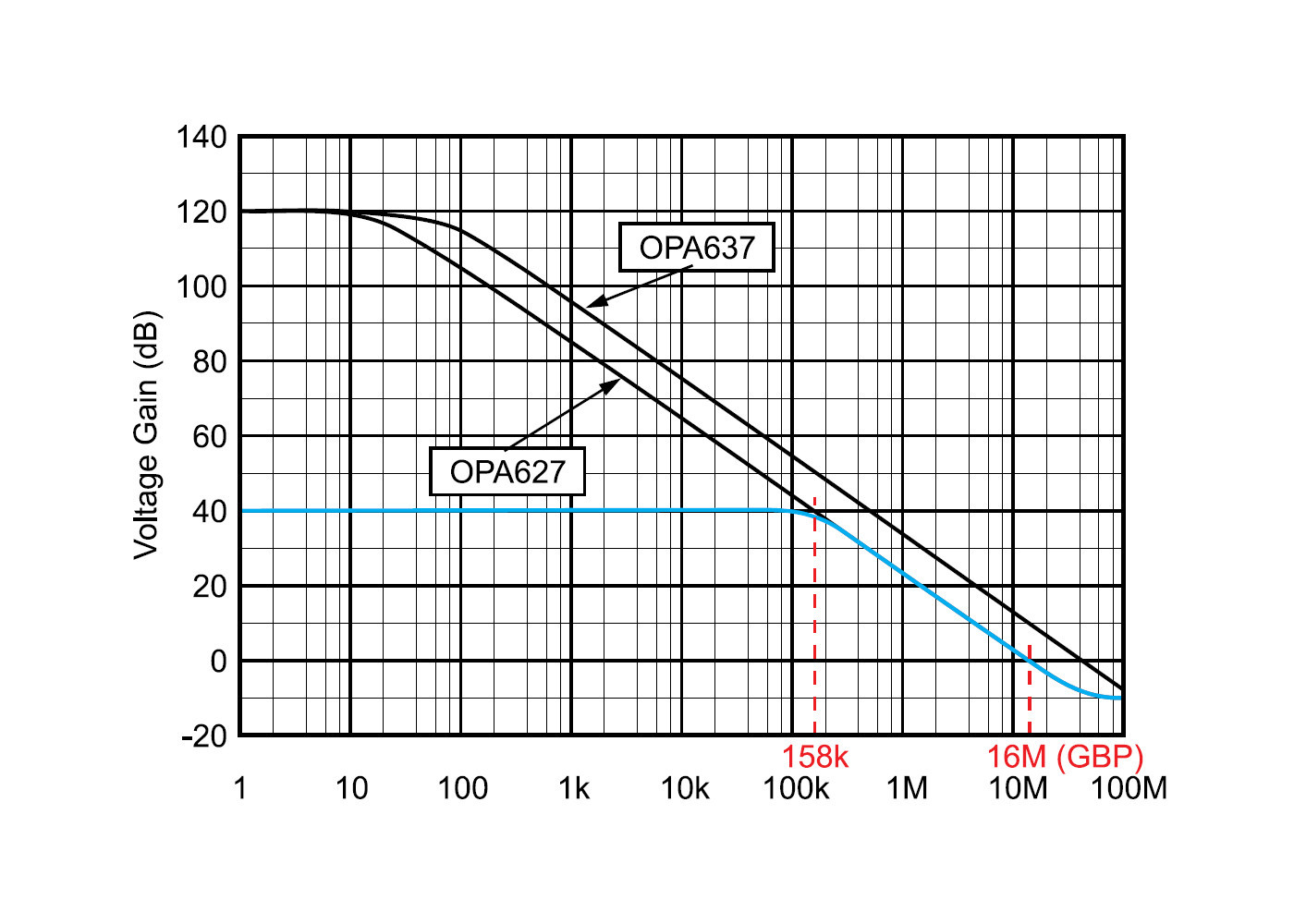
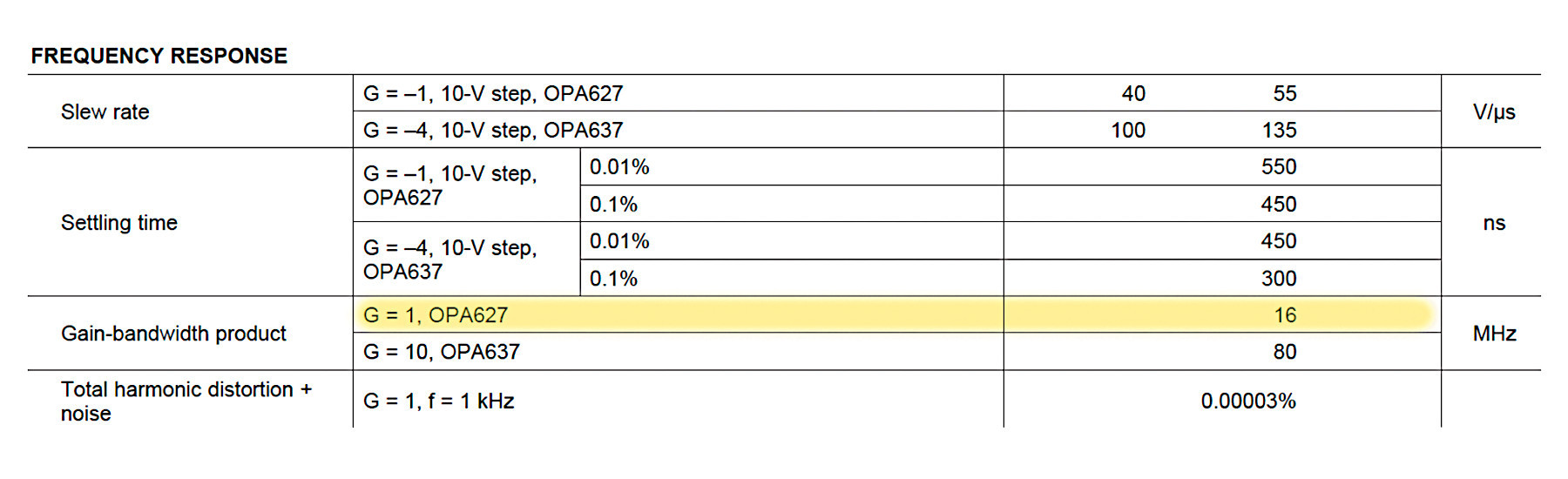
2. Obliczenie z wykresu (rys. 14 i rys. 15) lub na podstawie danych katalogowych częstotliwości dla wzmocnienia jednostkowego (Gain Bandwidth Product – GBP)
4. Obliczenie znormalizowanego pasma wzmacniacza BWn. Częstotliwość górna jest wyznaczona przez przemnożenie częstotliwości 3 dB (fn) przez współczynnik kn, który dla nachylenia charakterystyki 20 dB/dek jest równy 1,57
5. Obliczenie napięcia (RMS) szerokopasmowego szumu na podstawie wykresu wejściowej widmowej gęstości szumu układu OPA627 (rys. 16)
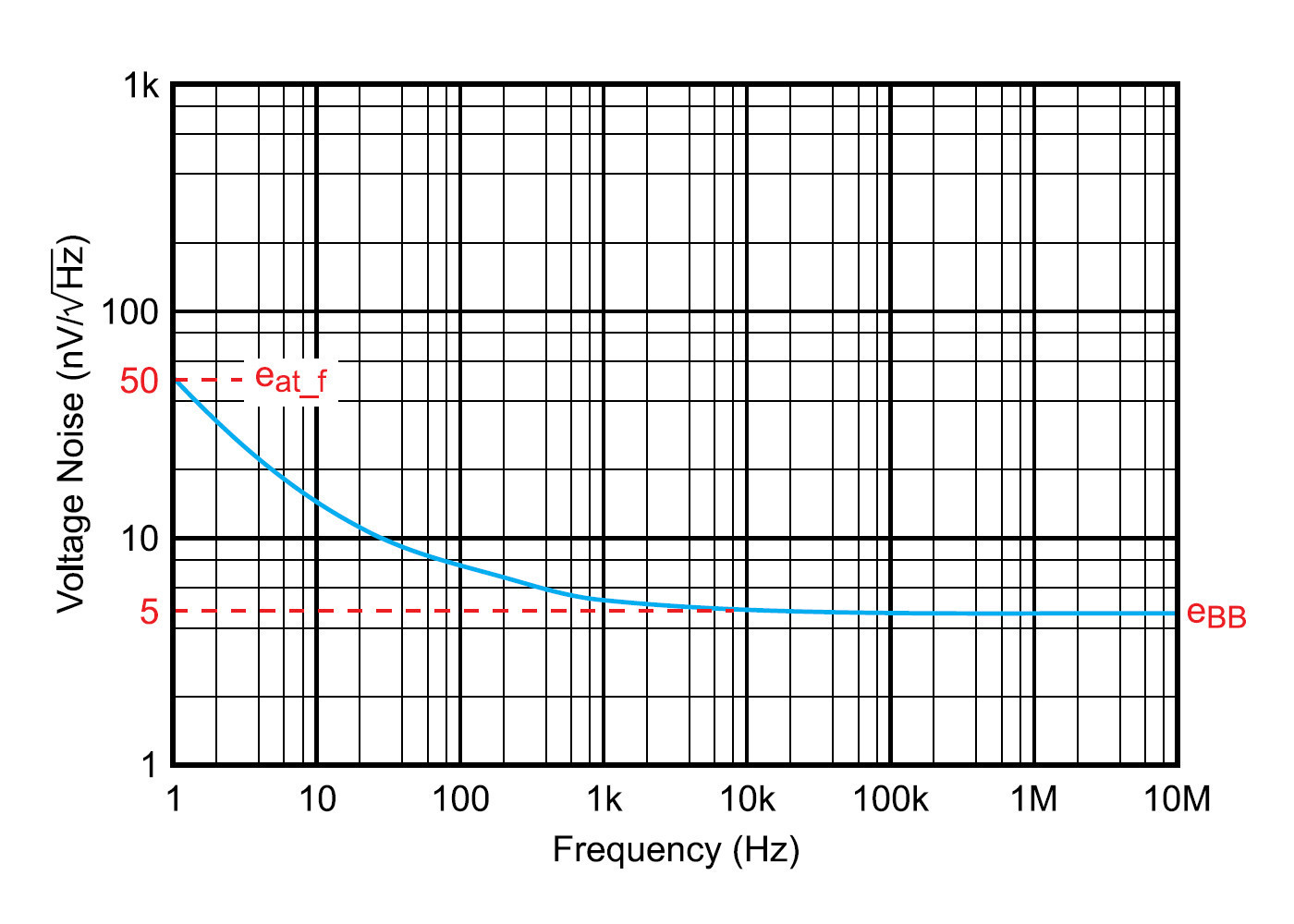
II. Szum 1/f 6. Obliczenie znormalizowanego szumu 1/f (efnorm) na podstawie parametrów odczytanych z wykresu (rys. 16). Korzystamy z odczytanej wartości eat_f np. dla częstotliwości 1 Hz. eat_f = 50 nV/√Hz
7. Obliczenie szumu 1/f. Jako parametry występują tu częstotliwości: fH – górna częstotliwość szumów i fL – dolna częstotliwość szumów (zwykle przyjmuje się 0,1 Hz).
8. Obliczenie całkowitego szumu napięciowego (1/f i szerokopasmowego).
III. Szum termiczny 9. Obliczenie rezystancji wypadkowej.
10. Obliczenie szumu termicznego generowanego przez rezystory
IV. Szum prądowy
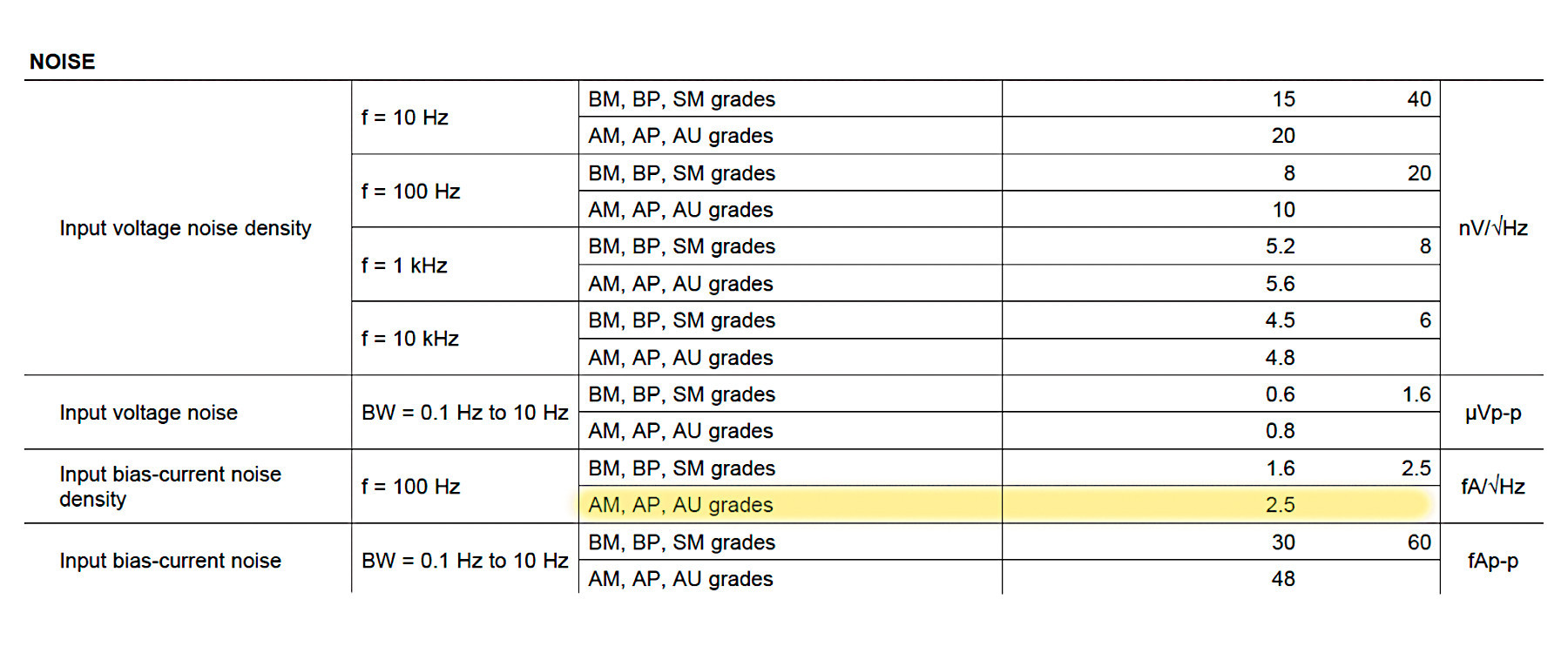
11. Obliczenie szerokopasmowego szumu prądowego na podstawie parametru input bias-current noise density (iBB) odczytanego z danych katalogowych układu OPA627 (rys. 17).
12. Obliczenie całkowitego szumu prądowego RMS. Poniższa równość wynika z faktu, że dla szumu prądowego nie występuje szum 1/f.
13. Obliczenie napięciowego szumu RMS odpowiadającego szumowi prądowemu dla rezystancji zastępczej
V. Obliczenie całkowitego szumu wyjściowego 14. Należy zauważyć, że wszystkie rozważane dotychczas rodzaje szumów są odnoszone do wejścia układu. Do obliczenia szumu wyjściowego potrzebny jest jeszcze całkowity szum wejściowy, który jest geometryczną sumą wszystkich obliczonych rodzajów szumu.
15. Obliczenie szumu wyjściowego. Jest on równy szumowi wejściowemu przemnożonemu przez wzmocnienie układu. Można powiedzieć, że to już koniec obliczeń, ale kto będzie mierzył wartość skuteczną szumu. Zwykle oglądając szum na oscyloskopie, oceniamy go na podstawie wartości peak-to-peak. Szum jest zjawiskiem losowym, dlatego trudno mówić o konkretnej wartości peak-to-peak. Na podstawie rozważań statystycznych można natomiast przyjąć, że do obliczenia napięcia międzyszczytowego szumu należy jego wartość RMS przemnożyć przez 6. Mamy wówczas 99,7% szansę wychwycenia wszystkich wartości szczytowych. Pozostaje więc wykonanie ostatniego kroku tego dość złożonego algorytmu.
16. Obliczenie całkowitego wyjściowego szumu peak-to-peak. |
Jarosław Doliński, EP