Metody obliczania rezystancji ścieżek i przelotek w obwodach drukowanych

Rezystancja połączeń ma szczególne znaczenie w przypadku coraz powszechniejszych obecnie układów o małej impedancji, gdzie spadek napięcia na elementach obwodu może poważnie zakłócić funkcjonowanie urządzenia. Warto zatem już na etapie projektowania podjąć próbę oszacowania wpływu mozaiki PCB na pracę układu, obliczając przewidywany spadek napięcia na liniach o krytycznym znaczenia dla funkcjonowania całego systemu.

Obliczanie spadku napięcia – prawo Ohma

Spadek napięcia na każdym elemencie układu, w tym również na ścieżkach i przelotkach, można wyliczyć w prosty sposób, korzystając bezpośrednio z prawa Ohma. Wynika z niego, że napięcie na elemencie jest równe iloczynowi natężenia przepływającego przez nie prądu oraz rezystancji elementu. Problemem może być jednak dokładne ustalenie rezystancji ścieżek oraz przelotek, ponieważ jej wartość zależy od stosunkowo dużej liczby czynników.

Rezystancja ścieżek oraz przelotek

Trudność w precyzyjnym wyznaczeniu wartości rezystancji ścieżek oraz przelotek wynika przede wszystkim z niedokładności rzeczywistych charakterystyk obwodu względem wielkości założonych przez projektanta lub podanych w specyfikacji producenta.

Parametrem o podstawowym znaczeniu jest rezystywność (opór właściwy) przewodnika, wyrażana w Ω×m. W związku z procesem technologicznym wytwarzania folii miedzianej rezystywność materiału w obrębie jednego arkusza może zmieniać się w zakresie do ok. 5%. Rezystywność zależy również w znacznej mierze od temperatury przewodnika. Temperaturowy współczynnik rezystancji miedzi (wyrażany w 1/°C) wynosi ok. 0,0038, zatem wraz ze wzrostem temperatury ścieżek, która zależy od temperatury otoczenia oraz natężenia płynącego przez nie prądu, rośnie ich rezystancja.

Kolejnym ważnym parametrem jest grubość warstwy przewodnika. W przypadku folii miedzianych wytyczne IPC dopuszczają tolerancję wartości jej grubości w zakresie nie większym niż 10%. W przypadku nakładania przewodnika w procesie metalizacji grubość warstwy miedzi na powierzchni płytki może zmieniać się znacznie bardziej, nawet do 50%.

Z powodu możliwych dość znaczących rozbieżności parametrów przewodnika precyzyjne obliczenie rezystancji ścieżki jest utrudnione. Z drugiej strony, również empiryczny pomiar tej wartości (zakładając, że płytka została już zaprojektowana i wykonana) może stanowić spore wyzwanie z powodu bardzo małej wartości mierzonej rezystancji.

Podstawową zależność pozwalającą wyliczyć rezystancję ścieżki przedstawia poniższe równanie.

R=ρ×L/A,

gdzie:
R – rezystancja ścieżki,
ρ – rezystywność materiału,
L – długość ścieżki,
A – powierzchnia przekroju poprzecznego przewodnika (iloczyn szerokości i grubości ścieżki).

Bezwzględna wartość rezystywności zmienia się w funkcji temperatury. Zazwyczaj w specyfikacjach podaje się wartość rezystywności materiału w określonej temperaturze odniesienia (typowo 20°C), zaś dla innych temperatur obliczeń należy już dokonać samodzielnie, korzystając z poniższej zależności.

ρ(T)=ρ(T_o)×(1+α_o×(T–T_o)),

gdzie:
T – temperatura przewodnika,
T₀ – temperatura odniesienia,
ρ(T) – rezystywność w określonej temperaturze,
ρ(T_o) – rezystywność w temperaturze odniesienia,
α_o – temperaturowy współczynnik rezystancji w temperaturze odniesienia.

Znając rezystancję ścieżki w temperaturze odniesienia, możliwe jest obliczenie rezystancji w określonej temperaturze za pomocą zmodyfikowanej wersji powyższego równania.

R(T)=R(T_o)×(1+α_o×(T–T_o)),

gdzie:
R(T) – rezystancja ścieżki w określonej temperaturze,
R(T_o) – rezystancja ścieżki w temperaturze odniesienia.

Praktyczny przykład obliczenia rezystancji ścieżki

Korzystając z powyższych zależności, obliczona zostanie rezystancja dla przykładowej ścieżki w dwóch wersjach – z przelotką umieszczoną na ścieżce oraz bez niej. Uzyskane wyniki porównane zostaną z rezultatami otrzymanymi z wykorzystaniem symulacji komputerowych.

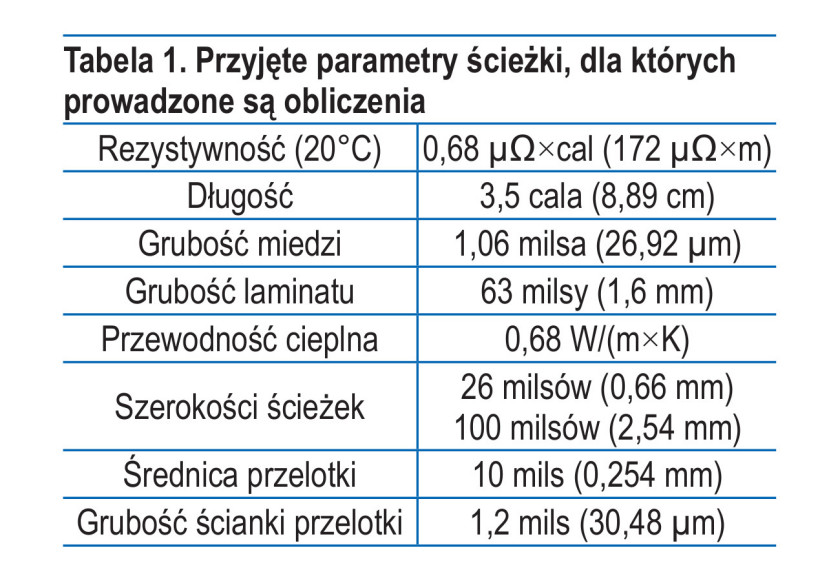
Przyjęte na potrzeby obliczeń parametry elementów obwodu przedstawiono w tabeli 1. Wymiary ścieżek oraz przelotek celowo dobrane zostały w taki sposób, aby powierzchnie przekroju poprzecznego tych elementów miały możliwie zbliżony rozmiar. W przypadku prowadzenia obliczeń bardzo ważne jest przyjęcie jednolitego układu jednostek miar. Decydując się na układ celowy, wartości wszystkich parametrów należy przeliczyć na cale lub milsy, decydując się na jednostki układu SI, należy korzystać z wartości wyrażonych w metrach i jednostkach pochodnych. Rezystancja ścieżki o szerokości 26 milsów w temperaturze 20°C wynosi:

R₂₀=0,68×3,5×10^–6/(26×1,06×10^–6)=0,0864 Ω

Po oszacowaniu natężenia prądu płynącego przez ścieżkę możliwe jest, z pomocą prawa Ohma, obliczenie występującego na niej spadku napięcia. Należy jednak, szczególnie przy wyższych natężeniach prądu, uwzględnić związany z tym wzrost temperatury ścieżki. Jeśli przez ścieżkę popłynie prąd o natężeniu 3,5 A, spowoduje to wzrost jej temperatury do ok. 83°C (do szacowania temperatury można użyć jednego z darmowych narzędzi do symulacji charakterystyk termicznych obwodu). Przy takiej temperaturze rezystancja ścieżki zmieni się następująco:

R₈₃=0,0864×(1+0,0038×(83 – 20))=0,1071 Ω

Zaś spadek napięcia w tej sytuacji wyniesie:

V₈₃=3×5×0,1071=0,37 V

Dla porównania, przy temperaturze 20°C spadek napięcia przy takim samym natężeniu prądu wyniósłby:

V₂₀=3,5×0,0864 =0,30 V

Można zatem zauważyć, że brak uwzględnienia wzrostu rezystancji przewodnika spowodowanego wzrostem temperatury prowadziłby do znaczącego przekłamania otrzymanego wyniku (0,07 V, czyli ok. 20%). Powyższy przykład uwzględnia dość skrajny przypadek, ponieważ większość projektantów stara się nie dopuszczać do tak wysokiego nagrzewania się ścieżek (powyżej 80°C), pozwala jednak uświadomić sobie wielkość potencjalnych zmian rezystancji obwodu związanych z nieprawidłowym zarządzeniem jego charakterystyką termiczną.

Dobrym sposobem na zmniejszenie rezystancji połączeń jest zwiększenie szerokości ścieżek. Zwiększając rozmiar ścieżki do 100 milsów, otrzymamy rezystancję:

R₂₀=0,68×3,5×10^–6/(100×1,06×10^–6)=0,0225 Ω

Zależność rezystancji ścieżki od jej szerokości jest liniowa, czyli czterokrotne zwiększenie szerokości pozwala czterokrotnie obniżyć rezystancję. Aby ścieżka o szerokości 100 milsów osiągnęła temperaturę zbliżoną do poprzedniego przykładu, musi przez nią płynąć prąd o natężeniu ok. 7,5 A (wzrost temperatury do 88°C). W takiej sytuacji rezystancja oraz spadek napięcia przedstawiają się następująco:

R₈₈= 0,0225×(1+0,0038×(88 – 20))=0,028 Ω
V₈₈=7,5×0,028=0,21 V

Wpływ przelotki na właściwości połączenia

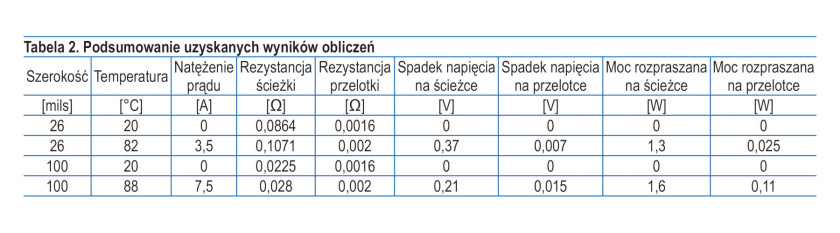
Przelotka o średnicy 10 milsów ma przekrój poprzeczny o powierzchni bardzo zbliżonej do ścieżki o szerokości 26 milsów i grubości 1,06 milsa. Dla celów obliczeń przelotkę taką można zatem zastąpić równoważnym modelem w postaci ścieżki o szerokości 26 milsów i długości 63 milsów (grubość laminatu). Korzystając z uprzednio przedstawionego sposobu obliczeń, uzyskamy rezystancję przelotki w temperaturze 20°C o wartości 0,0016 Ω. Przelotka wprowadza zatem do obwodu rezystancję o wartości równej jedynie 1,8% rezystancji ścieżki, czyli znacznie mniej niż wynosi wartość niepewności wyznaczenia parametrów wykorzystywanych do obliczeń. Temperatura przelotki zależy od temperatury ścieżki, zatem wraz ze wzrostem temperatury rezystancje obu tych elementów będą rosły proporcjonalnie – rezystancja przelotki wciąż będzie równa 1,8% rezystancji ścieżki. Spadek napięcia na przelotce dla prądu o natężeniu 3,5 A wyniesie ok. 7,0 mV (uwzględniając wzrost rezystancji przelotki wywołany temperaturą do ok. 0,002 Ω). Powyższe obliczenia pokazują, że akurat w tym przypadku zastosowanie przelotki ma pomijalnie niski wpływ na pracę układu. Podsumowanie uzyskanych wyników, znajduje się w tabeli 2.

Podsumowanie

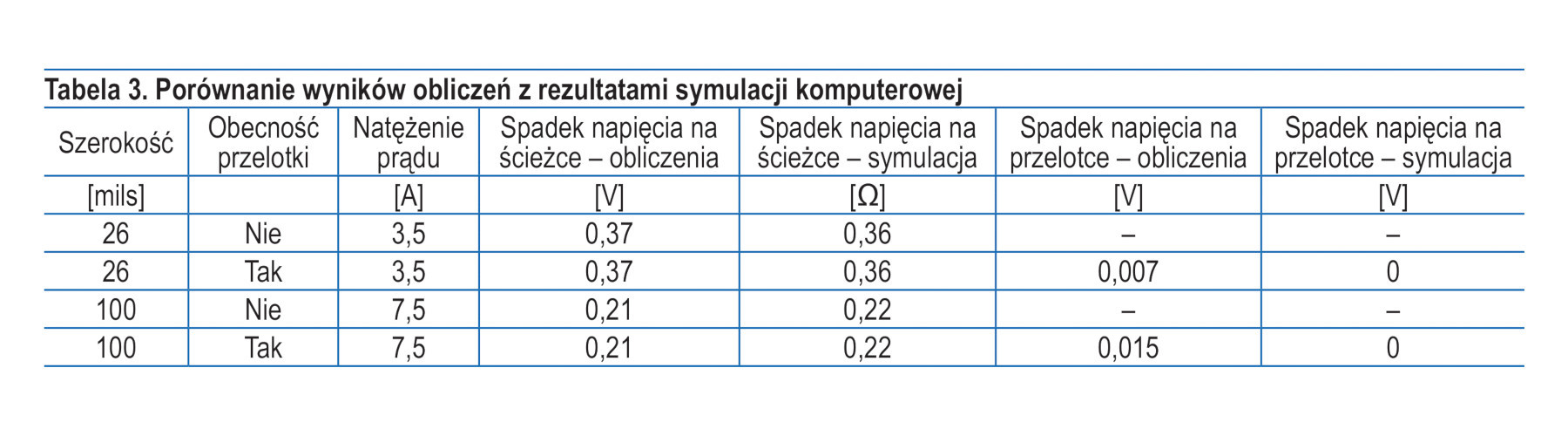
W tabeli 3 przedstawiono porównanie uzyskanych wyników obliczeń z rezultatami symulacji z wykorzystaniem narzędzi komputerowych (oprogramowanie Th ermal Risk Management Soft ware). Niemal identyczne wyniki udowadniają, że za pomocą prostych obliczeń możliwe jest samodzielne w miarę szybkie i dokładne oszacowanie spadku napięcia na wybranych elementach obwodu. Przeprowadzenie takich operacji, szczególnie w przypadku linii o krytycznym znaczeniu dla pracy układu, może już na etapie projektowania pozwolić na detekcję potencjalnych słabych punktów i źródeł późniejszej błędnej pracy systemu. Eliminacja ich już na tym etapie na pewno pozwoli zaoszczędzić czas oraz nakłady finansowe.

Damian Tomaszewski