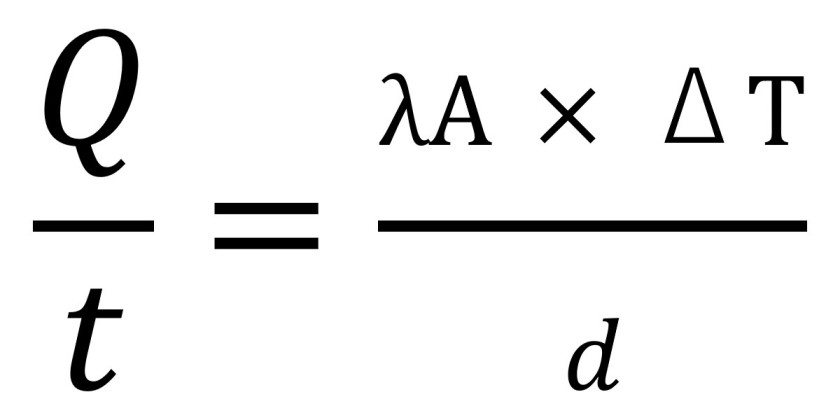Szacowanie temperatury ścieżek w obwodzie drukowanym

Zapewne wielu konstruktorów sądzi, że temperatura ścieżki zależna jest głównie od natężenia płynącego przez nią prądu elektrycznego oraz jej rezystancji. Pogląd taki powstać może po zapoznaniu się z równaniem opisującym wartość mocy rozpraszanej na elemencie obwodu, które wygląda następująco: P=I2R, gdzie P to moc, I to natężenie prądu, zaś R to rezystancja elementu.

Opinia taka nie jest w zasadzie błędna, z całą pewnością stanowi jednak znaczące uproszczenie. Jednostką mocy jest wat, określający ilość energii rozpraszaną w komponencie (na powierzchni ścieżki) w jednostce czasu. Może być zatem wyrażony w dżulach na sekundę (J/s). Ciągły proces dostarczania energii powinien zatem prowadzić do ciągłego wzrostu temperatury ścieżki, skutkując osiągnięciem nieskończonej jej wartości. W praktyce nie ma to jednak miejsca, ponieważ komponent (ścieżka) poddawany jest równocześnie procesowi chłodzenia, czyli odprowadzania nadmiaru ciepła do otoczenia.

Oddawanie ciepła odbywa się na trzy podstawowe sposoby – przez przewodnictwo, konwekcję oraz promieniowanie. W przypadku ścieżek obwodu PCB zjawiska konwekcji oraz promieniowania mają dość stabilny przebieg, raczej niezbyt zależny od czynników zewnętrznych oraz parametrów płytki. Dla projektanta obwodów znacznie bardziej interesujący jest proces przewodnictwa cieplnego, ponieważ może on być w istotny sposób modyfikowany przez odpowiednie zabiegi konstrukcyjne.

Wzór określający przewodnictwo cieplne dowolnego obszaru wykonanego z jednorodnego materiału ma następującą postać:

gdzie Q/t to tempo transferu energii cieplnej, wyrażane w dżulach/sekundę, λ to współczynnik przewodnictwa cieplnego, charakterystyczny dla materiału, z którego wykonano ścieżki, A to pole przekroju, przez który przepływa ciepło, ΔT to różnica temperatur pomiędzy najzimniejszym i najcieplejszym punktem obszaru (co wyznacza jednocześnie kierunek przepływu ciepła – od gorącego do zimnego punktu), w przypadku ścieżek jest to różnica pomiędzy temperaturą ścieżki a temperaturą dielektryka, d to odległość pomiędzy punktami, pomiędzy którymi ma miejsce przepływ ciepła.

Pracujący układ ma stałą wartość temperatury w sytuacji, gdy osiągnięta zostaje równowaga pomiędzy tempem nagrzewania (wyrażanym za pomocą równania I2R) oraz tempem chłodzenia, określanym przede wszystkim przez wzór opisujący przewodnictwo cieplne.

Sytuacja komplikuje się dodatkowo z powodu tego, że zarówno rozpraszana moc, jak i odprowadzane ciepło to wartości skalarne, charakterystyczne oraz poprawne jedynie dla danego punktu na powierzchni płytki oraz danego momentu w czasie. Rozkład tych parametrów zmienia się zarówno w funkcji położenia, jak i w funkcji czasu. Zmienność w czasie wynikać może m.in. ze zmiany wartości natężenia prądu oraz temperatury otoczenia. Zmiana w funkcji położenia spowodowana jest głównie niejednorodnymi właściwościami ścieżki, wynikającymi z niedokładności procesu produkcyjnego.

Zmienność w czasie

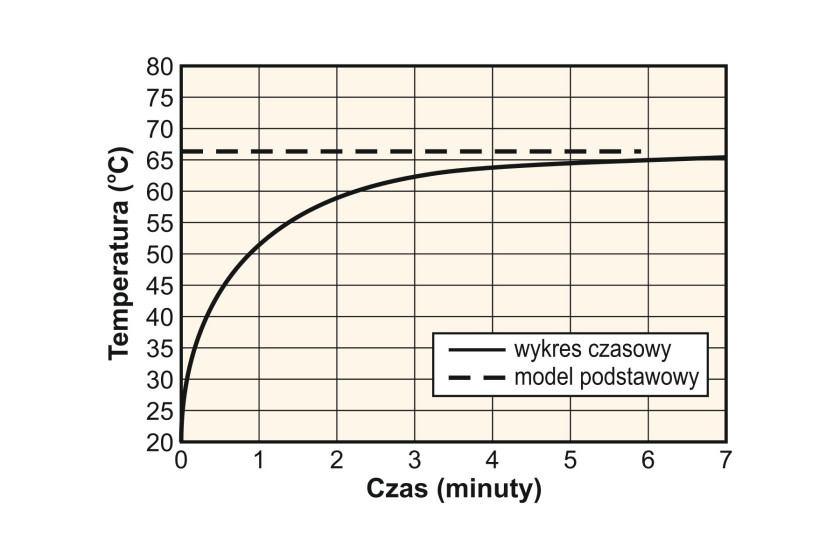
Jak wspomniano, opisane powyżej parametry i właściwości termiczne to wartości skalarne, właściwe dla określonego punktu w czasie. Ścieżka obwodu drukowanego, tak jak każdy obiekt fizyczny, charakteryzuje się pewną bezwładnością cieplną – jej temperatura rośnie w skończonym tempie, co pokazane zostało na rysunku 1. W większości przypadków osiągnięcie równowagi temperaturowej zajmuje od 5 do 10 minut. Czas też zależy w głównej mierze od poziomu przewodnictwa cieplnego materiału, z którego wykonana jest płytka.

 

Rys. 1. Temperatura ścieżki zmienia się w czasie – osiągnięcie stabilnej wartości dla określonego natężenia prądu wymaga zazwyczaj kilku minut

Wszystkie wykresy oraz symulacje przedstawione w tekście przeprowadzone zostały dla modelu opartego na prostokątnej płytce o wymiarach 50×200 mm, przez środek której biegnie pojedyncza ścieżka o długości 15 cm, zaś temperatura otoczenia podczas pracy układu wynosi 20°C. Zakłada się, że poziom promieniowania cieplnego oraz konwekcji utrzymuje się na stałym poziomie. Pozostałe istotne parametry modelu to:

• Szerokość ścieżki – 100 milsów
• Grubość ścieżki – 1,3 milsa
• Natężenie płynącego prądu – 8 A
• Opór właściwy przewodnika – 1,72 μΩ/cm
• Współczynnik przewodnictwa cieplnego dielektryka (w płaszczyźnie ścieżki) – 0,7
• Współczynnik przewodnictwa cieplnego dielektryka (prostopadle do płaszczyzny ścieżki) – 0,5
• Grubość płytki – 63 milsy

Gradient temperaturowy

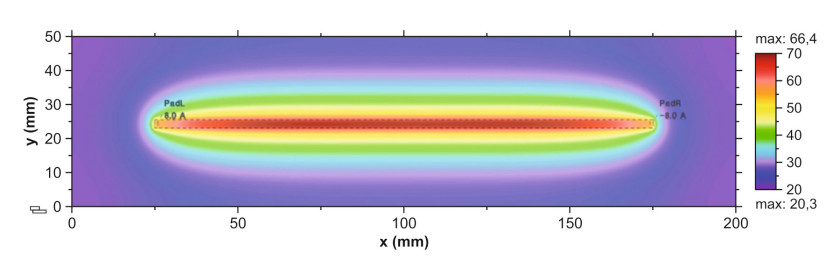
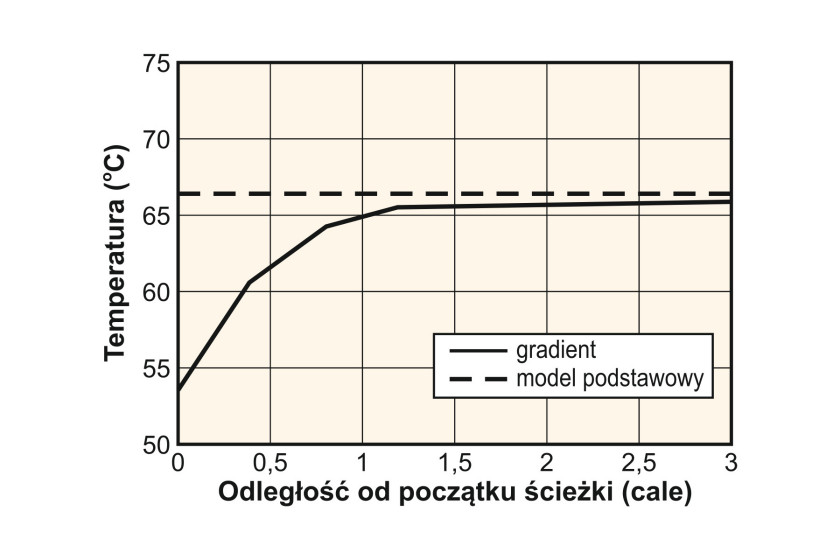
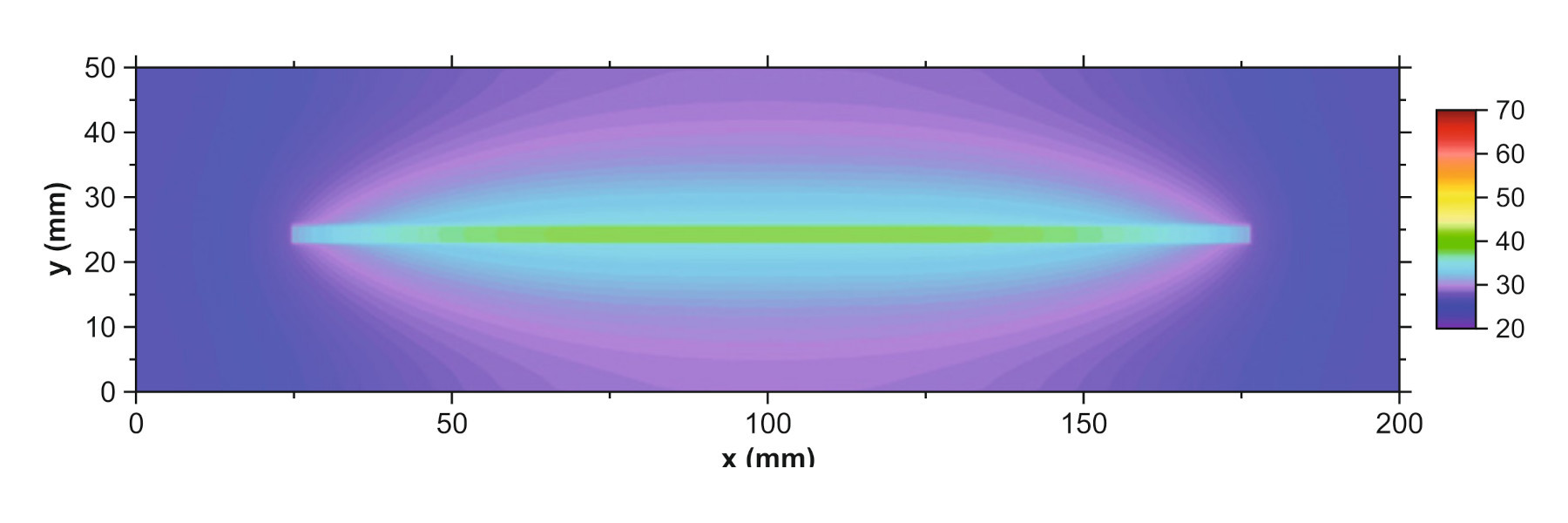
Na rysunku 2 przedstawiono rozkład temperatury wzdłuż powierzchni ścieżki, już po upływie czasu wymaganego do jej stabilizacji. Rozkład ten nie jest całkowicie równomierny – charakteryzuje się pewnym ochłodzeniem na końcach ścieżki, co jest typowe w przypadku większości obwodów drukowanych.

 

Rys. 2. Rozkład temperatury wzdłuż ścieżki charakteryzuje się zazwyczaj pewnym ochłodzeniem na jej końcach

Przyczyną tego zjawiska jest fakt, że na zakończeniach ścieżek znajdują się zazwyczaj większe obszary przewodnika – pola lutownicze, pady, przelotki lub inne płaszczyzny wykonane z miedzi. Pełnią one funkcję zbliżoną do roli radiatora – zwiększają tempo odprowadzania ciepła z przylegających do nich obszarów przewodnika, skutecznie obniżając w ten sposób temperaturę ścieżki. Skuteczność chłodzenia maleje wraz ze wzrostem odległości, przez co obszary bardziej oddalone (środkowa część ścieżki) charakteryzują się wyższą temperaturą.

 

Rys. 3. Rozkład temperatury wzdłuż ścieżki nie jest jednorodny – w pobliżu padów/pól lutowniczych temperatura zauważalnie maleje

Grubość płytki

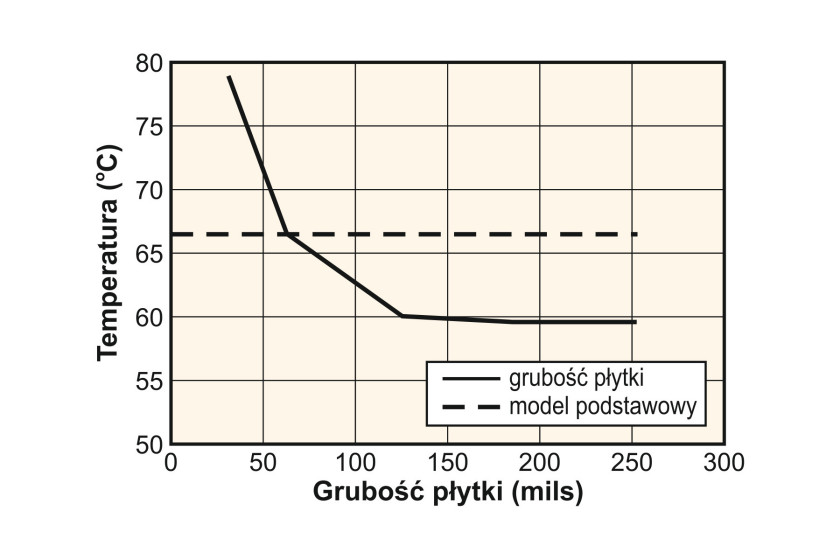
Temperatura ścieżki dość istotnie zależy od grubości płytki drukowanej. Ścieżki umieszczone na płytce o większej grubości charakteryzować się będą niższą temperaturą podczas pracy. Wraz ze wzrostem grubości zwiększa się ilość materiału pochłaniającego ciepło wydzielane przez płytkę, rośnie zatem efektywność procesu odprowadzania ciepła oraz chłodzenia ścieżek. Nie jest to jednak zależność liniowa – powyżej pewnego progu dalsze zwiększanie grubości płytki nie przynosi już zauważalnych rezultatów, co przedstawione zostało na rysunku 4.

 

Rys. 4. Temperatura ścieżek zależy od grubości płytki. Wraz ze wzrostem grubości temperatura maleje, nie jest to jednak zależność liniowa

Jak pokazują wyniki symulacji, zmiana grubość płytki w badanym modelu z 63 do 32 milsów powoduje zwiększenie temperatury ścieżki z 66,4°C do 78,9°C. Dwukrotne zwiększenie grubości płytki (do 126 milsów) powoduje spadek temperatury do wartości ok. 60°C, jednak dalsze zwiększanie grubości nie powoduje już znaczących rezultatów.

Współczynnik przewodzenia ciepła

Każdy materiał charakteryzuje się określoną wartością współczynnika przewodzenia ciepła λ, opisującego zdolność do przekazywania energii wewnętrznej i wyrażanego w [W/(m·K)]. W tych samym warunkach większa ilość energii cieplnej przepłynie przez substancję o większej wartości współczynnika λ.

W przypadku dielektryków wartość współczynnika λ wynosi zazwyczaj od ok. 0,3 do ok. 0,8. Dla porównania, w przypadku miedzi jest to ok. 350. Na rynku pojawiają się nowe materiały przeznaczone do konstrukcji obwodów drukowanych, cechujące się znacząco większymi wartościami współczynnika λ, co pozwala na zauważalną poprawę charakterystyki termicznej układów.

 

Rys. 5. Przepływ ciepła przez płytkę PCB zależy od kierunku przepływu względem ułożenia warstw płytki

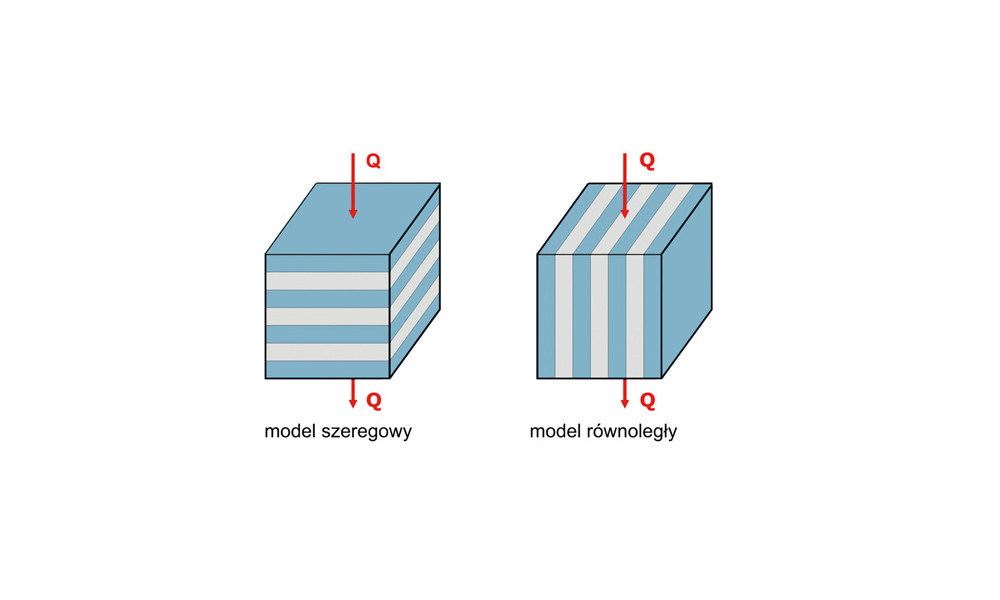
Płytka PCB jest konstrukcją składającą się zazwyczaj z kilku połączonych ze sobą warstw materiału. Z tego też powodu przepływ ciepła przez jej strukturę nie jest jednorodny – jego charakterystyka zmienia się w zależności od kierunku. W teorii problem ten opisywany jest jako przepływ ciepła w materiałach wielofazowych. Wypadkowy współczynnik ciepła zależy od kierunku przepływu względem sposobu ułożenia warstw materiału.

W przypadku płytek PCB w danych technicznych znaleźć można niekiedy dwie różne wartości współczynnika λ in-plane, czyli równolegle do płaszczyzny ścieżek oraz through-plane, czyli prostopadle do płaszczyzny ścieżek. Płytki PCB charakteryzują się zazwyczaj lepszym przewodnictwem w przypadku przepływu ciepła równoległego do płaszczyzny ścieżek.

Temperatura ścieżek silnie zależy od wartości współczynnika λ. W przypadku badanego modelu obniżenie wartości λ inplane z 0,7 do 0,6 powoduje wzrost temperatury ścieżki o 4,3°C – z 66,4°C do 70,7°C. Obniżenie wartości λ through-plane z 0,5 do 0,4 powoduje zaś wzrost temperatury o 0,8°C, do 67,2°C. Można zatem zauważyć, że wartość λ in-plane ma znacznie większy wpływ na końcową temperaturę ścieżek i charakterystykę termiczną układu.

 

Rys. 6. Temperatura ścieżki znacząco maleje po umieszczeniu w jej pobliżu płaszczyzny przewodnika

Wymiary ścieżek

Obawy dotyczące zbyt wysokiej temperatury dotyczą zazwyczaj ścieżek, przez które przepływa duża moc. Wiedząc o dużym natężeniu przepływającego prądu, projektanci starają się nadać takim ścieżkom odpowiednią szerokość. Z tego względu okazuje się, że względna niedokładność szerokości tego typu ścieżek wynikająca z procesu produkcyjnego jest raczej niewielka – nie wpływa znacząco na rozkład temperatury wzdłuż powierzchni ścieżki.

Inaczej wygląda jednak sytuacja związana z grubością ścieżki. Grubość warstwy przewodnika tworzącej ścieżkę jest za zwyczaj o kilka rzędów wielkości mniejsza od jej szerokości – nawet niewielkie lokalne różnice tej wartości związane ze skończoną dokładnością procesu produkcyjnego mogą przełożyć się na znaczące zmiany rozkładu temperatury obwodu. W przypadku typowego obwodu drukowanego grubość ścieżki charakteryzuje się zmiennością w zakresie wartości rzędu dziesiątych części milsa, co może oznaczać zmianę nawet o kilkadziesiąt procent w stosunku do nominalnej wartości.

Zmiana grubości ścieżki ma istotny wpływ na jej temperaturę. W przypadku prezentowanego modelu spadek grubości z 1,3 do 1,2 milsa powoduje wzrost temperatury o 4,4°C, do 70,8°C (wzrost o 6,6%).

Rodzaj przewodnika

Warstwę przewodnika w obwodzie drukowanym wykonuje się zazwyczaj z jednego z dwóch rodzajów miedzi: folii miedzianej osadzanej elektrycznie (plated copper) lub miedzi walcowanej (rolled copper). Skład miedzi osadzanej elektrycznie jest z reguły bardziej zbliżony do czystej miedzi. Jej opór właściwy wynosi ok. 1,64 μΩ/cm.

Miedź walcowana powstaje w procesie wyżarzania. Jej opór właściwy zmienia się w zależności od rodzaju materiału, zazwyczaj wynosi jednak ok. 1,72 μΩ/cm. Opór właściwy miedzi ma bezpośredni wpływ na rezystancję ścieżki, przez to zaś na poziom rozpraszanej na niej mocy. Zmiana materiału wykorzystywanego do budowy ścieżek z miedzi walcowanej na miedź osadzaną elektrycznie prowadzi zatem do obniżenia temperatury układu. W przypadku omawianego modelu zmiana taka spowoduje spadek temperatury o 3°C.

Obecność płaszczyzn przewodnika

Większość współcześnie wykonywanych wielowarstwowych obwodów drukowanych zawiera w swojej strukturze płaszczyzny przewodnika, mogące pełnić np. funkcję płaszczyzny masy lub zasilania. Obecność takiej płaszczyzny również wywiera istotny wpływ na rozkład temperatury ścieżek – współczynnik przewodnictwa cieplnego λ przewodnika jest kilkusetkrotnie wyższy niż w przypadku laminatu wykorzystywanego do budowy płytki. Ciepło może zostać odprowadzone do takiej płaszczyzny, następnie zaś równomiernie rozprowadzone na całej jej powierzchni. Płaszczyzny takie pełnią zatem funkcję zbliżoną do radiatora.

Jeśli w przypadku omawianego modelu po przeciwnej stronie płytki umieszczona zostanie płaszczyzna masy, temperatura ścieżki spadnie z 66,4°C do 45,2°C. Jeśli płaszczyzna taka umieszczona zostałaby nieco bliżej ścieżki (np. jako warstwa wewnętrzna płytki), 12 milsów poniżej warstwy ścieżki, to temperatura spadnie jeszcze bardziej, do 38,1°C. Sytuacja taka pokazana została na rysunku 6. Porównując to do rysunku 2, obrazującego pierwotny rozkład temperatury wzdłuż ścieżki, zauważyć można istotnie większą powierzchnię rozpraszania ciepła, skutkującą tak znaczącym obniżeniem temperatury.

Podsumowanie

Temperatura ścieżek w obwodzie drukowanym zależy od wielu czynników, takich jak rodzaj materiału wykorzystywanego do konstrukcji ścieżki oraz płytki, wymiarów ścieżki, obecności w pobliżu innych obszarów przewodnictwa, a także parametrów płynącego przez ścieżkę sygnału.

Tak duża liczba czynników wpływających na końcową wartość temperatury znacząco utrudnia oszacowanie tej wartości. W praktyce niemal niezbędne staje się zatem korzystanie z narzędzi komputerowych pozwalających na symulację oraz modelowanie właściwości temperaturowych obwodu. Uważna analiza tego typu danych pozwala na detekcję oraz korektę potencjalnie niebezpiecznych punktów układu, mogących prowadzić do jego przegrzania a w konsekwencji uszkodzenia.

Damian Tomaszewski