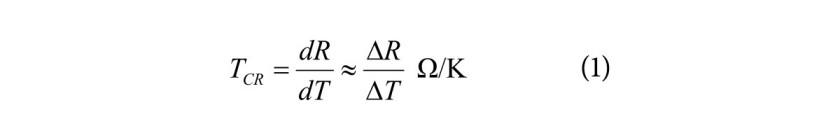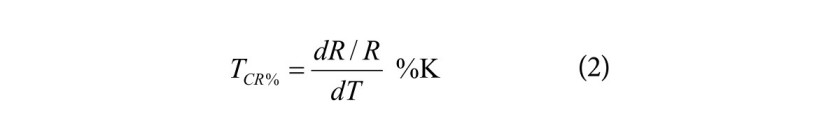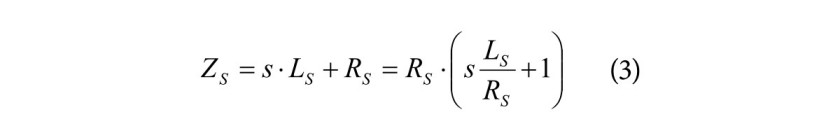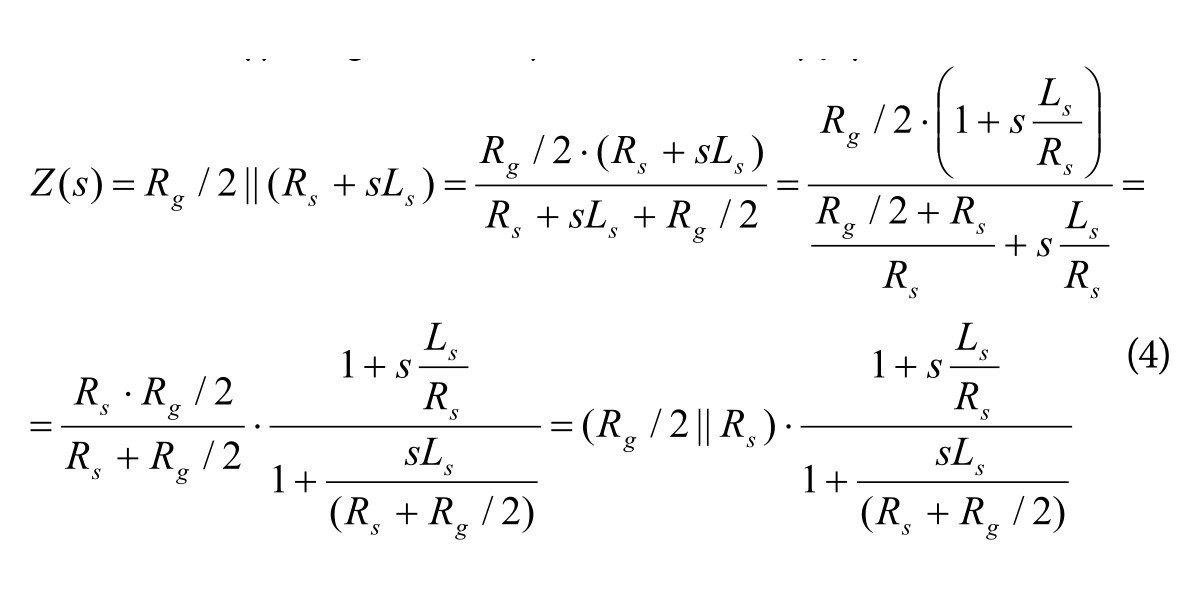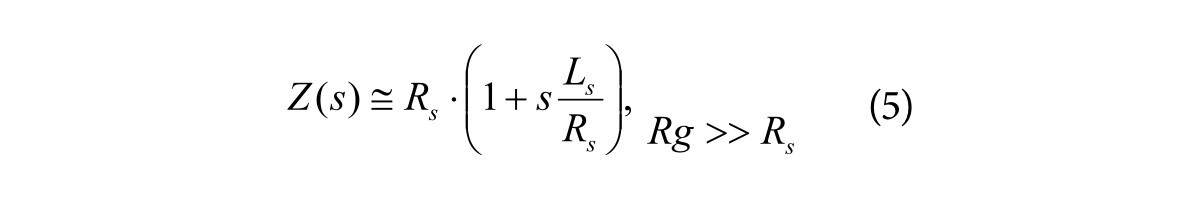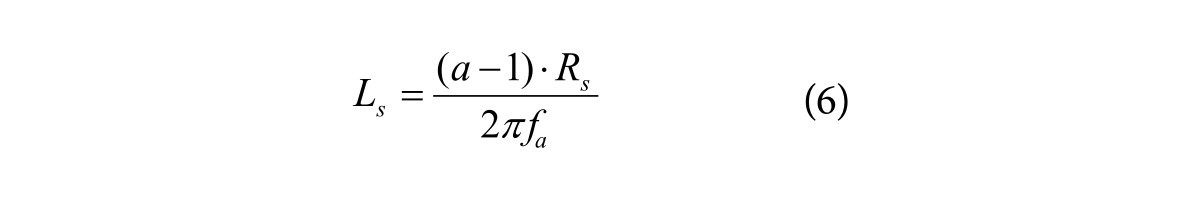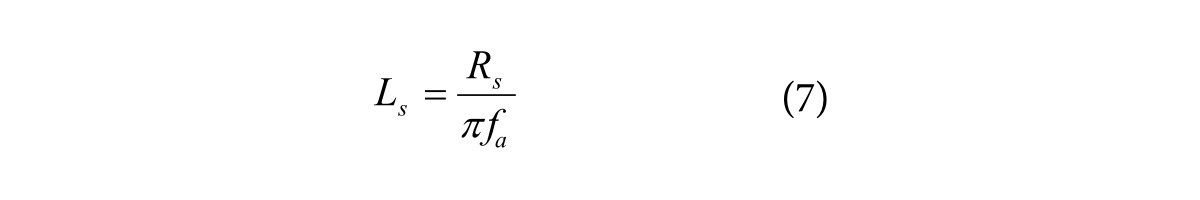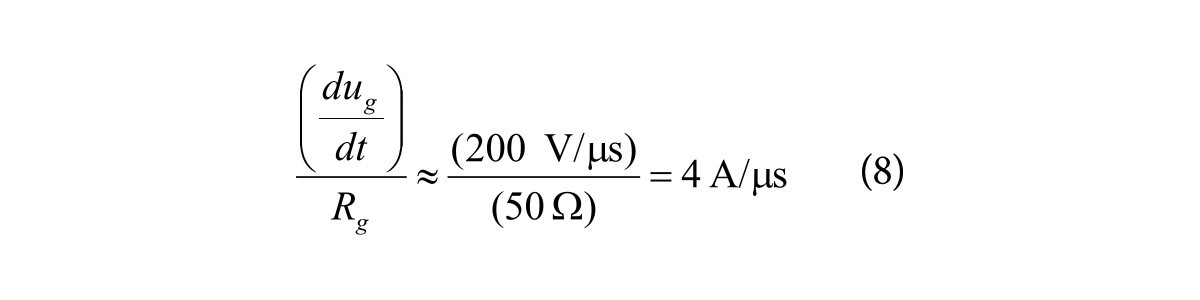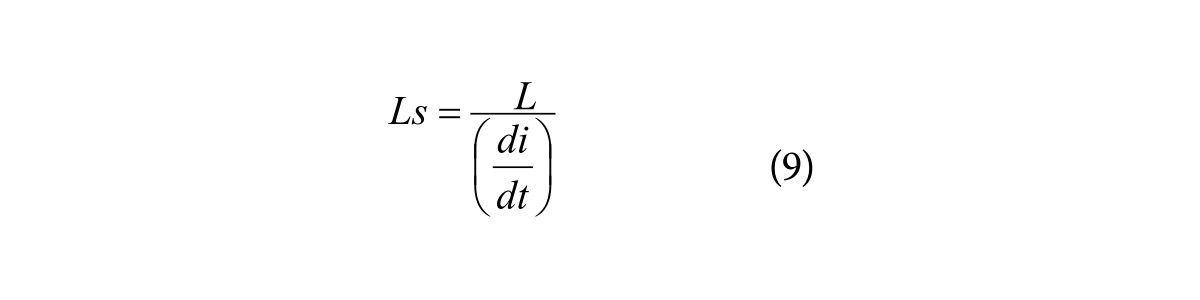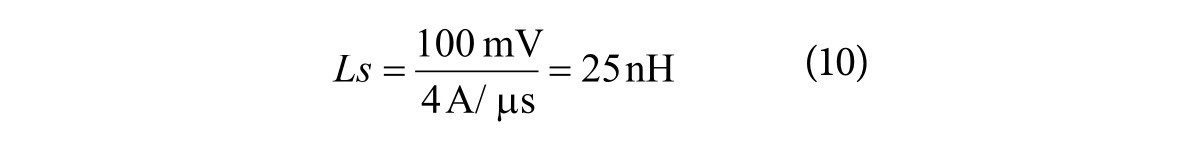Niuanse pomiarów rezystancyjnych czujników prądu
| TechnikaUkład elektroniczny o dużym stopniu złożoności składa się z wielu elementów, bloków funkcjonalnych, modułów itp. Pełnią one różne funkcje, jedne mniej, inne bardziej istotne z punktu widzenia działania urządzenia. Do najważniejszych z pewnością należy zaliczyć takie elementy jak mikroprocesory czy tranzystory wyjściowe kocówek mocy. Czasami jednak niemalże kluczową rolę w układzie odgrywają elementy niewielkie i niepozorne, choćby takie jak rezystory służące do pomiaru prądu.
Dwie podstawowe wielkości elektryczne mierzone rutynowo przez elektryków i elektroników to napięcie i natężenie prądu. Z technicznego punktu widzenia pomiar napięcia nie stanowi żadnego problemu, wystarczy przyłożyć dwie końcówki pomiarowe do punktów, pomiędzy którymi to napięcie występuje i odczytać gotowy wynik na wskaźniku przyrządu. Przy zachowaniu warunku, że rezystancja wewnętrzna woltomierza jest wielokrotnie większa od rezystancji obwodu mierzonego, rozpływ prądu do woltomierza, może być zaniedbany, a to prowadzi do wniosku, że pomiar nie jest obarczony istotnym błędem. Znacznie trudniej wygląda pomiar natężenia prądu, gdyż konieczne jest przerwanie obwodu i umieszczenie w nim rezystora pełniącego funkcję czujnika prądu. Istnieją wprawdzie metody, np. indukcyjne, niewymagające ingerencji w obwód mierzony, ale nadal konieczne jest wydzielenie pojedynczego przewodu, na który nałożone by były cęgi pomiarowe. W obwodzie drukowanym jest to praktycznie niewykonalne. Pomijamy przy tym liniowość i dokładność pomiaru.
W wielu aplikacjach pomiar prądu płynącego w obwodzie jest konieczny do zapewnienia prawidłowego działania układu. Dobrym przykładem są końcówki mocy, w których kluczową rolę odgrywają rezystory używane do pomiaru i stabilizacji prądu. Będziemy je nazywać dalej rezystorami czujnikowymi (ang. sense resistor). Aby rezystor czujnikowy nie oddziaływał na układ mierzony, powinien mieć jak najmniejszą rezystancję. Z oczywistych względów nie można jednak schodzić poniżej pewnego minimum. Po pierwsze, wiązałoby się to z koniecznością stosowania układów pomiarowych o dużym wzmocnieniu, po drugie, coraz bardziej odczuwalne by były szumy oraz rezystancje pasożytnicze. Nie można też zupełnie ignorować rezystancji doprowadzeń i styków.
Wpływ temperatury na rezystancję rezystorów czujnikowych
Temperatura jest tą wielkością fizyczną, która mocno utrudnia pracę konstruktorom urządzeń elektronicznych. Wpływa w istotny sposób m.in. na zmiany rezystancji rezystorów czujnikowych. Ilościowo efekt ten jest wyrażany współczynnikiem temperaturowym TCR:
lub w formie procentowej:
W idealnym przypadku oba współczynniki są równe zero. Producenci rezystorów dążą do opracowania takich technologii, które zapewniałyby jak najniższy TCR, a konstruktorzy urządzeń opracowują metody kompensacji wpływu temperatury na rezystancje użytych rezystorów.
Współczynnik temperaturowy
Rezystory czujnikowe w obwodach mocy same również rozpraszają sporą moc, a co za tym idzie, ulegają samonagrzewaniu. Zwykle są to elementy o mocy znamionowej od 0,5 do 5 W. Ze względu na funkcję, którą pełnią w układzie, ich rezystancja nie powinna się jednak zmieniać, gdyż prowadziłoby to do błędów pomiaru prądu. Ważne jest zatem, żeby były to elementy o jak najmniejszym współczynniku temperaturowym.
Rozważmy przykład, w którym rezystor czujnikowy jest wykonany w postaci odpowiednio przyciętego odcinka drutu miedzianego i jest zastosowany do pomiarów prądu silnika. Gdyby taki układ nie był prawidłowo skompensowany, zmiana rezystancji rezystora czujnikowego powodowałaby błąd pomiaru prądu, a to z kolei skutkowałoby zmniejszaniem się momentu obrotowego silnika.
Nie można jednak zbyt pochopnie przesądzać o tym, że przedstawiona metoda pomiaru prądu jest całkowicie bezużyteczna. Współczynnik temperaturowy miedzi jest prawie stały w szerokim zakresie temperatur, a jego dodatnia wartość wynosząca ok. 0,4%/°C może być łatwo kompensowana ujemnym współczynnikiem złącza półprzewodnikowego równym –0,2 mV/°C.
Rezystory czujnikowe stosowane w praktyce
Rezystory czujnikowe mogą być z powodzeniem wykonane we własnym zakresie, wystarczy użyć materiału przewodzącego o niskim współczynniku TCR. Do wykonania takiego rezystora nie jest wymagany ani specjalistyczny sprzęt, ani nieprzeciętne umiejętności. Redukowany do minimum jest przy tym koszt wytworzenia rezystora. Materiałem wyjściowym może być drut manganinowy, będący stopem miedzi, manganu i niklu. Charakteryzuje się on współczynnikiem TCR równym 15 ppm/K w zakresie temperatury od 0°C do 80°C. Drut manganowy o rozmiarze 18 AWG (średnica 1,024 mm, przekrój 0,0403 mm²) ma rezystywność 0,361 Wm. Drut o tej średnicy i cieńszy jest do nabycia w rolkach. Wykonanie rezystora czujnikowego jest banalnie proste, wystarczy odmierzyć i przyciąć odpowiedni odcinek drutu, ocynować końcówki, a następnie przylutować do płytki. Przykładowe rozwiązanie zostało pokazane na fotografii 1. Rezystor ma oporność 25 mW, ale należy też zwrócić uwagę na jego kształt. Dzięki zastosowaniu półpętli uzyskano minimalizację indukcyjności własnej. Dla porównania na fotografii 1b i 1c pokazano jednoprocentowe rezystory fabryczne. Do ich produkcji została zastosowana folia metalowa o niskim współczynniku temperaturowym naniesiona na anodyzowane podłoże aluminiowe.
Innym często stosowanym materiałem o niskim współczynniku temperaturowym jest nichrom (chromonikielina). Rezystywność tego stopu jest równa 133 mWcm. Pozwala to wykonywać rezystory z użyciem krótszych odcinków drutu w porównaniu z rezystorami manganinowymi. Rezystywność tego stopu jest równa 43 mWcm. Krótszy drut oznacza z kolei mniejszą indukcyjność własną. Na tym kończy się przewaga nichromu nad manganinem, bo przegrywa rywalizację pod względem współczynnika temperaturowego i stabilności rezystancji.
Rezystory czujnikowe z kelwinowskimi wyprowadzeniami
W aplikacjach pomiarowych, w których są stosowane rezystory o małych opornościach, na przykład w układach pomiaru prądu z rezystorami czujnikowymi, występuje problem wpływu rezystancji przewodów zasilających na wynik pomiaru. Rozwiązaniem jest stosowanie połączeń czteroprzewodowych, tzw. kelwinowskich. Taki rodzaj połączeń jest często stosowany w różnych aplikacjach pomiarowych, może też być użyty do pomiarów prądu z rezystorami czujnikowymi. Jedną parą przewodów doprowadzany jest prąd do czujnika, druga para zaś służy do pomiaru spadku napięcia na rezystancji czujnika. Rezystory czujnikowe z wyprowadzeniami kelwinowskimi można kupić jako gotowe wyroby (fot. 2). Mogą być one również wykonane jako elementy obwodu drukowanego, w postaci odpowiednio zaprojektowanych ścieżek. Jest to najtańsza metoda wytworzenia rezystorów czujnikowych, ale wymagana jest w tym przypadku kompensacja współczynnika temperaturowego z użyciem złącza krzemowego.
Pasożytnicza indukcyjność szeregowa
Rezystory czujnikowe są często umiejscawiane w pętli sterowania ze sprzężeniem zwrotnym. Obwody takie charakteryzują się własną dynamiką, która nie może być zaburzona włączeniem dodatkowego elementu, jakim jest rezystor czujnikowy. Końcówki doprowadzające prąd do rezystora stanowią element indukcyjny. Jest to uwidocznione w modelu zastępczym rezystora czujnikowego poprzez umieszczenie w nim szeregowej indukcyjności pasożytniczej. W układach stałoprądowych lub niskoczęstotliwościowych indukcyjność ta nie ma większego znaczenia, gdyż związana z nią stała czasowa jest bardzo mała. Jednak, gdy maleje również rezystancja, stała czasowa t=L/R może wzrosnąć na tyle, że opadanie charakterystyki częstotliwościowej zaczyna się w zakresie charakterystyki pętli, prowadząc do zaburzenia jej dynamiki.
Stwierdzenie istnienia pasożytniczej indukcyjności doprowadzeń rzędu 50 nH do 200 nH jest względnie proste, chociaż zastosowanie typowych mostków RLC mogłoby nie dać pozytywnych wyników. Dużo lepsza okazuje się metoda oscyloskopowa. Przykładowo: rezystor czujnikowy o oporności 100 W i indukcyjności wyprowadzeń 100 nH charakteryzuje się stałą czasową 1 ms. Rezystor 10 mW będzie miał stałą czasową 10 ms, co odpowiada częstotliwości granicznej ok. 16 kHz. Z kolei częstotliwość 16 kHz może mieścić się w zakresie pasma pętli sprzężenia zwrotnego wielu obwodów mocy, w których mierzony jest prąd. Schemat zastępczy rezystora czujnikowego jest opisami zależnością zapisaną rachunkiem operatorowym:
Widoczne w tym wyrażeniu zero wZ=1/(sLS/RS) wprowadza kolejny biegun w odpowiedzi wzmacniacza prądowego w zamkniętej pętli, jeśli znajdzie się w obwodzie sprzężenia zwrotnego. Z tego względu nie wolno ignorować tego parametru.
Pomiar indukcyjności pasożytniczej rezystora czujnikowego metodą przemiatania częstotliwości
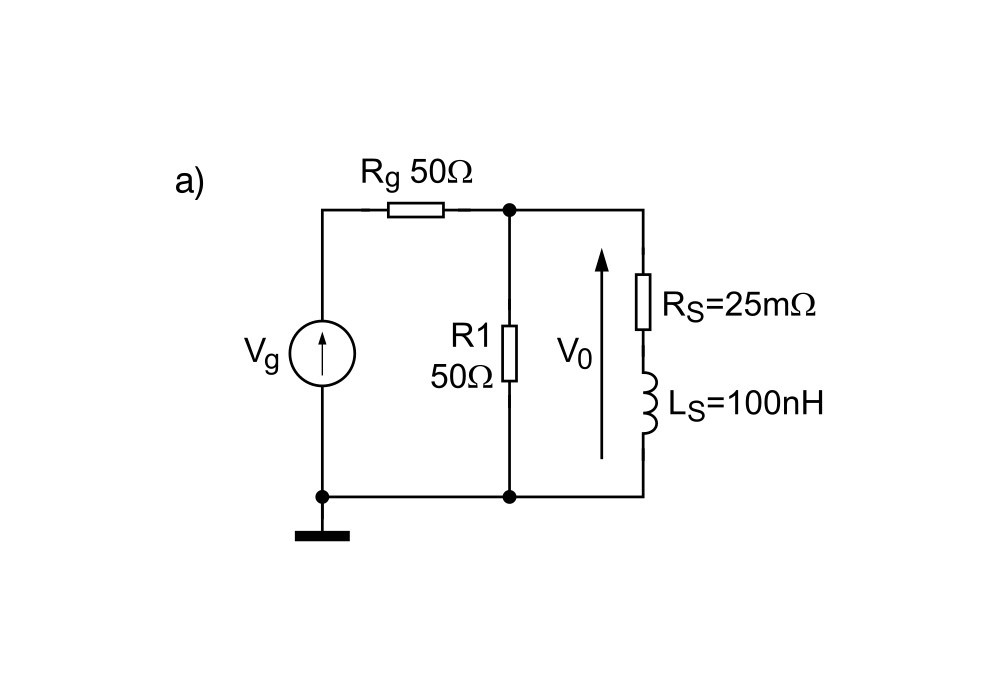
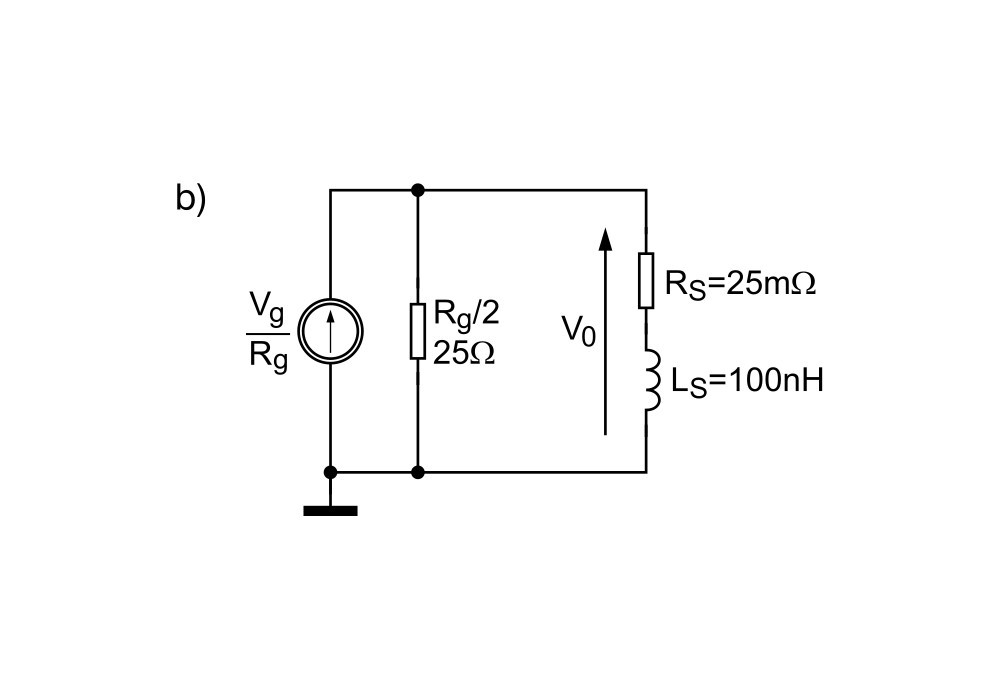
Pomiar indukcyjności pasożytniczej rezystora czujnikowego może być wykonany przy użyciu prostego układu (rys. 3a), który można zmontować dosłownie w pięć minut. Układ zawiera generator sygnału sinusoidalnego i rezystor 50 W (R1). Jego oporność została dopasowana do typowej oporności wyjściowej generatorów równej właśnie 50 W. Schemat z rysunku 3a został przekształcony do postaci z rysunku 3b. Źródło napięciowe zostało zastąpione źródłem prądowym, co jest wygodniejsze ze względu na dalszą analizę. Na schemacie z rys. 3b uwzględniono rezystor terminujący R1, który w połączeniu z rezystancją generatora o tej samej oporności utworzył rezystancję zastępczą 25 W. Impedancja układu widziana z wyjścia generatora jest równa:
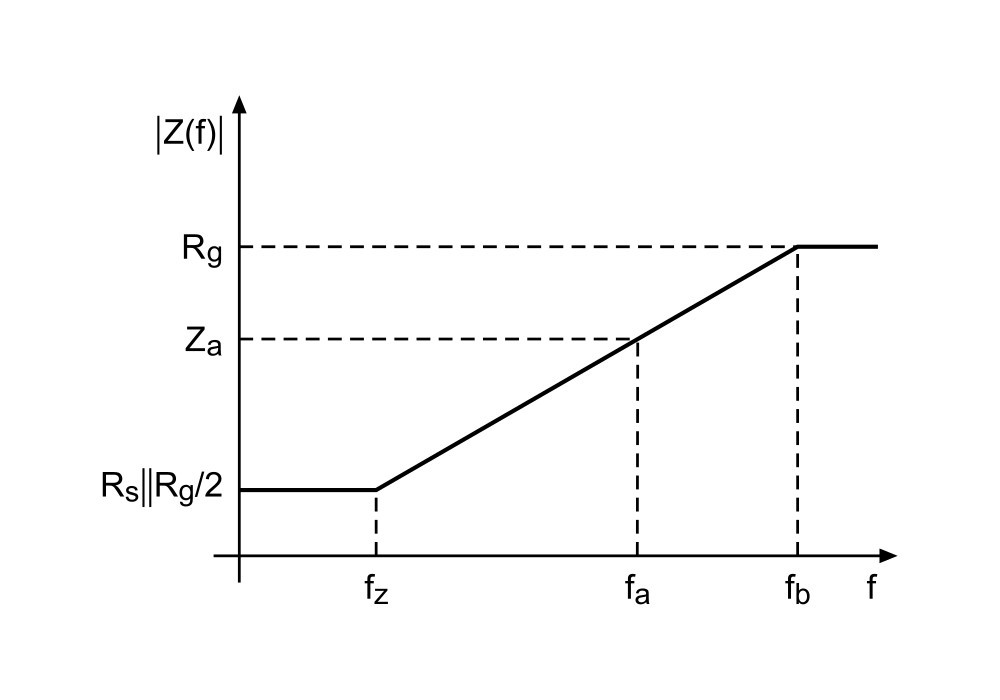
Wykres zmian modułu impedancji w funkcji częstotliwości (pulsacji) przedstawiono na rysunku 4. Charakterystyczne są dwa załamania tego wykresu odpowiadające częstotliwościom zera (fz) i bieguna (fb). W praktyce rezystancja generatora jest zwykle dużo większa od rezystancji rezystora czujnikowego. Impedancję można w takim przypadku wyrazić jako:
Jak widać, dla stanu quasi statycznego (nieco powyżej 0 Hz) oraz dla niskich częstotliwości impedancja ma wartość bliską rezystancji rezystora czujnikowego. Przy zwiększaniu częstotliwości generatora impedancja rośnie. Na wykresie z rysunku 4 można wyróżnić jeszcze jedną częstotliwość (fa), która odpowiada wzrostowi impedancji do wartości a-krotnej rezystancji rezystora czujnikowego Za=aRs. Wyrażenie (5) można przekształcić do postaci umożliwiającej obliczenie indukcyjności, dla której zachodzi powyższa sytuacja:
Przyjęcie współczynnika a takiego, by był dużo większy od 1. pozwala odsunąć się od nieliniowego odcinka charakterystyki częstotliwościowej, która występuje w pobliżu częstotliwości fz. Duży współczynnik a wymaga jednak użycia sygnału pomiarowego o dość dużej częstotliwości. Dla realnych indukcyjności rzędu setek nanohenrów pomiary musiałyby być prowadzone z częstotliwościami dochodzącymi do setek megaherców. Przyjmijmy więc a=3, dla której Za=3Rs. Wyrażenie (6) przybiera postać:
Ograniczenia metody
Niestety, opisana metoda ma pewne ograniczenia. Są to:
1. Wzrost oporu rezystora czujnikowego wraz ze wzrostem częstotliwości wynikający z efektu naskórkowości. Rezystancja zwiększa się powyżej częstotliwości, przy której zmniejsza się efektywna głębokość wnikania prądu w materiał przewodzący.
Należy zauważyć, że w rezystorach cienkowarstwowych efekt naskórkowości uwidacznia się przy wyższych częstotliwościach niż w rezystorach masowych.
2. Konieczność zamykania kabla pomiarowego terminatorem 50-omowym. Jeśli się tego nie zrobi, mogą pojawiać się odbicia sygnału powodujące powstawanie fal stojących w kablu, które będą pogarszały dokładność pomiaru. Do pomiaru nie jest więc zalecane używanie typowych sond oscyloskopowych ×10. Dobrym rozwiązaniem jest dołączenie rezystora czujnikowego bezpośrednio do gniazda generatora i dołączenie oscyloskopu kablem z terminatorem 50 W.
3. "Sondę" oscyloskopu powinien tworzyć kabel koncentryczny 50 W zakończony terminatorem 50 W, tak jak jest to widoczne w kanale 1 na fotografii 5. Takie połączenie, jak w kanale 2 na tej fotografii, jest niewłaściwe. Koniec kabla wychodzącego z generatora musi być zakończony rezystorem 50 W, który powinien być umieszczony na wejściu oscyloskopu. Daje to równoważną rezystancję źródła wynoszącą 25 W, ale nadal jest to 1000 razy więcej niż rezystora czujnikowego 25 mW.
Mimo opisanych wyżej zabiegów metoda odpowiedzi częstotliwościowej ma ograniczone zastosowanie. Obliczona na podstawie wyrażenia (7) indukcyjność Ls jest zależna od rezystancji RS, która wzrasta wraz z częstotliwością. W przypadku drutu 18 AWG (0,8 mm²) rezystancja dla wysokich częstotliwości jest już kilkakrotnie wyższa niż dla częstotliwości poniżej 100 kHz. Nieco lepiej jest w przypadku coraz bardziej powszechnych rezystorów cienkowarstwowych, ale nadal nie można pominąć wpływu zmian rezystancji Rs, gdyż przy dużych częstotliwościach nie jest do pominięcia.
Pomiar testowy z manganinowym rezystorem czujnikowym o oporności 25 mW (rys. 6) wykazał trzykrotny wzrost amplitudy przy częstotliwości 550 kHz. Obliczona z zależności (7) indukcyjność wynosi ok. 15 nH i wydaje się, że jest wiarygodna, przy czym na podstawie szacunków wynikających z geometrii można się było spodziewać indukcyjności ok. 20 mH.
Pomiar indukcyjności pasożytniczej metodą odpowiedzi impulsowej
Znacznie lepszą metodą pomiaru indukcyjności pasożytniczej rezystorów czujnikowych jest metoda odpowiedzi impulsowej. Jak wynika z nazwy, pomiar wymaga użycia generatora impulsowego. Jest to metoda oparta na dziedzinie czasu, a nie częstotliwości jak poprzednia, dzięki czemu można wyeliminować wpływ rezystancji Rs.
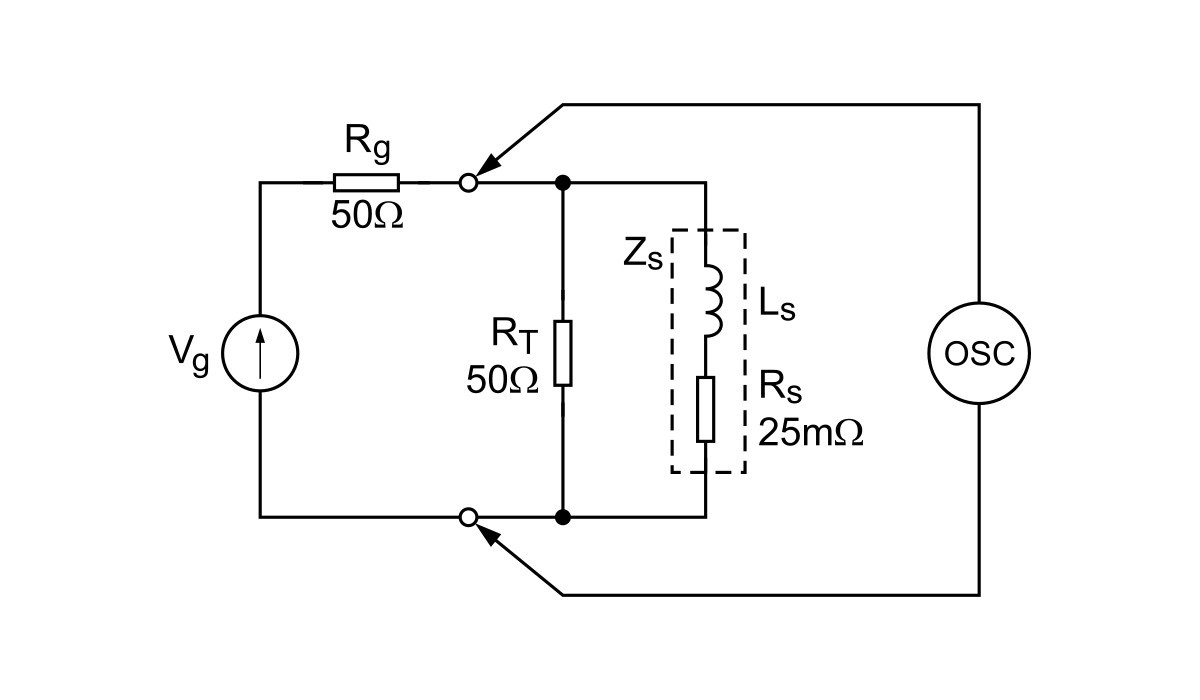
Konfiguracja pomiarowa jest taka sama, jak w poprzedniej metodzie, przy czym generator sinusoidalny został zastąpiony generatorem impulsowym. Narastające zbocze impulsu wytwarzanego przez generator osiąga 10 V w czasie 50 ns, ale amplituda impulsów jest równa 12,5 V. Szybkość narastania jest więc równa 200 V/ma. Przy zachowaniu warunku, że rezystancja wyjściowa generatora jest znacznie większa od rezystancji rezystora czujnikowego, można uznać, że mamy do czynienia ze źródłem prądowym, dla którego szybkość narastania impulsu jest równa:
Można przyjąć, że wyjściowa rezystancja generatora 50 W jest połączona szeregowo z dwiema opornościami: rezystancją terminatora 50 W dołączonego do wejścia oscyloskopu oraz równoległą do niej, wielokrotnie mniejszą impedancją Zs, która reprezentuje zastępczy schemat rezystora czujnikowego (rys. 6). Oporność terminatora może być więc w przybliżeniu traktowana jako obwód otwarty. Indukcyjność jest obliczana z zależności między napięciem i prądem:
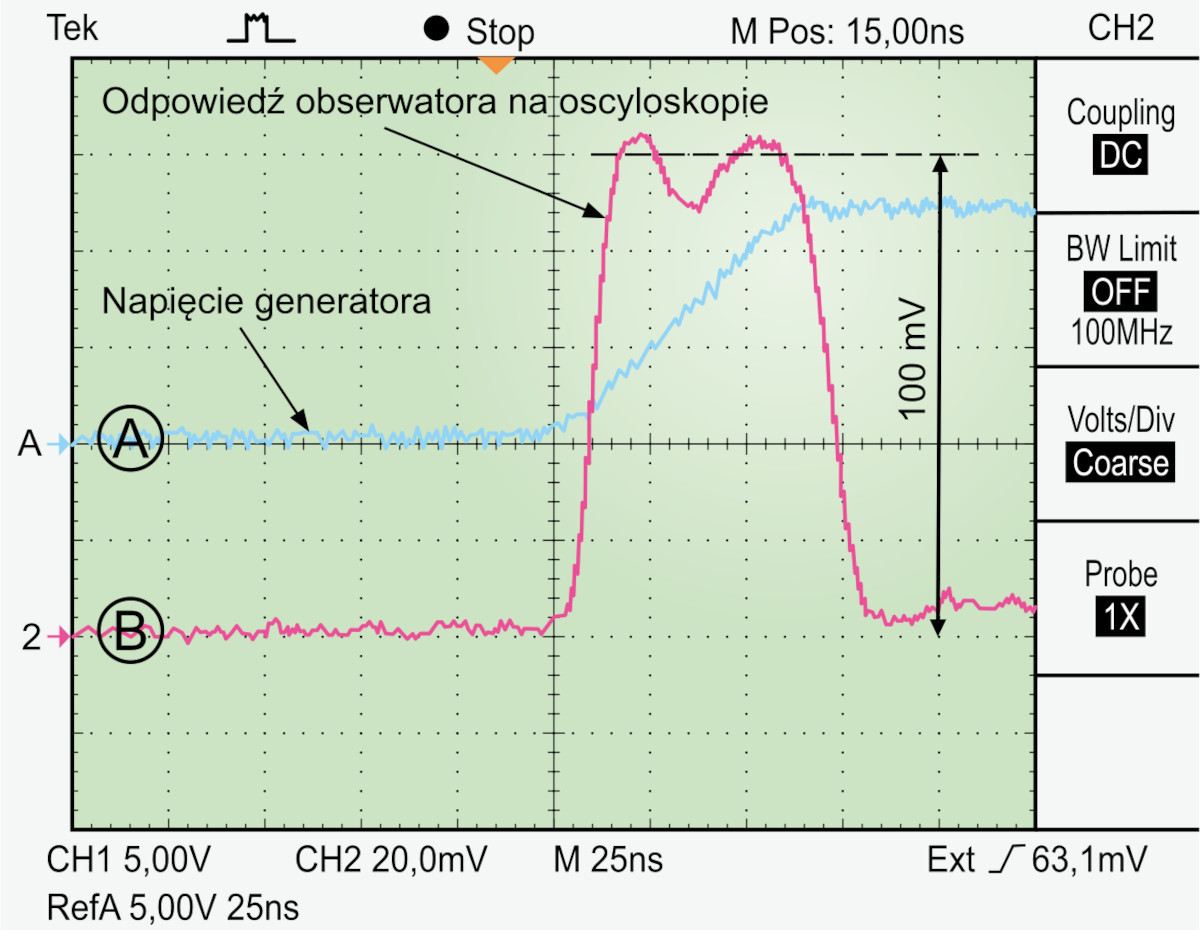
gdzie uL jest napięciem na indukcyjności, do której jest doprowadzony impuls prądowy o określonej szybkości narastania zbocza. W przedstawionym niżej przykładzie źródłem impulsu jest generator impulsowy Tektronix PG508. Przebiegi obserwowane na oscyloskopie zostały przedstawione na fotografii 7. Przebieg A generowany przez generator został zarejestrowany i zapisany jako referencyjny przy odłączonym układzie mierzonym. Następnie sygnał z generatora został doprowadzony do układu mierzonego (terminatora, rezystora czujnikowego i oscyloskopu) i dokonano obserwacji odpowiedzi (przebieg B). Należy zauważyć, że parametr określający tłumienie sondy dla wejścia kanału 2, którym obserwowano odpowiedź układu, jest ustawiony na ×1. Jest tak, ponieważ sonda de facto nie była używana, a zamiast niej zastosowano kabel zaterminowany rezystorem 50 W.
Jak widać na oscylogramie, napięcie na indukcyjności ustaliło się na poziomie ok. 100 mV. Znając określoną wcześniej szybkość narastania impulsu prądowego i napięcie w stanie statycznym na cewce, można obliczyć jej indukcyjność:
Jest to wartość wyższa niż ta, która była zmierzona metodą przemiatania częstotliwości, ale wydaje się bardziej zbliżona do szacowań opartych na podstawie geometrii badanego rezystora czujnikowego. Zmieniający się prąd wywołuje wprawdzie jednoczesne zmiany napięcia na rezystancji RS i na indukcyjności, ale zmiany uL na indukcyjności są znacznie większe niż zmiany na rezystancji, dlatego te drugie można zaniedbać. Na oscylogramie dostrzegamy ponadto nieznaczny sześcio- miliwoltowy wzrost napięcia po zakończeniu narastania impulsu prądowego. To resztkowe napięcie wynika z istnienia dzielnika utworzonego przez równolegle połączone rezystory RS i RT oraz rezystancję wewnętrzną generatora (rys. 6‒7).
Obie przedstawione metody nie dają wyników pozbawionych pewnych błędów. Mimo to, pozwalają choćby oszacować z zadawalającą dokładnością indukcyjność pasożytniczą rezystorów czujnikowych. Pomiar tego parametru mostkiem RLC również nie dałby wiarygodnego wyniku, a sięganie np. po analizatory widma wiązałoby się z dużymi kosztami stanowiska pomiarowego.
Jarosław Doliński
Źródło: Dennis Feucht, 2020 How2Power. "How To Make Sense Of Sense Resistors"
