Jitter i interferencje - dystrybucja sygnału zegarowego

Optymalizacja nadajnika

Rys. 3. Okno kalkulatora linii transmisyjnych "transcalc" z programu Qucs

Jak widać, po stronie nadajnika sygnału możliwe jest zastosowanie tylko jednej opcji. Wartość rezystora szeregowego powinna być tak dobrana, aby suma jego wartości i wyjściowej rezystancji nadajnika była równa impedancji charakterystycznej linii (Z_O). W praktyce wartość około 30Ω jest dobrym punktem startowym do dokładniejszej optymalizacji.

Metodę tę można stosować tylko wtedy, gdy impedancja wyjściowa nadajnika jest mniejsza od impedancji linii. Na szczęście większość spotykanych nadajników zbudowana jest w oparciu o układ push-pull z parą przeciwsobną na wyjściu, tak więc charakteryzuje się małą impedancją wyjściową.

Zastosowanie szeregowego rezystora nie powoduje żadnego dodatkowego statycznego przepływu prądu, ale niestety wydłuża czas narastania i opadania sygnału, zwiększając podatność systemu na jitter. Dodatkowo, należy zwrócić uwagę na maksymalną obciążalność nadajnika.

Optymalizacja odbiornika

Zastosowanie rezystora połączonego równolegle do wejścia odbiornika jest najprostszym rozwiązaniem, które można zastosować po tej stronie linii. Niestety, charakteryzuje się najgorszą efektywnością. Traconą energię można zmniejszyć, stosując dwa rezystory połączone szeregowo pomiędzy napięciem zasilania i masą, jednak kosztem zwiększenia liczby elementów.

Z tych powodów najczęściej spotykanym układem dopasowującym po stronie odbiornika jest szeregowe połączenie rezystora i kondensatora. Ten układ w ogóle nie zużywa prądu stałego. Niestety, dodany kondensator wydłuża czas propagacji sygnału przez linię.

Ponieważ stopnie wejściowe odbiornika charakteryzują się z reguły upływem, wartość rezystora dobiera się większą niż impedancja charakterystyczna linii transmisyjnej. Reasumując, w celu redukcji oscylacji należy równocześnie zastosować rezystor szeregowy po stronie nadajnika oraz szeregowe połączenie rezystora i kondensatora po stronie nadajnika. Przy wyznaczeniu wartości tych elementów pomocne są poniższe wzory:

R_s=|Z₀|-|Z_s|, zwykle |Z₀|>|Z_s|

R_L=|Z₀|

|j⋅2⋅π⋅f_tr⋅C_L|>>|Z₀^-1|

C_L~10⋅[1/(j⋅2⋅π⋅f_tr⋅|Z₀|)]=5⋅t_fr/|Z₀|

Chociaż układy dopasowujące w odbiorniku w postaci szeregowego połączenia kondensatora i rezystora mają najwięcej zalet, w specyficznym zastosowaniu prostsze metody lub ich kombinacje mogą być z powodzeniem użyte. Najlepszym kryterium weryfikacyjnym jest w takich sytuacjach eksperyment.

Niezależnie od zastosowanego układu dopasowującego potrzebna jest wiedza lub przybliżone oszacowanie impedancji nadajnika, odbiornika oraz linii transmisyjnej. Parametry układów czynnych można nawet zmierzyć, ale konstruktor nie ma na nie praktycznie wpływu. Inaczej jest z linią transmisyjną, która daje projektantowi dodatkowy stopień swobody przy konstrukcji urządzenia.

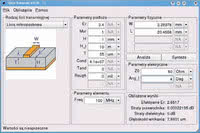
Parametry linii transmisyjnych można obliczyć przybliżonymi wzorami, jednak najlepiej posłużyć się w tym celu specjalnym oprogramowaniem. Istnieje sporo dobrych programów wspomagających projektowanie, dostępnych również w wersjach opartych na licencji GPL. Jednym z przykładów może tu być program Qucs (qucs.sf.net).

Rys. 4. Model skupiony elementu dz sprzężenia pomiędzy dwoma bezstratnymi przewodnikami

Okna kalkulatora linii transmisyjnych tego programu (w tym przypadku linii mikropaskowej) pokazano na rysunku 3. Linia mikropaskowa zbudowana jest z paska przewodnika umieszczonego nad płaszczyzną masy, pomiędzy którymi znajduje się warstwa dielektryka. Ten typ linii może być z powodzeniem stosowany na dwuwarstwowych płytkach drukowanych. Najistotniejsze parametry fizyczne tej linii to: szerokość paska W, grubość dielektryka H, względna przenikalność elektryczna dielektryka ε_r, długość paska (tym samym długość linii) L oraz grubość paska T.

W praktyce dolna warstwa metalu nie musi być płaszczyzną. Wystarczy, gdy jest szersza od górnego paska przewodnika o co najmniej 10 grubości dielektryka. Ważne jest również, aby żadne inne ścieżki oraz elementy nie znajdowały się bliżej niż 3 szerokości paska z każdej jego strony. Dostępne kalkulatory linii transmisyjnych pozwalają zarówno na syntezę, jak i analizę linii. Poprzez syntezę rozumie się wyliczenie parametrów fizycznych linii z założonych parametrów elektrycznych (impedancja, długość elektryczna).

Z kolei analiza to proces odwrotny: wyznaczenie parametrów elektrycznych z założonych parametrów fizycznych. Obie funkcje są bardzo przydatne, gdyż pozwalają zoptymalizować wybór linii. Generalnie, przy stałej grubości dielektryka szersza linia (parametr W) charakteryzuje się mniejszą impedancją. Z kolei przy tej samej szerokości W cieńszy dielektryk H to większa impedancja. Impedancja zwiększa się również, gdy przy tych samych W i H zmniejszy się przenikalność elektryczna.

Fizyczna długość paska nie ma praktycznie wpływu na impedancję charakterystyczną linii. Ma jednak znaczenie dla częstotliwości oscylacji. Przy bardzo krótkich liniach (w sensie elektrycznym) nawet przy silnym niedopasowaniu zjawisko dzwonienia może nie wystąpić. Rozróżnienie pomiędzy długością fizyczną i elektryczną wynika z częstotliwości sygnału i przenikalności elektrycznej podłoża.

Przykładowo, fizyczne 10cm linii mikropaskowej pracującej na częstotliwości 100 MHz jest elektrycznie równe 3,33cm linii pracującej na częstotliwości 300 MHz (wnosi takie samo opóźnienie fazowe). Z reguły nie można tak poprowadzić ścieżek sygnałowych, aby były tylko i wyłącznie liniami prostymi.

Występujące załamania linii mogą być dodatkowym źródłem odbić, gdyż każde z nich stanowi dodatkową pasożytniczą pojemność wpływającą na impedancję charakterystyczną linii. Aby ich uniknąć, należy załamywać linie pod maksymalnym kątem 45 stopni, a najlepiej wszelkie załamania zaokrąglać.