Wektorowe sterowanie silnikami indukcyjnymi

Podstawy

Wobec powszechnej dostępności sieci energetycznej najpopularniejsze na rynku są trójfazowe silniki indukcyjne zmiennoprądowe. Są one projektowane dla znormalizowanego napięcia i częstotliwości i zawierają trzy uzwojenia stojana zasilane napięciem trójfazowym tak nawinięte, że pod wpływem prądu zmiennego powstaje wirujące pole magnetyczne obracające wirnik.

Mimo że obroty wirnika wynikają z wirującego pola magnetycznego, w rzeczywistym układzie wirnik obraca się z szybkością mniejszą od szybkości obrotu pola magnetycznego. Różnica tych szybkości jest nazywana poślizgiem. Poślizg może być wyrażany stosunkiem częstotliwości, ale warto posługiwać się częstotliwością poślizgu.

Dla przykładowego silnika małej mocy szybkość obrotowa pola wynosi 50 obr./s, czyli 3000 obr./min., podczas gdy szybkość pod obciążeniem 2875 obr./min., czyli 47,9 obr./s. Zatem częstotliwość poślizgu wynosi 50Hz – 47,9Hz = 2,1Hz. Częstotliwość tę można przypisać źródłu zmiennoprądowemu, dostarczającemu energii do wirnika za pośrednictwem sprzężenia transformatorowego.

W wirniku jest indukowany prąd zmienny, wytwarzający w nim pole magnetyczne, dzięki czemu powstaje moment napędowy. Poślizg nadaje silnikowi zdolność do samoregulacji w pewnym stopniu swojej szybkości wirowania. Gdy wzrasta obciążenie silnika, obroty wirnika maleją. Wywołuje to wzrost częstotliwości poślizgu, zwiększający z kolei natężenie prądu i moment napędowy w wirniku.

Sterowanie szybkością

Zmiennoprądowy silnik indukcyjny może działać z różną szybkością i różnym momentem w zależności od przyłożonego napięcia zasilania i częstotliwości. Dla szybkości wirowania równej połowie szybkości nominalnej, częstotliwość wejściowa musi zostać zredukowana do połowy, czyli do 25Hz. Dla jednej czwartej szybkości nominalnej częstotliwość ta musiałaby zostać zmniejszona do 12,5Hz.

Pole magnetyczne stojana także musi być utrzymywane na stałym poziomie poprzez stałość jego prądów. Uzwojenia stojana od strony elektrycznej mają charakter indukcyjny, dlatego ze zmniejszaniem częstotliwości, przy stałym napięciu prąd stojana wzrasta. Dlatego podczas regulacji napięcie wejściowe też musi zostać obniżone, proporcjonalnie do częstotliwości.

Rys.1. Typowy profil V/Hz aplikacji sterującej silnikiem z regulowaną szybkością

Dla uzyskania działania silnika ze zmienną szybkością używa się często profilu stałego stosunku V/Hz. Stałą V/Hz dla przykładowego silnika otrzymuje się przez podzielenie napięcia pracy przez częstotliwość pracy: K = V/Hz = 230/50 = 4,6 Z zależności tej dla danej częstotliwości oblicza się wymagane napięcie: napięcie = K · częstotliwość Wynik nazywa się profilem wolto-hercowym, a jego wykres jest pokazany na rys. 1.

Nie ma ustalonej reguły opisującej proporcjonalność zależności napięcia od częstotliwości. Kształt profilu V/Hz jest często modyfikowany w celu usprawnienia działania silnika w niektórych zakresach częstotliwości. Na przykład kształt z rys. 1 został zmieniony przez podwyższenie napięcia w zakresie niskich częstotliwości. Zapewnia to zwiększenie momentu napędowego w trakcie rozruchu silnika ze stanu spoczynkowego, ułatwiające pokonanie bezwładności i tarcia początkowego.

Częstotliwość napędu może także zostać zwiększona powyżej wartości nominalnej w celu zwiększenia szybkości silnika w granicach jego mechanicznych możliwości. Jednakże w tym zakresie może wystąpić ograniczenie napięcia, a zatem i momentu napędowego silnika. Posługiwanie się do sterowania silnikiem profilem V/Hz zdaje egzamin w aplikacjach, które nie wymagają częstych zmian szybkości ani obciążenia.

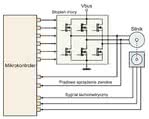
Zdarza się tak, gdy do regulowania szybkości czy prądu silnika używa się pętli sterujących. Typowy schemat blokowy systemu, nadającego się do zastosowania w profilu V/Hz, jest pokazany na rys. 2. W układzie tym użyto mikrokontrolera z wbudowanym układem PWM, sterującym sześciotranzystorowym stopniem mocy. Mikrokontroler mierzy częstotliwość, oblicza błąd szybkości i generuje sygnał sterujący, posługując się algorytmem PID.

Sygnał ten za pośrednictwem profilu V/Hz jest przekładany na wymagane napięcie i częstotliwość, a następnie kod modulujący PWM formuje sinusoidalny napięciowy przebieg sterujący o wymaganej częstotliwości i amplitudzie. Powolność metody sterowania metodą V/Hz, w przypadku aplikacji wymagających szybkiej reakcji, jest przyczyną bardzo silnego wzrostu natężenia prądu silnika w czasie zmian jego obciążenia lub szybkości wirowania.

Opóźnienia są powodowane niemożnością oddzielenia prądu sterującego momentem silnika od prądu sterującego polem w wirniku. Każda zmiana napięcia lub częstotliwości sterujących wywołuje zmiany momentu silnika i prądów w wirniku. Najlepiej byłoby, aby algorytm sterował momentem silnika niezależnie od innych jego parametrów. Wymaganie to spełnia algorytm sterowania wektorowego FOC (Field Oriented Control).

W metodzie V/Hz sterowania szybkością nie jest kontrolowana faza prądu płynącego przez uzwojenia w stosunku do napięcia, natomiast w metodzie wektorowej wraz z napięciem kontrolowane są częstotliwość poślizgu i faza dla prądu w stojanie. Metoda ta zapewnia tym samym najlepszą dla danej aplikacji sprawność i dynamikę reakcji silnika.

Sterowanie wektorowe

Rys.2. Schemat blokowy typowego systemu sterowania silnikiem z regulowaną szybkością

Wszystkie sygnały wewnętrzne silnika, widziane od strony doprowadzeń wejściowych, są sinusoidalne. Sygnały takie są trudne do przetwarzania przez program, zwłaszcza gdy do regulowania prądu są używane algorytmy PID. Jednakże po zmianie stosowanego w obliczeniach punktu odniesienia, sygnały wewnętrzne silnika zmiennoprądowego mogą być matematycznie traktowane jako wielkości stałoprądowe w stanie ustalonym.

Przy sterowaniu wektorowym w silniku zmiennoprądowym mierzone są oczywiście prądy zmienne. Niemniej w stacjonarnej płaszczyźnie odniesienia 3- fazowe zmienne prądy stojana mogą zostać zespolone w pojedynczy wirujący w czasie wektor prądowy. Zamiast odniesienia stacjonarnego można zastosować wirującą płaszczyznę odniesienia, obracającą się synchronicznie z silnikiem.

W wirującej płaszczyźnie odniesienia zmiennoprądowe wielkości w stanie ustalonym wydają się stacjonarne. Za analogię może posłużyć tor wyścigowy. Można sobie wyobrazić obserwowanie z boku kołowego toru wyścigowego. Z perspektywy stacjonarnej grupa wszystkich pojazdów porusza się wzdłuż toru z wielką szybkością, co bardzo utrudnia zorientowanie się, który z nich zdobywa przewagę.

Można również wyobrazić sobie obserwowanie wyścigu z pozycji ruchomej, podążającej za wiodącym pojazdem. Z tej perspektywy grupa pojazdów może być traktowana jako do pewnego stopnia stacjonarna. W czasie zmieniają się jedynie pozycje poszczególnych pojazdów względem lidera, który jest ruchomym punktem odniesienia. Szybkość pojazdów względem toru traci znaczenie.

Stosując tę analogię do silnika elektrycznego, szybkość pojazdów względem toru można porównać do częstotliwości, a względne wzajemne pozycje pojazdów do fazy wektora prądu w stojanie.

Transformacje układu współrzędnych

W sterowaniu wektorowym do przechodzenia ze stacjonarnej płaszczyzny odniesienia do wirującej używa się dwóch transformacji, zwanych transformacją Clarke’a i transformacją Parka. Do obliczeń koniecznie jest najpierw zmierzenie dwu z trzech prądów fazowych. Trzeci nie musi być mierzony, ponieważ suma trzech prądów fazowych jest zerowa. Zmierzone prądy przedstawiają trzy, rozmieszczone co 120º, składowe wektora prądu w trójosiowym układzie współrzędnych.

Wirujący wektor prądu łatwiej jest przedstawiać w dwuosiowym układzie współrzędnych prostokątnych, zatem transformacja Clarke’a w taki sposób przetwarza zmierzone prądy, że wektor prądu jest przedstawiany dwoma składowymi, zamiast trzema. Dwie te składowe wektorowe nadal są zmienne w czasie.

Równania transformacji Clarke’a: Iα = Ia Iβ = 0,577 (Ia + 2Ib) Następnie stosuje się transformację Parka do przejścia do 2-osiowego wirującego układu współrzędnych, współosiowego z wirującym silnikiem: Równania transformacji Parka: Id = Iα cosΘ + Iβ sinΘ Iq = –Iα cosΘ + Iβ sinΘ Kąt obrotu jest oznaczony przez Θ. Przy zastosowaniu sterowania wektorowego do 3-fazowego silnika synchronicznego wirująca płaszczyzna jest zawsze zorientowana zgodnie z jego wirnikiem, a kąt Θ otrzymuje się bezpośrednio z jego pozycji za pośrednictwem czujnika.

Jednakże omawiany silnik jest silnikiem asynchronicznym, w którego działaniu udział ma poślizg, dlatego w układach praktycznych położenie wirnika trzeba obliczyć. Jednym ze sposobów, za pomocą którego można obliczyć Θ, jest użycie równań, odzwierciedlających prądy wirnika, z których można obliczyć wymaganą częstotliwość poślizgu. Odzwierciedlenie prądów wirnika wymaga także znajomości rezystancji i indukcyjności uzwojeń wirnika.

Wielkości te definiują stałą czasową, dostosowującą poślizg silnika do poprawnej wartości w czasie nieustalonych przebiegów prądu. Po obliczeniu częstotliwości poślizgu można obliczyć Θ, korzystając z szybkości wirnika, która uwzględniając poślizg, ustawia wyprzedzenie płaszczyzny odniesienia względem wirnika. Zatem wirująca płaszczyzna odniesienia jest zgrana z zastosowanym wektorem prądowym stojana, wirującym szybciej od wirnika.

Prąd stały?

Rys.3. Przebieg zmian składowej przetransformowanego prądu stojana, przedstawiającej moment obrotowy silnika w czasie dwukrotnego wzrostu jego szybkości

Kluczem sterowania wektorowego jest to, że transformacje Clarke’a i Parka przedstawiają prądy fazowe stojana w warunkach stanu ustalonego. Ale prąd silnika jest w rzeczywistości sygnałem zmiennoprądowym, przedstawianym jako wirujący wektor prądowy, tylko dlatego, że system współrzędnych wiruje synchronicznie z wektorem prądowym, którego przetransformowane składowe prądowe są przedstawiane jako stałoprądowe. Jeśli wartość którejś ze składowych prądowych zmieni się w czasie, to znaczy, że zmieniła się amplituda lub faza wektora prądowego silnika.

Najistotniejszą cechą sterowania wektorowego jest to, że jedna składowa przetransformowanego wektora prądowego wirnika wyznacza wielkość momentu obrotowego silnika, a druga pole wirnika. Za pomocą tej metody składowa decydująca o momencie obrotowym silnika może zostać wyizolowana i kontrolowana oddzielnie. To właśnie pozwala sterować silnikiem zmiennoprądowym tak jak stałoprądowym.

Na rys. 3 pokazano przebieg w czasie przetransformowanej składowej prądowej momentu silnika kontrolowanego za pośrednictwem sterowania wektorowego w trakcie dwukrotnego przyrostu jego szybkości. Jest to sygnał "widziany" przez algorytm, a nie sygnał zmiennoprądowy, zmierzony na wyprowadzeniach silnika. Sygnał ten przedstawia prąd, potrzebny do przyspieszenia silnika do nowej szybkości.

Pętle sterujące sterowania wektorowego

W praktyce dwie przetransformowane składowe prądu są regulowane oddzielnie sterownikami PID przez program. Sygnały wyjściowe tych dwóch sterowników PID dostarczają dwóch składowych wektora napięciowego, które decydują, jak fazy silnika muszą być zasilone dla uzyskania wymaganych prądów stojana. Wejście odniesienia jednego ze sterowników PID otrzymuje wartość stałą, tak aby wirnik generował stałe pole. Wejście odniesienia drugiego sterownika PID wyznacza wielkość momentu napędowego silnika.

Poziom odniesienia momentu obrotowego jest zwykle dostarczany przez pętlę sterującą trzeciego PID, regulującą szybkość silnika. Ostatnim krokiem procesu sterowania wektorowego jest rozwinięcie składowych wektora napięciowego, które zostały wygenerowane w wirującej płaszczyźnie odniesienia. Wartość Θ, która została obliczona z równań prądu wirnika, zostaje użyta w odwrotnych transformatach Clarke’a i Parka, bardzo podobnych do pokazanych powyżej transformat pierwotnych.

Mimo że równania sterowania wektorowego nie są skomplikowane, dla uzyskania dobrych wyników muszą być rozwiązywane stosunkowo często. Wykorzystując wartość Θ z poprzedniej iteracji równań sterowania wektorowego, transformowane są zmierzone wartości prądu i obliczane nowe wartości Θ za pomocą równań określających prąd wirnika. Kolejne iteracje równań są zwykle rozwiązywane co 50µs, aby zminimalizować wielkość błędu kątowego wirnika, co w praktyce powoduje, że do sterowania wymagany jest szybki 16-bitowy mikrokontroler lub procesor sygnałowy.

Przykładową realizację algorytmu sterowania wektorowego można znaleźć w nocie aplikacyjnej AN908, dostępnym w witrynie internetowej Microchip www.microchip.com . Oprócz szczegółowego opisu dostępny jest kod źródłowy dla procesorów dsPIC.

Steve Bowling, Microchip Technology