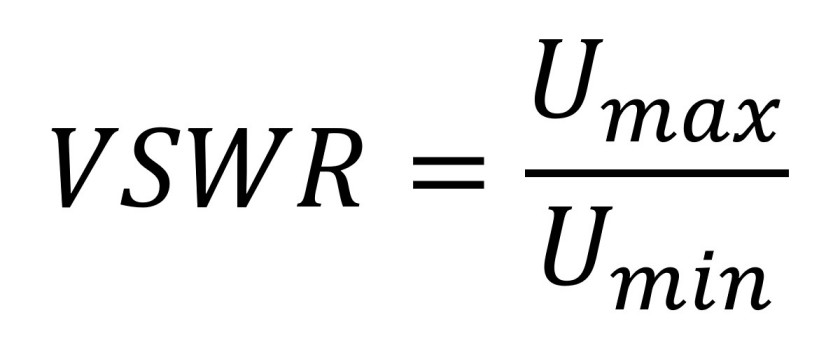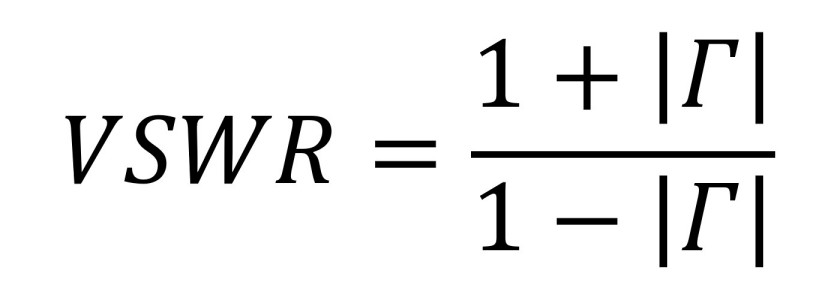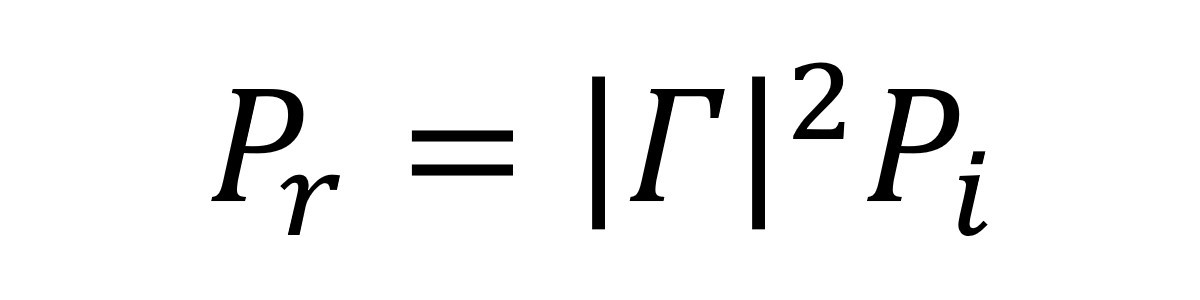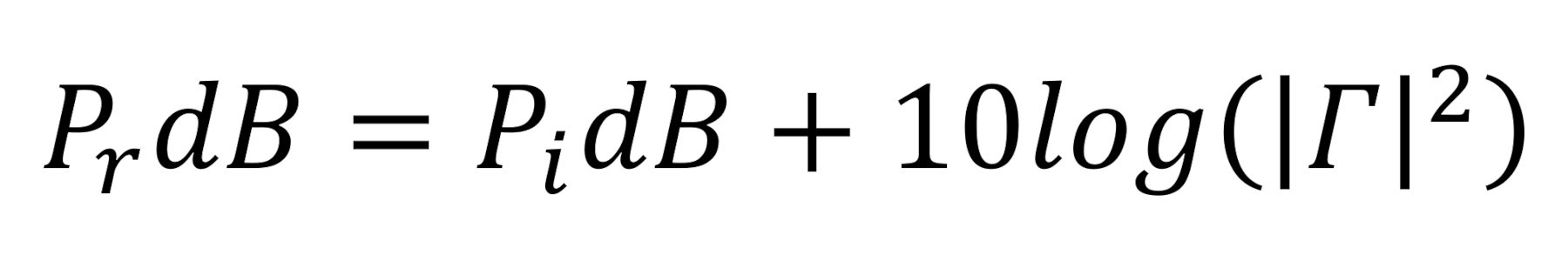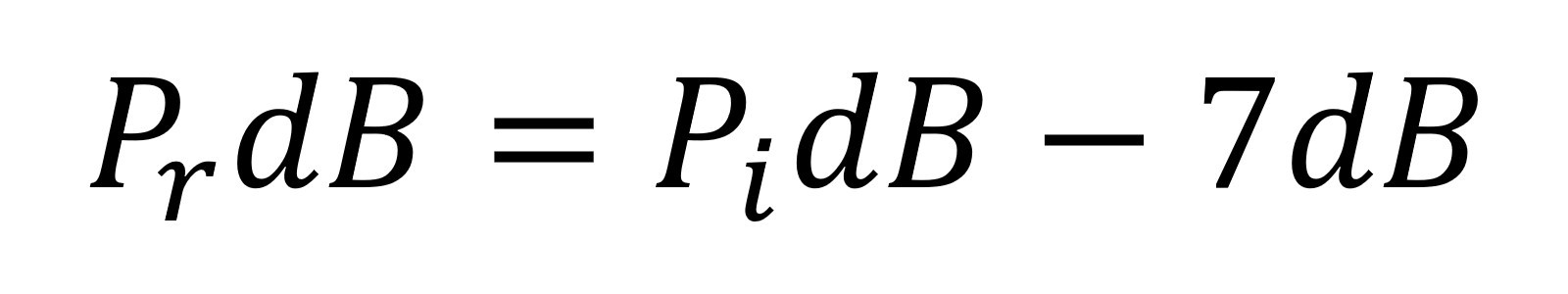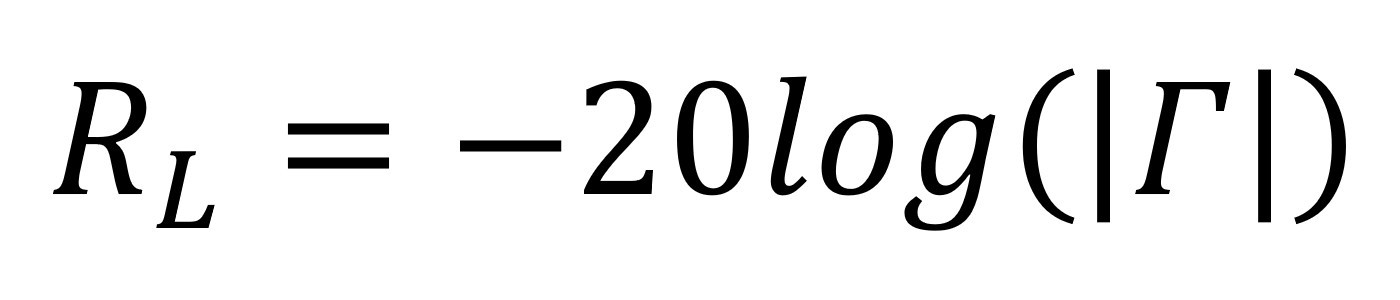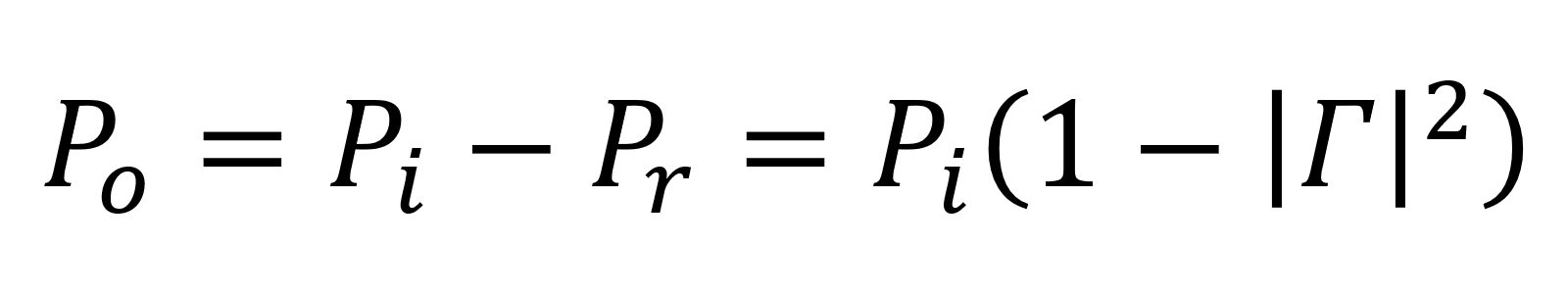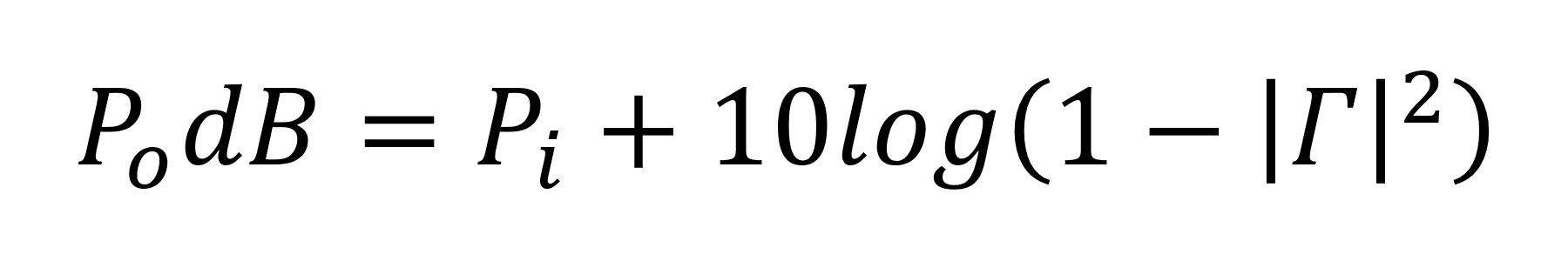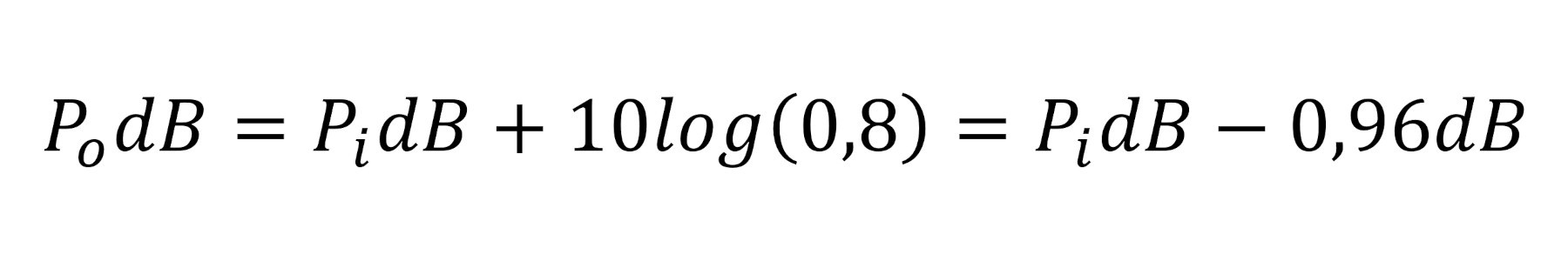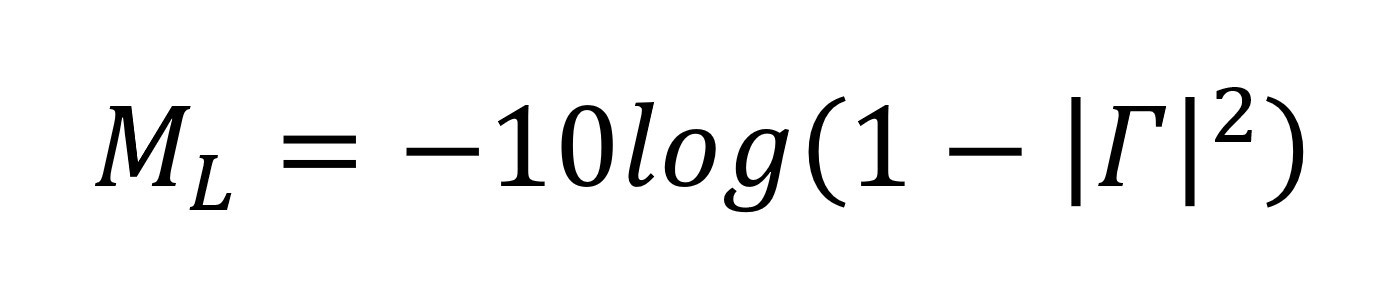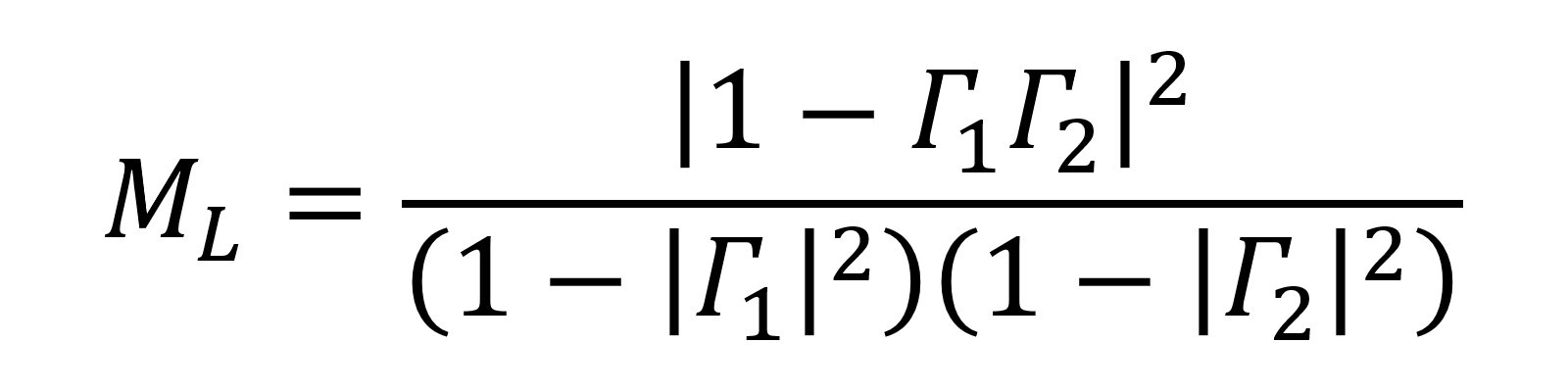Odbicia fal w liniach transmisyjnych

Fale generalnie zachowują się w sposób szczególny. Na przykład świetlne przy przejściu z jednego ośrodka, jak powietrze, do innego, jak szkło, załamują się. Zachodzi wtedy zjawisko refrakcji. Fale w wodzie, jeżeli napotkają przeszkodę, jak łódź albo skała, uginają się (dyfrakcja). Dźwiękowe z kolei nakładają się na siebie (interferencja).

Fale elektromagnetyczne podlegają zachowaniom, których przeważnie nie kojarzymy z sygnałami elektrycznymi. Ich nieznajomość nie zaskakuje, ponieważ zjawiska te w "zwykłych" obwodach są pomijalne, a ujawniają się dopiero w zakresie w.cz. dla sygnałów, które są przesyłane liniami transmisyjnymi.

Linie transmisyjne

Te ostatnie są tak klasyfikowane, jeżeli ich długość wynosi przynajmniej jedną czwartą długości fali sygnału. Przykładowo dla sygnału o częstotliwości 1 kHz, którego długość fali wynosi 300 km i sygnału o częstotliwości 1 GHz o długości fali 30 mm, graniczne długości linii transmisyjnych wynoszą odpowiednio 75 km i 7,5 mm.

Zatem w zakresie bardzo małych częstotliwości zjawiska charakterystyczne dla linii transmisyjnych są znikome. W przypadku średnich częstotliwości szczególnej uwagi wymagają tylko bardzo długie kable. Jednak przy częstotliwościach rzędu gigaherców jak linie transmisyjne trzeba traktować nawet ścieżki na płytkach drukowanych.

Konsekwencją tego jest to, że nie można już sygnału postrzegać jako jednokierunkowego, który płynie od źródła do obciążenia. Projektując obwody w.cz., trzeba mieć świadomość, że może się on przemieszczać w obu kierunkach, również – z powodu odbić – od obciążenia do źródła.

Odbicia

Odbicia występują, gdy fala napotyka nieciągłość. Dzieje się tak podczas sztormu, gdy fale morskie uderzają w skały, od których się odbijają. Inaczej jednak zachowują się te, które wpływają na plażę. Łatwo jest wyjaśnić tę różnicę.

Fale przenoszą energię. Kiedy rozprzestrzeniają się w otwartej wodzie, przepływa ona swobodnie. Gdy jednak fala napotka nieciągłość, przepływ energii zostaje przerwany – zarówno w kontakcie ze skałą, jak i po wpłynięciu na plażę dalsza propagacja fali nie jest już możliwa.

Oczywiście energia przenoszona przez fale nie może po prostu zniknąć, zostaje zatem odbita albo pochłonięta. W przypadku uderzenia w skałę to drugie nie jest możliwe, więc następuje odbicie – wówczas energia kontynuuje rozchodzenie się w postaci fali, ale w przeciwnym kierunku. Na plaży natomiast energia fali ulega stopniowemu rozproszeniu – piasek wchłania wodę, zatem odbicie jest minimalne.

Impedancja charakterystyczna

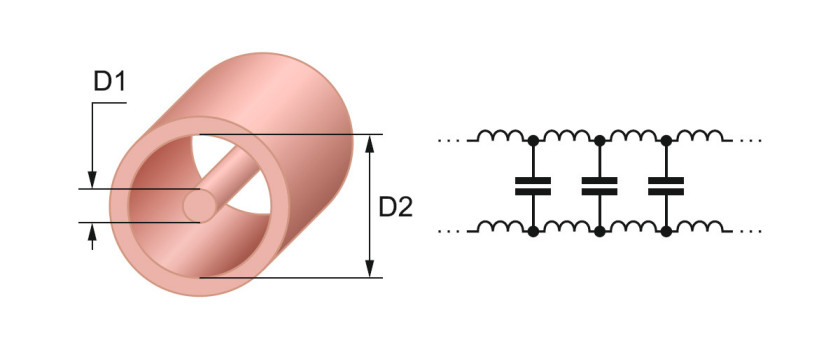
W obwodach elektrycznych także występują nieciągłości, które wpływają na propagację fal. W tym kontekście krytyczne znaczenie ma impedancja charakterystyczna. Jest to najważniejszy parametr linii transmisyjnej. Zależy od jej właściwości fizycznych. Na przykład w kablach koncentrycznych (rys. 1) jest funkcją średnicy wewnętrznej, zewnętrznej oraz względnej przenikalności elektrycznej izolacji między przewodami wewnętrznymi i zewnętrznymi.

 

Rys. 1. Kabel koncentryczny i jego schemat zastępczy uwzględniający rozproszoną pojemność i indukcyjność

Fala i przenoszona przez nią energia rozchodzą się w linii transmisyjnej w kierunku od źródła do obciążenia. Maksymalny transfer mocy następuje, gdy impedancja obciążenia jest równa impedancji źródła (impedancji charakterystycznej linii transmisyjnej). Przy dopasowanych impedancjach, kiedy nie występuje nieciągłość, obciążenie pochłania całą energię fali. W przeciwnym razie tylko jej część zostaje zaabsorbowana, zaś pozostała energia jest odbijana w postaci fali przemieszczającej się w przeciwnym kierunku.

Na ilość energii odbitej wpływa stopień niedopasowania impedancji źródła i obciążenia. Najgorszy przypadek zachodzi, gdy obwód jest otwarty albo zwarty, co oznacza odpowiednio nieskończoną i zerową impedancję obciążenia. Wówczas występuje całkowita nieciągłość. W rezultacie energia w ogóle nie zostaje pochłonięta i w całości ulega odbiciu.

Skutki niedopasowania

Odbicia sygnału w linii transmisyjnej mają negatywne konsekwencje. Przede wszystkim pogarszają sprawność transmisji. Jeżeli mamy wzmacniacz mocy podłączony do anteny, nie chcemy przecież, żeby połowa mocy wyjściowej została odbita z powrotem do niego, zamiast przekształcić się w użyteczne promieniowanie elektromagnetyczne. Ponieważ celem jest przeniesienie mocy ze źródła do obciążenia, odbicia muszą być ograniczone do minimum.

Druga kwestia dotyczy rozkładu fali w linii transmisyjnej. Ciągły sygnał przesyłany w warunkach niedopasowania impedancji spowoduje wystąpienie ciągłego sygnału odbitego. W rezultacie fale padająca i odbita skierowane w przeciwnych kierunkach będą się niejako mijały, nakładając się na siebie miejscami.

W wyniku interferencji powstanie fala stojąca. Spowoduje to zmiany amplitudy sygnału wzdłuż długości kabla – miejscami będzie większa, a miejscami mniejsza. Fala stojąca skutkuje zatem powstawaniem napięć większych niż napięcie przesyłanego sygnału. Miejscami może mieć to poważne konsekwencje, powodując nawet uszkodzenie linii transmisyjnej.

Współczynnik fali stojącej

Kiedy zachodzi całkowite odbicie, minimalna wartość amplitudy fali stojącej Umin wynosi 0. Przy częściowym odbiciu z kolei wartość Umin zbliża się do wartości szczytowej Umax. W idealnym przypadku, gdy nie ma odbicia, Umax staje się równe Umin. Stosunek Umax do Umin, znany jako współczynnik fali stojącej VSWR (Voltage Standing Wave Ratio), charakteryzuje odbicie występujące przy nieciągłości impedancji. Wyraża go wzór:

Gdy występuje całkowite odbicie, współczynnik fali stojącej ma wartość nieskończoną. W razie dopasowanego obciążenia VSWR jest równy 1. W pozostałych przypadkach wartość VSWR mieści się w przedziale między tymi dwoma skrajnymi wartościami. Współczynnik fali stojącej jest powiązany ze współczynnikiem odbicia Γ za pomocą następującego równania:

Straty odbiciowe

Na rysunku 2 została przedstawiona linia transmisyjna połączona z wejściem komponentu RF. Moc padająca wynosi P_i, a współczynnik odbicia od strony wejścia elementu RF wynosi Γ. Jeżeli chcemy określić, ile mocy padającej ulega odbiciu (P_r), musimy pamiętać, że o ile współczynnik odbicia Γ jest stosunkiem napięcia odbitego do napięcia padającego, o tyle IΓI² reprezentuje stosunek mocy odbitej do mocy padającej. Stąd:

Na wyrażenie powyższego równania w decybelach pozwala formuła:

Na przykład IΓI²=0,2, jeżeli, otrzymujemy zależność:

Oznacza to, że moc odbita jest o 7 dB mniejsza niż moc padająca. Można zatem powiedzieć, że część sygnału wejściowego, która uległa odbiciu, została wzmocniona o –7 dB lub, równoważnie, stłumiona o +7 dB. Innymi słowy, w tym przykładzie straty odbicia wynoszą 7 dB. W przypadku obwodów pasywnych, w których wartość współczynnika odbicia Γ mieści się między 0 a 1, odbity sygnał ulega raczej tłumieniu niż wzmocnieniu.

W zastępstwie formuł 3 i 4 wykorzystuje się straty odbiciowe R_L. Wyraża je formuła:

Na przykład, jeśli straty odbiciowe wynoszą 30 dB, oznacza to, że moc odbita jest o 30 dB mniejsza niż moc padająca. Generalnie większe straty odbiciowe odpowiadają dokładniejszemu dopasowaniu impedancji obciążenia do impedancji charakterystycznej linii.

Przedstawione parametry: współczynnik odbicia Γ, współczynnik fali stojącej VSWR oraz straty odbiciowe R_L, pozwalają na różne sposoby określić, jak dobrze obciążenie zostało dopasowane do linii transmisyjnej. Trzeba przy tym pamiętać, że w przeciwieństwie do współczynnika odbicia Γ, który niesie ze sobą informacje zarówno o wartości, jak i fazie, pozostałe dwa dostarczają jedynie informacji o wartości.

Straty niedopasowania

Oprócz mocy odbitej kluczowe jest także określenie wpływu niedopasowania impedancji na ilość mocy przekazywanej do wyjścia (P₀). Załóżmy, że wzmocnienie mocy elementu RF wynosi 1 (G=1). Oznacza to, że moc, która jest doprowadzana na wejście elementu RF, pojawia się na jego wyjściu. Ponieważ niedopasowanie impedancji skutkuje tym, że część mocy ulega odbiciu, zmniejsza moc przekazywaną do komponentu RF. Przy G=1, moc wyjściowa P₀ jest równa różnicy między mocą padającą a mocą odbitą:

Wyrażenie powyższego równania w decybelach prowadzi do zależności:

Jeżeli otrzymujemy zależność:

Oznacza to, że moc wyjściowa jest o 0,96 dB mniejsza od mocy wejściowej. Innymi słowy, sygnał zostaje wzmocniony o –0,96 dB albo, równoważnie, stłumiony o +0,96 dB. Ten spadek mocy, będący skutkiem niedopasowania impedancji, nazywany jest stratą niedopasowania. Określa on w praktyce, jak dużą poprawę wzmocnienia możemy uzyskać, jeżeli zapewnimy idealne dopasowanie impedancji. W powyższym przykładzie wynosi ona 0,96 dB. Podsumowując, straty z powodu niedopasowania (ML) wyraża się następującym równaniem:

Dwustronne niedopasowanie

W przykładzie z rysunku 2 założyliśmy, że impedancja źródła sygnału jest dopasowana do impedancji charakterystycznej linii transmisyjnej. Jeśli jednak tak nie jest, moc P_r ponownie odbije się od nieciągłości od strony źródła sygnału. To będzie skutkować powstaniem fali padającej P_i.

 

Rys. 3. Dwustronne niedopasowanie

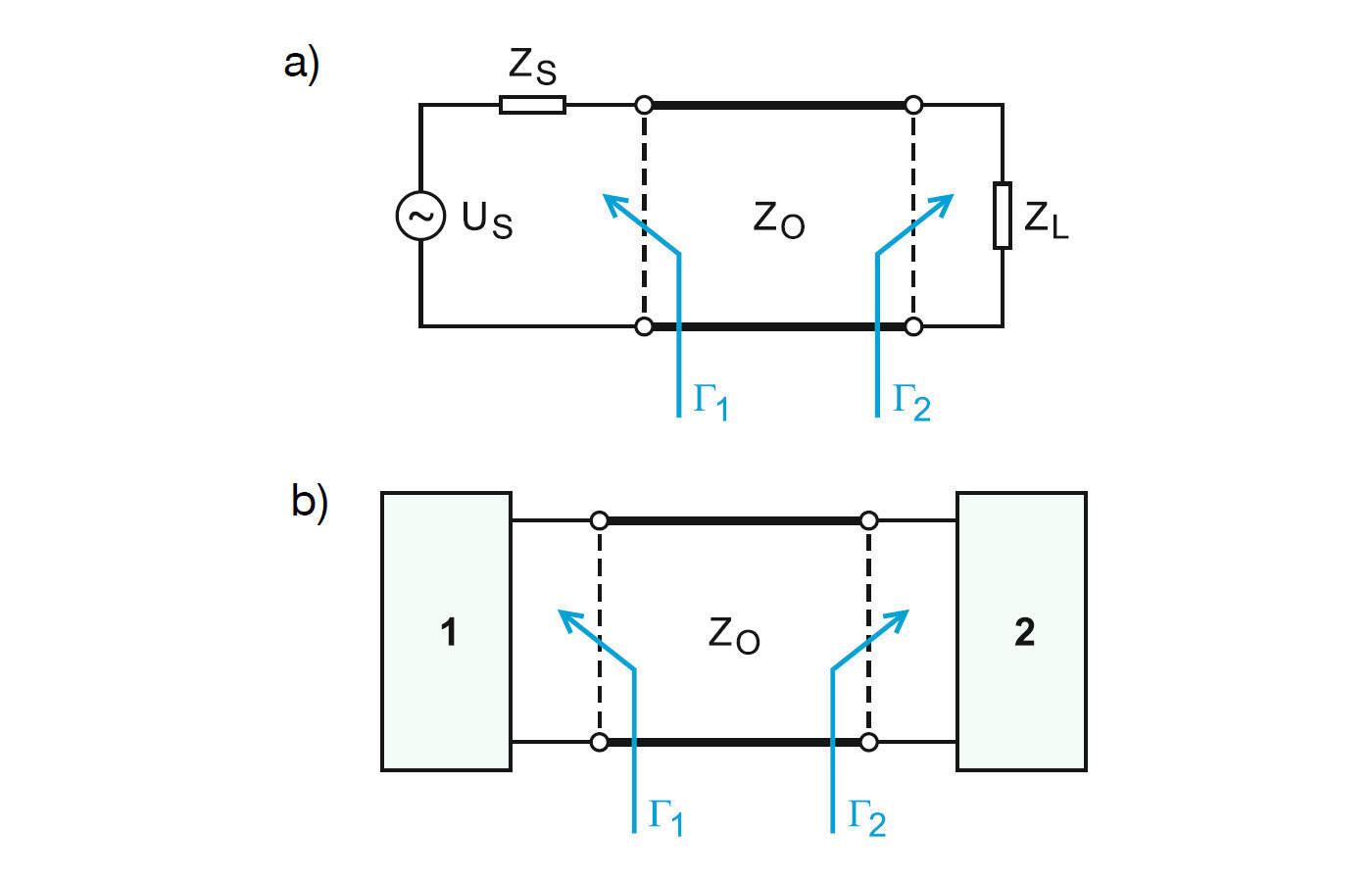
Z taką sytuacją mamy do czynienia na przykład wtedy, gdy podłączymy źródło do obciążenia przez linię transmisyjną (rys. 3 a) lub na styku dwóch urządzeń połączonych kaskadowo (rys. 3 b). W takim przypadku strata z powodu niedopasowania (niewyrażana w decybelach) jest określona równaniem:

Powyższe równanie określa część mocy wejściowej, która odbija się tam i z powrotem między portami wejściowym i wyjściowym z powodu zjawiska odbicia fal.

Załóżmy, że Γ₁ i Γ₂ wynoszą odpowiednio 0,4 i 0,5. W tym przypadku mamy stratę z powodu niedopasowania M_L równą 1,02. Wyrażona w dB wynosi 0,09 dB. Należy jednak pamiętać, że współczynnik Γ niesie ze sobą informacje zarówno o wielkości, jak i fazie, zaś kąt fazowy może wpływać na wartość M_L obliczaną według równania 11. Stąd na przykład, jeżeli Γ₁=0,4 i Γ₂=–0,5 M_L, wyniesie 2,3 lub 3,6 dB.

Ponieważ straty niedopasowania zależą od kąta fazowego współczynników odbicia i biorąc pod uwagę, że przeważnie w praktyce znana jest jedynie wartość współczynnika odbicia, trudno jest precyzyjnie wyznaczyć, ile mocy jest faktycznie przenoszone z wejścia na wyjście. Dlatego na przykład, jeżeli IΓ₁I=0,4 i IΓ₂I=0,5, strata niedopasowania mieścić się będzie w przedziale od 0,09 dB do 3,6 dB.

Monika Jaworowska