Przy wyższych częstotliwościach, gdy długość połączeń jest porównywalna z długością fali, sygnał należy opisywać jako falę przemieszczającą się wzdłuż przewodu. Jego wielkość jest wtedy funkcją czasu i położenia. Uniemożliwia to bezpośrednie stosowanie praw mających zastosowanie do "zwykłych" obwodów elektrycznych. Dla odróżnienia złożonego sposobu propagacji sygnałów w zakresie w.cz. wprowadza się także termin linii transmisyjnej.
Linię transmisyjną modeluje się, dzieląc ją na wiele elementów o nieskończenie małej długości. Każdy z nich przedstawia się na schemacie zastępczym jako połączenie elementów RLC, jak na rys. 1a. R i G reprezentują w tym obwodzie odpowiednio rezystancję jednostkową przewodnika oraz przewodność jednostkową dielektryka między przewodami. L i C to natomiast indukcyjność oraz pojemność na jednostkę długości linii transmisyjnej.
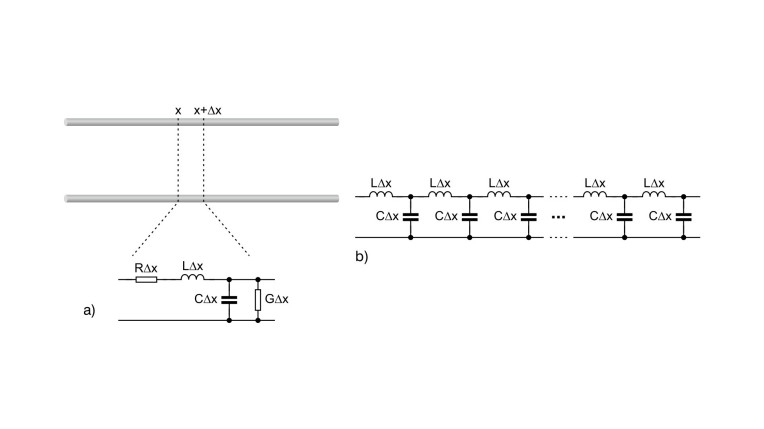
Przy częstotliwościach radiowych reaktancja szeregowa (cewki) jest typowo znacznie większa niż rezystancja szeregowa, a reaktancja równoległa (kondensatora) jest przeważnie znacznie mniejsza od rezystancji w równoległej gałęzi obwodu. Można więc obydwie rezystancje pominąć. Bezstratną linię transmisyjną, bez elementów R i G, można zamodelować obwodem zastępczym jak na rysunku 1b. W wielu zastosowaniach straty w liniach transmisyjnych należy jednak uwzględnić.
Skutki tłumienia
Podczas przemieszczania się wzdłuż linii stratnej sygnał ulega bowiem osłabieniu. Tłumienie rośnie liniowo wraz z odległością. Na przykład jeżeli jest równe 0,1 dB/m, na końcu odcinka o długości 5 metrów wyniesie 0,5 dB. W miarę oddalania się od źródła sygnału jego amplituda zmniejsza się z kolei wykładniczo. Oprócz tego straty w linii transmisyjnej zwiększają się wraz z częstotliwością – ma ona dolnoprzepustową charakterystykę tłumienia.
Ma to znaczenie zwłaszcza w transmisji sygnałów cyfrowych. W ich widmie przejściom pomiędzy poziomami logicznymi w dziedzinie czasu odpowiadać będą składowe wysokiej częstotliwości. Na przykład w widmie idealnego przebiegu prostokątnego o współczynniku wypełnienia 50% oraz zerowych czasach narastania/opadania wystąpią wszystkie nieparzyste harmoniczne częstotliwości podstawowej.
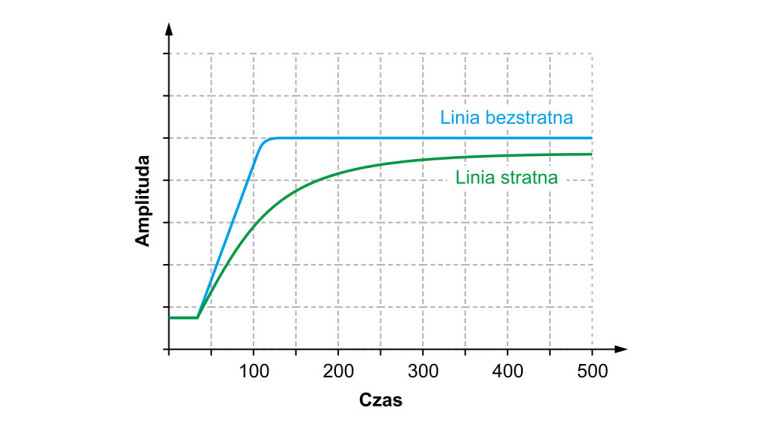
Kiedy taka fala prostokątna o nieskończenie szerokim paśmie będzie się rozprzestrzeniać wzdłuż stratnej linii transmisyjnej, jej składowe wysokoczęstotliwościowe będą silnie tłumione. To będzie powodowało zniekształcenia sygnału poprzez wzrost czasów narastania/opadania. Dodatkowo na skutek tłumienia będzie również malała amplituda, co jednak w przypadku sygnałów cyfrowych ma mniejsze znaczenie niż wydłużenie czasu narastania/opadania impulsu (rys. 2). To bowiem skutkuje wystąpieniem interferencji międzysymbolowych w strumieniach transmitowanych bitów, co z kolei ogranicza prędkość przesyłu danych i pogarsza jakość transmisji.
Straty w linii transmisyjnej stanowią sumę strat dielektrycznych i strat w przewodniku. Te pierwsze odpowiadają części energii rozpraszanej na ciepło w dielektryku po przyłożeniu pola elektrycznego. Straty dielektryczne zależą od właściwości dielektryka – na ich ilość wpływają wartości tangensa kąta stratności i względnej przenikalności elektrycznej (stałej dielektrycznej). Zwykle wzrastają w wyższych częstotliwościach i im większą wartość mają tangens kąta stratności oraz względna przenikalność elektryczna.

Straty dielektryczne
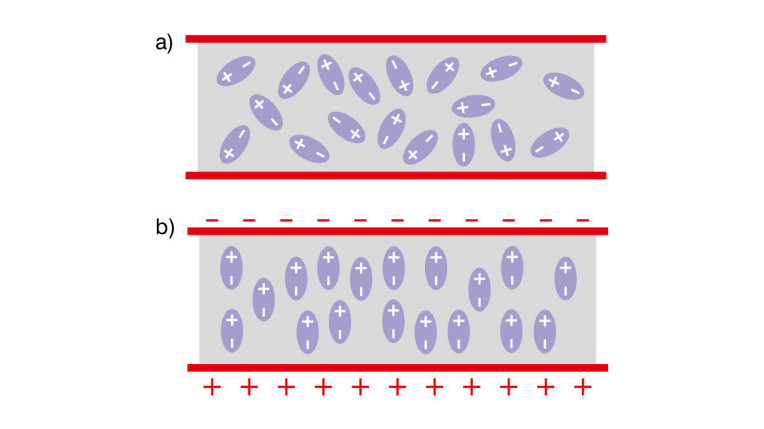
Na rysunku 3a przedstawiono dielektryk zbudowany z cząsteczek polarnych (dipoli). W przypadku braku zewnętrznego pola elektrycznego są one zorientowane losowo. Po jego przyłożeniu następuje ich polaryzacja – ładunki przemieszczają się względem zewnętrznego pola elektrycznego, jak na rys. 3b. Prowadzi to do zaindukowania ładunku powierzchniowego o przeciwnej polaryzacji na przeciwległych powierzchniach dielektryka.
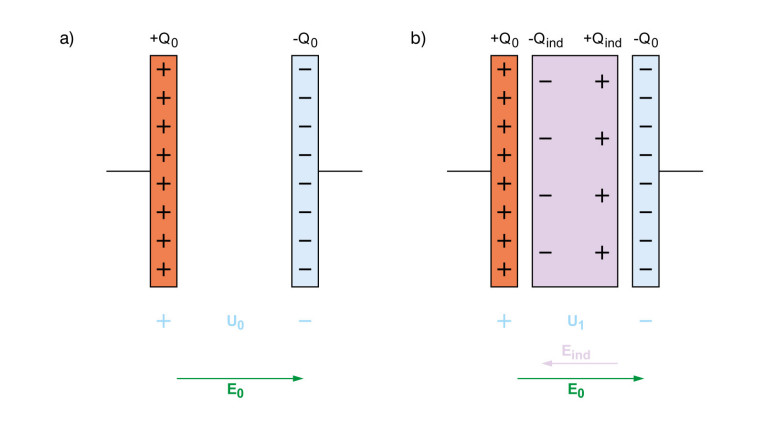
Na rysunku 4a przedstawiono naładowany kondensator o napięciu U0 i ładunku Q0 na każdej z jego płytek. Pole elektryczne pomiędzy nimi wynosi E0. Zakładamy, że kondensator jest odłączony od źródła napięcia i nie ma drogi jego rozładowania. Jeśli umieścimy dielektryk między jego płytkami, jak pokazano na rysunku 4b, zgodnie z tym co pisaliśmy wyżej, dipole elektryczne dielektryka ustawią się zgodnie z polem zewnętrznym, a na jego przeciwległych powierzchniach pojawi się ładunek Qind, ujemny, zwrócony w stronę dodatnio naładowanej płytki kondensatora i dodatni w pobliżu płytki naładowanej ujemnie. Zaindukowane ładunki wytworzą wewnętrzne pole elektryczne, które będzie skierowane przeciwnie do zewnętrznego pola elektrycznego między płytkami kondensatora. W rezultacie całkowite pole elektryczne, równe E0 − Eind, i napięcie między płytkami kondensatora zmniejszą się (U1 < U0). Ponieważ ładunek zgromadzony na płytkach kondensatora jest taki sam, podczas gdy napięcie na kondensatorze jest mniejsze, odpowiada to wzrostowi pojemności.
Kąt stratności. Stała dielektryczna
W dielektrykach z niepolarnymi cząsteczkami także zachodzi opisane zjawisko. W takim przypadku zewnętrzne pole elektryczne powoduje rozdzielenie ładunku i indukowanie dipoli. Te ustawiają się następnie w kierunku linii pola zewnętrznego tak jak dipole cząsteczek polarnych.
Generalnie, jeżeli ruch dipoli skutkuje pojawieniem się składowej prądu, która wyprzedza napięcie kondensatora o dokładnie 90°, dielektryk zwiększa jego pojemność. Przemieszczenia dipoli, które prowadzą do wystąpienia prądu w fazie z napięciem kondensatora, są modelowane przez składową rezystancyjną. Są one przyczyną strat przedstawianych jako element G na schemacie zastępczym linii transmisyjnej. Charakteryzuje je tangens kąta δ odchylenia kątowego od 90° (tg δ, tangens kąta stratności).

Względna przenikalność elektryczna natomiast, w uproszczeniu, charakteryzuje to, jak dobrze dany materiał dielektryczny "utrzymuje" pole elektryczne. Definiuje się ją jako stosunek pojemności kondensatora z danym dielektrykiem do pojemności kondensatora z próżnią zamiast niego. Stała dielektryczna większości materiałów używanych do budowy PCB mieści się w zakresie od 2,5 do 4,5, chociaż w przypadku niektórych materiałów ceramicznych, takich jak m.in. tytanian baru, sięga nawet 7000.
Stała dielektryczna bezstratnego materiału dielektrycznego jest wartością rzeczywistą, a stratnego – wartością zespoloną. Podstawiając ją we wzorze na admitancję, również uzyskujemy dwa człony. Część urojona admitancji odpowiada idealnemu bezstratnemu kondensatorowi, podczas gdy część rzeczywista odpowiada stracie dielektrycznej. Pozwala to na powiązanie tangensa kąta stratności ze względną przenikalnością elektryczną – tg δ jest definiowany jako stosunek części rzeczywistej i urojonej stałej dielektrycznej.
Straty w przewodniku
Przy prądzie stałym rezystancję jednostkową przewodnika można obliczyć jako iloraz jego rezystywności ρ (Ω·m) i pola przekroju poprzecznego A (m²):
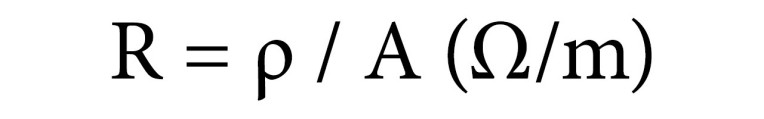
Rozkład prądu w przekroju poprzecznym przewodnika jest wtedy równomierny. Wraz ze wzrostem częstotliwości prąd ma jednak tendencję do przepływu przez płytką warstwę tuż pod powierzchnią przewodnika. Zjawisko to, znane jako efekt naskórkowości, skutkuje zmniejszeniem efektywnego przekroju poprzecznego przewodnika, a tym samym prowadzi do zwiększenia się jego rezystancji. Głębokość warstwy, przez którą przepływa większość prądu, jest wyrażana zależnością:
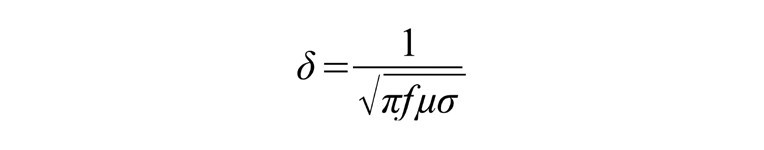
gdzie: μ to przenikalność magnetyczna przewodnika (H/m), a σ – jego przewodność w (S/m). Stąd efektywny przekrój poprzeczny przewodnika zmniejsza się wraz z pierwiastkiem kwadratowym częstotliwości, co z kolei oznacza, że rezystancja przewodnika przy wyższych częstotliwościach jest proporcjonalna do pierwiastka kwadratowego częstotliwości.
Warto w tym miejscu doprecyzować, że głębokość naskórkowości określa odległość, na której gęstość prądu zmniejsza się o współczynnik 1/e w stosunku do jego gęstości przy powierzchni przewodnika. Dlatego gęstość prądu nie spada nagle do zera poniżej δ. Dla uproszczenia zazwyczaj zakłada się jednak, że cały prąd jest równomiernie rozłożony na tej głębokości pod powierzchnią przewodnika. Przykładowo w przypadku miedzi przy częstotliwości 1 GHz wynosi ona około 2 μm. Wraz ze wzrostem częstotliwości δ maleje.
Podsumowanie
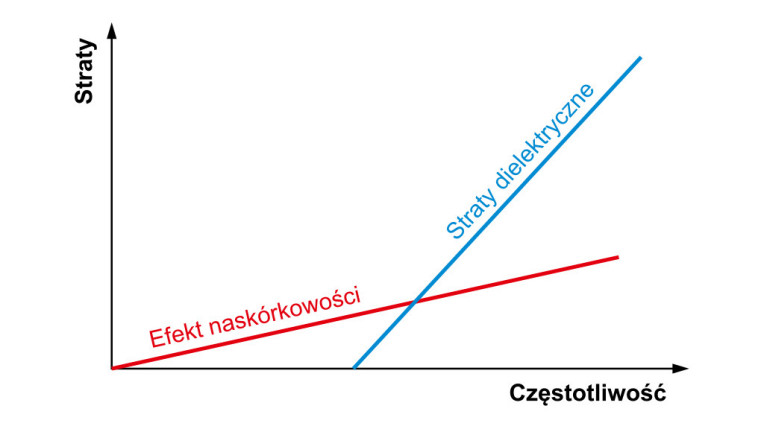
Straty w przewodniku rosną wraz z pierwiastkiem kwadratowym częstotliwości, natomiast straty dielektryczne są do niej wprost proporcjonalne. W rezultacie w zakresie niższych i średnich częstotliwości te drugie są pomijalnie małe, zaś straty w linii transmisyjnej są determinowane przez efekt naskórkowości. Przy wyższych częstotliwościach strata dielektryczna ma decydujący wpływ, ponieważ rośnie szybciej niż straty w przewodniku. Zależności te przedstawiono na rysunku 5.
Monika Jaworowska













