Punkt przechwytu trzeciego rzędu to jeden z najważniejszych parametrów charakteryzujących analogowe układy wysokiej częstotliwości

Rys. 1. Składowe szeregu Taylora w skali logarytmicznej

W przypadku wzmacniaczy, stopni przemiany, generatorów VCO, itd. dąży się do liniowego odwzorowania pewnej cechy sygnału wejściowego na inną cechę sygnału wyjściowego. Przykładowo, idealny wzmacniacz odpowiada na sygnał x(t) sygnałem y(t) spełniającym zależność y(t) = A·x(t), gdzie współczynnik A jest wzmocnieniem wzmacniacza.

Podobnie generator VCO odpowiada na sygnał x(t) sygnałem f_y(t) = A·x(t), a zatem częstotliwość wyjściowa jest proporcjonalna do wartości sygnału wejściowego. W ogólnym przypadku, zależność sygnału wyjściowego od wejściowego, czyli funkcja przejścia (transmitancja), może przyjmować dowolnie skomplikowaną postać w zależności od konstrukcji układu.

Nie dość, że jest ona trudna do wyznaczenia, to jest zupełnie bezużyteczna w praktycznej ocenie liniowości układu (nie mówiąc już o porównaniu różnych rozwiązań układowych) ze względu na wymagany wysiłek obliczeniowy. Bazowanie na funkcji przejścia przy specyfikacji gotowych produktów i odnoszenie się do niej w kartach katalogowych zupełnie mijałoby się z celem. W praktyce potrzebne jest spójne kryterium porównawcze dla dowolnych układów przeznaczonych do danej aplikacji.

Punkt przechwytu n-tego rzędu

Definicja punktu przechwytu n-tego rzędu (IPn) bazuje na rozwinięciu funkcji przejścia układu w szereg Taylora:
y = A₀ + A₁x + A₂x² + A₃x³ + ... + A_nxⁿ

Rys. 2. Punkt przechwytu 3. rzędu i punkt kompresji 1 dB

Współczynnik A₀ nie zmienia kształtu sygnału, wprowadza jedynie przesunięcie o stałą wartość. Pierwszy wyraz A₁x to funkcja liniowa, gdzie A₁ odpowiada wzmocnieniu układu. Pozostałe wyrazy A_nxⁿ reprezentują kolejno nieliniowości od 2. do n-tego rzędu. Ze względu na występujący w technice radiowej szeroki zakres wzmocnień wygodnie jest używać skali logarytmicznej do prezentacji zależności sygnałów, przy czym częściej porównuje się moce sygnałów, wyrażone zwykle w decybelach w odniesieniu do 1 mW (dBm).

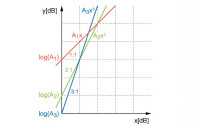
Z takiego podejścia wynika też pewna korzyść. Jak pokazuje rysunek 1, prezentacja każdego z wyrazów szeregu Taylora A_nxⁿ jako funkcji y(x) w skali logarytmicznej to linia prosta o nachyleniu równym n, przecinająca oś y w punkcie log(A_n). Tym samym analiza pozornie skomplikowanego zagadnienia sprowadza się do zbadania wzajemnego położenia w układzie współrzędnych kilku prostych o znanym nachyleniu.

Nietrudno zauważyć, że niezależnie od tego, jak małe byłyby wartości współczynników dla wyrazów wyższych rzędów, zawsze będzie istniała taka wartość sygnału wejściowego, dla której prosta wyższego rzędu przetnie prostą związaną z wyrazem liniowym. To przecięcie prostej A_nxⁿ z prostą A₁x wyznacza właśnie punkt przechwytu n-tego rzędu, czyli IPn. Współrzędne tego punktu, odpowiadające wartościom mocy sygnałów na wejściu i wyjściu, nazywane są odpowiednio OIPn i IIPn (Output IPn, Input IPn).

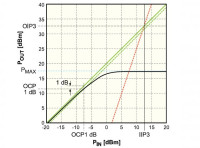
Powyżej punktu IPn składowa sygnału wyjściowego pochodząca od wyrazu nieliniowego n-tego rzędu byłaby większa od składowej związanej z wyrazem liniowym. Oznacza to, że dla wyższych wartości sygnału wejściowego zachowanie układu byłoby zdeterminowane przez wyraz nieliniowy. W rzeczywistych układach jednak znacznie wcześniej niż dojdzie do osiągnięcia któregokolwiek punktu przechwytu następuje nasycenie wyjścia układu (rys. 2).

Rys. 3. Filtracja zniekształceń harmonicznych

Punkt przechwytu jest, jak widać, parametrem poniekąd "wirtualnym", znajdującym się poza obszarem pracy urządzenia. Pomimo to, ma on duże znaczenie praktyczne wynikające z faktu, że IPn określa jednoznacznie położenie prostej n-tego rzędu w zakresie normalnej pracy układu. Daje to dokładną informację na temat mocy niepożądanych komponentów na wyjściu, wynikających z nieliniowości n-tego rzędu, występujących przy określonej mocy sygnału wejściowego.

Ze względu na fakt, że położenie prostej A₁x wynika tylko ze wzmocnienia, często podaje się dla wygody tylko jedną współrzędną punktu IPn w zależności od typu układu. Drugą można wyznaczyć z prostej zależności OIPn_dBm = G_dBm + IIPn_dBm. W przypadku nadajników i wzmacniaczy z reguły punkt przechwytu odniesiony jest do wyjścia (OIPn), zaś odbiorniki charakteryzowane są częściej w odniesieniu do wejścia (IIPn).

Na rysunku 2 oznaczono również parametr opisujący umowną granicę obszaru liniowego. Jest to punkt kompresji jednodecybelowej (compression point 1 dB, CP 1 dB), określający poziom mocy, przy którym następuje spadek rzeczywistego wzmocnienia o 1 dB względem prostej A₁x. Pomiędzy IP3 i CP 1 dB nie ma bezpośredniego związku, gdyż IP3 to efekt wartości A₁ i A₃ wielomianu Taylora, a CP 1 dB wynika z rzeczywistej funkcji przejścia i warunków nasycenia wyjścia.

Z reguły potwierdza się empiryczna reguła OIP3 = OCP 1 dB + (8 ... 12 dB), przy czym różnica między tymi parametrami jest większa w przypadku nowoczesnych ultraliniowych wzmacniaczy niskoszumowych. Podobnie jak w przypadku IP3, CP 1 dB jest odniesiony do wejścia lub wyjścia.

Dlaczego IP3?

Rys. 4. Zniekształcenia intermodulacyjne 2. i 3. rzędu

W telekomunikacji jednym z głównych zagadnień jest przetwarzanie sygnału zmodulowanego, czyli takiego, który niezależnie od typu modulacji jest związany z jakąś częstotliwością nośną i przyległymi do niej pasmami (wstęgami bocznymi) niosącymi informację o sygnale użytkowym. Podstawowym sygnałem testowym jest tutaj sygnał sinusoidalny. Gdyby układ był idealnie liniowy, widmo sygnału wyjściowego zawierałoby tylko częstotliwość sygnału wejściowego.

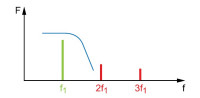
W obecności nieliniowości n-tego rzędu sygnał wyjściowy będzie zawierał składowe o częstotliwościach harmonicznych sygnału wejściowego. Pojawienie się w sygnale wyjściowym częstotliwości, których nie było w sygnale wyjściowym, w przypadku układów wzmacniających jest zawsze niepożądane. W przypadku, gdy sygnał wejściowy zawiera tylko jedną częstotliwość, dosyć łatwo sobie z tym poradzić, ponieważ częstotliwości harmoniczne są na tyle oddalone od podstawowej, że wystarczy zastosowanie prostego filtru dolnoprzepustowego (rys. 3).

Sytuacja komplikuje się, gdy na wejście podamy sygnał testowy będący sumą dwóch lub więcej przebiegów sinusoidalnych o różniących się częstotliwościach. Rozpatrując nieliniowość n-tego rzędu, mamy do czynienia z podnoszeniem sumy dwóch przebiegów do n-tej potęgi, co powoduje powstanie nie tylko częstotliwości harmonicznych, ale również częstotliwości będącymi liniowymi kombinacjami częstotliwości podanych na wejście.

Opisuje je ogólna zależność k_IMn = k₁f₁ + k₂f₂ + ... + k_nf_n, gdzie k_n może przyjmować dowolne wartości całkowite (dodatnie i ujemne), a f_n to kolejne częstotliwości podstawowe podane na wejście. Te nadmiarowe częstotliwości niebędące harmonicznymi sygnałów wejściowych noszą nazwę zniekształceń intermodulacyjnych. Suma wartości bezwzględnych współczynników O = |k₁| + |k₂| + |k₃| +...+ |k_n| określa rząd zniekształceń.

Rysunek 4 ilustruje zniekształcenia intermodulacyjne generowane przez nieliniowości drugiego i trzeciego rzędu w przypadku sygnału wejściowego złożonego z dwóch częstotliwości (sygnał dwutonowy). Wyraz drugiego rzędu przyjmuje wtedy postać A₂(x₁ + x₂)² = A₂(x₁² + x₂² + 2x₁x₂). Dwa pierwsze wyrazy powodują powstanie zniekształceń harmonicznych 2f₁ i 2f₂, natomiast ostatni iloczyn sygnałów x₁ i x₂ to nic innego jak przemiana częstotliwości, odpowiedzialna za powstanie składowych o częstotliwościach |f₁-f₂| i f₁+f₂, czyli zniekształceń intermodulacyjnych 2. rzędu. Poza specyficznymi zastosowaniami, nie stanowią one problemu większego niż zniekształcenia harmoniczne ze względu na możliwość łatwej filtracji.

Rozpatrując analogicznie wyraz trzeciego rzędu, otrzymujemy A₃(x₁ + x₂)³ = A₃ (x₁³ + x₂³ + 3x₁2x₂ + 3x₁x₂²). Dwa pierwsze wyrazy znowu generują harmoniczne, tym razem 3f₁ i 3f₂. Pozostałe wyrazy powodują powstanie nieco ciekawszych kombinacji: 2f₁ + f₂, 2f₁ - f₂, f₁ + 2f₂ oraz i 2f₁ - f₂, stanowiących zniekształcenia intermodulacyjne trzeciego rzędu.

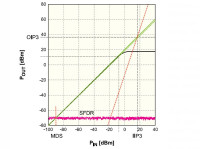
Rys. 5. Graficzna zależność szerokości bezzakłóceniowego zakresu dynamicznego SFDR od punktu przechwytu IP3

O ile składowe 2f₁ + f₂ i f₁ + 2f₂ ciągle podlegają łatwej filtracji, o tyle pozostałe dwie mają bardzo przykrą cechę - im mniejsza różnica między częstotliwościami podstawowymi podawanymi na wejście, tym bliżej tych częstotliwości znajdą się składowe intermodulacyjne. Eliminacja tych składowych staje się trudna nawet z użyciem skomplikowanych filtrów.

Co więcej, często nie można nawet próbować ich usunąć, gdyż pojawiają się one wewnątrz pasma zajmowanego przez sygnał zmodulowany. Minimalizacja zniekształceń intermodulacyjnych powodowanych przez nieliniowość 3. rzędu, którą opisuje punkt IP3, jest zatem kluczowa dla prawidłowej obróbki sygnału użytkowego.

Podobna analiza przeprowadzona dla kolejnych wyrazów szeregu Taylora wykazuje, że nieliniowości nieparzystych rzędów są bardziej uciążliwe od parzystych. Ponieważ moc składowych wynikających z nieliniowości wyższych rzędów maleje ze wzrostem rzędu, schodząc stopniowo poniżej poziomu szumu, rzadko analizuje się zniekształcenia rzędów wyższych niż piąty.