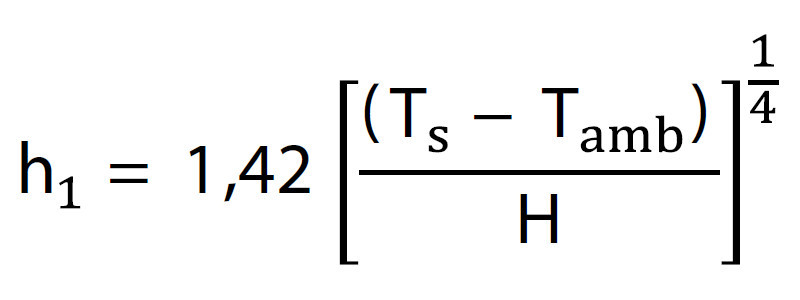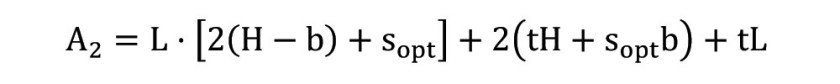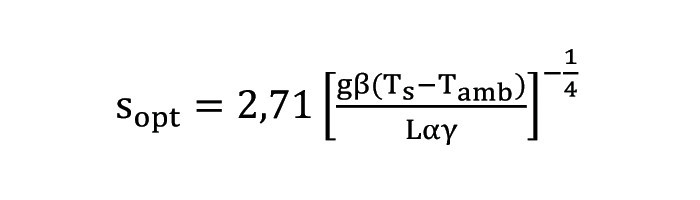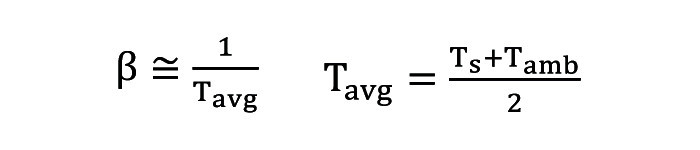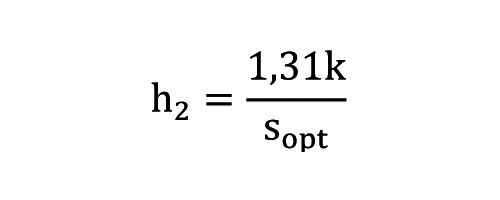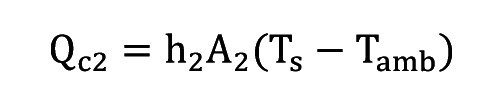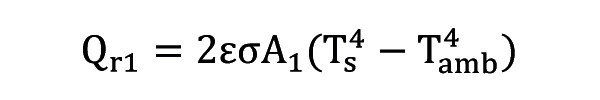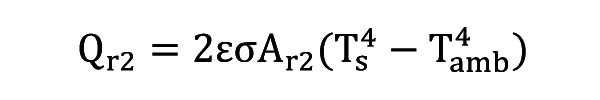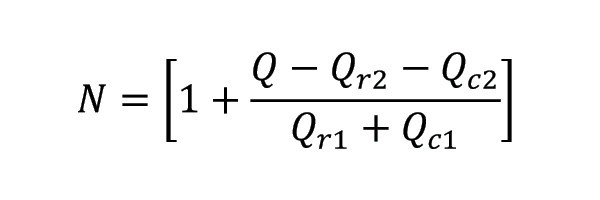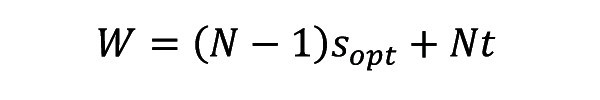Obliczanie wymiarów radiatora w systemie chłodzenia pasywnego

Szacowanie wymiarów radiatora opiera się na kilku równaniach oraz zasadach fizycznych, związanych z termodynamiką oraz mechanizmami rozchodzenia się i wymiany energii cieplnej w otoczeniu. Realizacja tego zadania możliwa jest nawet bez użycia specjalistycznych narzędzi i kalkulatorów, wymaga jednak przyjęcia pewnych założeń i uproszczeń. Znajomość tego zagadnienia niewątpliwie pogłębi wiedzę każdego konstruktora obwodów elektronicznych oraz zwiększy świadomość w zakresie zarządzania temperaturą układu i projektowania systemów chłodzenia.

Założenia początkowe

 

Rys. 1. Poszczególne wymiary radiatora żeberkowego

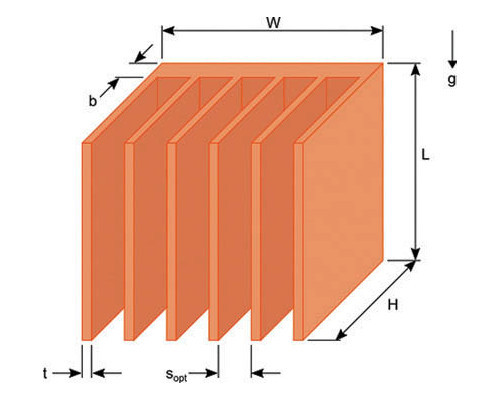
Efektem końcowych przeprowadzonych obliczeń powinny być wartości odpowiadające poszczególnym wymiarom radiatora. W tekście przyjęto, że obliczenia prowadzone są dla radiatora o konstrukcji żeberkowej, takiego jak na rysunku 1. Tego typu elementy spotykane są powszechnie w systemach pasywnego chłodzenia komponentów elektronicznych. Rysunek przedstawia sześć różnych wymiarów, wymaganych do pełnego opisu radiatora. W celu uproszczenia dalszych obliczeń przyjąć można następujące założenia:

• Wymiary b oraz t są znacznie mniejsze niż L, W i H, przez co pole powierzchni prostopadłe do kierunku przepływu strumienia powietrza g jest pomijalnie małe w stosunku do całej powierzchni radiatora.
• Przewodnictwo cieplne materiału, z którego zbudowany jest radiator, jest na tyle duże, że rozkład temperatury na całej powierzchni tego elementu jest jednorodny i w przybliżeniu równy temperaturze źródła ciepła.
• Źródło ciepła ma takie same wymiary, co podstawa radiatora, narzuca zatem wartość parametrów L oraz H.
• Połączenie pomiędzy źródłem ciepła oraz radiatorem jest idealne, tzn. pozwala na natychmiastowy oraz bezstratny transfer energii cieplnej.

Powyższe założenia powodują, że końcowy wynik obliczeń obarczony jest pewnym błędem. Jego wartość w znakomitej większości przypadków powinna być jednak na tyle nieistotna, aby możliwe było wykorzystanie otrzymanych rezultatów do celów szacunkowych.

Dalsza analiza zakłada również, że podstawa radiatora zorientowana jest pionowo, zaś chłodzenie odbywa się za pomocą procesu naturalnej konwekcji i promieniowania, bez wymuszonego obiegu powietrza w układzie oraz przy pomijalnym wpływie odprowadzania ciepła z komponentu przez przewodnictwo.

Obliczenie wpływu konwekcji

 

Rys. 2. Obszary wykorzystywane do prowadzenia obliczeń tempa wymiany energii cieplnej

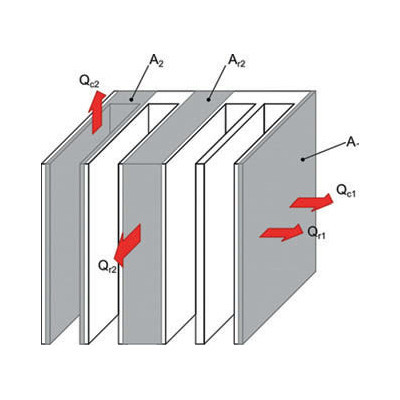
Jak wynika z przyjętych założeń, wartości L oraz H narzucone są z góry przez wymiary źródła ciepła. Do obliczenia pozostaje zatem wartość W, czyli szerokość radiatora, odległość pomiędzy żebrami (s) oraz liczba żeber N. Na rysunku 2 przedstawiono obszary, dla których obliczone zostanie tempo wymieniany energii cieplnej w procesach konwekcji oraz promieniowania. Moc rozpraszana w wyniku konwekcji z obszaru QC1 może zostać opisana za pomocą równania:

Q_c1 = 2h₁A₁ (T_s − T_amb)

gdzie: T_S – temperatura źródła ciepła, T_amb – temperatura otoczenia, h₁ – współczynnik wnikania ciepła dla obszaru A₁. Pole powierzchni A₁ obliczyć można przez znajomość poszczególnych wymiarów radiatora:

A₁ = HL + t(2H + L)

Współczynnik wnikania ciepła wynosi:

Wzór ten jest prawidłowy dla procesu naturalnej konwekcji z pionowo zorientowanej powierzchni. Następny krok polega na obliczeniu mocy rozpraszanej w wyniku konwekcji w obszarze A₂, czyli obszarze obejmującym wszystkie żebra. Do obliczenia pola powierzchni A₂ wykorzystać można równanie:

Optymalna wartość odległości pomiędzy żebrami, pozwalająca na osiągnięcie największego tempa transferu energii cieplnej w przypadku naturalnej konwekcji, to:

gdzie: g – przyspieszenie ziemskie, β – współczynnik rozszerzalności cieplnej, w przybliżeniu

α – współczynnik wyrównania temperatur (dyfuzyjność termiczna) powietrza dla temperatury T_avg, γ – lepkość kinetyczna powietrza dla temperatury T_avg. Dla obszaru żeber współczynnik wnikania ciepła to:

gdzie k to współczynnik przewodnictwa cieplnego dla powietrza w temperaturze T_avg. Ciepło rozpraszane w obszarze A₂ opisać można za pomocą:

Podobnie jak w przypadku obszaru A₁, pojedyncza wartość współczynnika wnikania ciepła dla całego obszaru jest akceptowalna ze względu na niewielkie różnice wartości tego współczynnika dla powierzchni o różnej orientacji, a także na nieduży udział tych powierzchni w całkowitym procesie oddawania ciepła, wynikający z ich niewielkiego pola powierzchni.

Obliczanie wpływu promieniowania

Wpływ zjawiska promieniowania na całkowitą wartość rozpraszania ciepła przez radiator może być dość znaczny, szczególnie w przypadku chłodzenia pasywnego. Efekt ten powinien zatem zostać uwzględniony w analizie całkowitej efektywności radiatora. Podobnie jak w przypadku wymiany ciepła poprzez konwekcję, radiator podzielić można na dwa obszary – podstawę oraz ożebrowanie. Moc ciepła rozpraszanego w wyniku promieniowania z obszaru podstawy to:

gdzie ε to tzw. zdolność emisyjna powierzchni radiatora, zaś σ to stała Boltzmanna, o wartości 5,67·10^–8W/ m²K⁴.

Moc promieniowania cieplnego pochodzącego z obszaru żeber radiatora określana jest za pomocą:

Dokładne obliczenie poziomu promieniowanej mocy cieplnej z obszaru A₂ jest dość skomplikowane, ale dobrym przybliżeniem jest jednak wykorzystanie pozornej powierzchni promieniowania, składającej się z zewnętrznych granic obszaru A₂:

Obliczenie rozmiarów radiatora

Ostatecznym krokiem procesu analizy jest obliczenie liczby żeber N niezbędnej do rozproszenia ciepła produkowanego przez źródło ciepła o temperaturze T_s

Znajomość liczby żeber pozwala następnie na obliczenie szerokości radiatora:

Podsumowanie

Przedstawione w tekście obliczenia pozwalają w uproszczony sposób wyznaczyć rozmiary radiatora wymaganego do skutecznego odprowadzenia ciepła z urządzenia o określonej temperaturze, pracującego w znanej temperaturze otoczenia i są wykorzystywane w dostępnych w Internecie kalkulatorach. Niemniej równania te pozwalają również uświadomić sobie wpływ poszczególnych parametrów radiatora oraz jego otoczenia na ostateczną efektywność pracy systemu chłodzenia (funkcja edukacyjna). Bardziej precyzyjna analiza właściwości termicznych wymaga wykorzystania zaawansowanych narzędzi symulacyjnych oraz specjalistycznego oprogramowania.

Damian Tomaszewski