Żyroskopy MEMS w trudnych warunkach środowiskowych

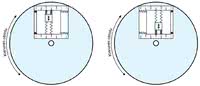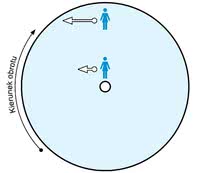
Rys. 1. Przykład obrazujący powstawanie efektu Coriolisa. Osoba poruszająca się wzdłuż promienia obracającego się dysku, chcąc poruszać się po linii prostej, musi zmieniać swoją prędkość liniową (symbolizowaną przez długość strzałki).

Większość konstruktorów sądzi pewnie, że zastosowanie żyroskopów ogranicza się głównie do urządzeń elektroniki popularnej, pracujących w normalnych warunkach środowiskowych. To prawda, że temperatura pracy większości dostępnych układów mieści się w zakresie od -40 do ok. 85°C. Od pewnego czasu na rynku dostępne są jednak również układy mogące pracować w temperaturze do 175°C, odporne na silne wstrząsy (do 1000 g) oraz wibracje.

Większość żyroskopów wykonywanych w technologii MEMS wykorzystuje działanie efektu Coriolisa. Przyczyny powstawania tego zjawiska obrazuje rysunek 1. Jeśli obiekt porusza się wzdłuż promienia obracającego się ciała, odczuwa przyspieszenie związane ze zmianą swojej prędkości liniowej. Wartość tego przyspieszenia zależy od prędkości obrotowej ciała - im szybciej się obraca, tym większa siła działa na poruszający się po nim obiekt.

Zjawisko to powoduje zakrzywienie toru ruchu obiektu. Gdyby obiekt chciał poruszać się wzdłuż promienia obracającego się ciała po linii prostej, musiałby tak zmieniać swoją prędkość liniową, by przeciwstawić się działaniu siły Coriolisa (na rysunku wartość tej prędkości symbolizowana jest przez długość niebieskiej strzałki).

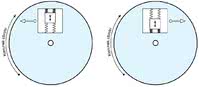
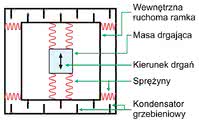
Rys. 2. Na poruszającą się po promieniu wirującego dysku masę oddziałuje siła wynikająca z działania efektu Coriolisa. Zwrot i kierunek tej siły w zależności od położenia masy pokazuje strzałka

W żyroskopie MEMS funkcję poruszającego się obiektu pełni poruszająca się masa przymocowana do zewnętrznej ramki, tak jak pokazano na rysunku 2. Masa porusza się ruchem drgającym, co powoduje powstawanie siły Coriolisa. Zgodnie z zasadą akcji i reakcji, powstaje oddziałująca na ramkę siła przeciwna do siły Coriolisa.

Jak pokazano na rysunku, gdy masa porusza się w kierunku zewnętrznej krawędzi, na ramkę oddziałuje siła skierowana w lewo. W przypadku ruchu masy w stronę centrum okręgu, na ramkę oddziałuje siła skierowana w prawo (zwrot i kierunek siły działającej na ramkę pokazuje na rysunku pomarańczowa strzałka).

Rys. 3. Mechaniczna budowa żyroskopu MEMS

Wartość siły oddziałującej na ramkę jest proporcjonalna do prędkości obrotowej ciała. By zmierzyć tę siłę, ramka umocowana jest do podłoża za pomocą sprężyn, ma więc możliwość ruchu w kierunku prostopadłym do kierunku drgań masy, tak jak pokazano na rysunku 3. Przesunięcie ramki mierzone jest za pomocą kondensatora grzebieniowego - zmiana wzajemnego położenia okładek kondensatora powoduje zmianę jego pojemności.

Ogólną zasadę działania żyroskopu MEMS przedstawiono na rysunku 4. Drgania masy powodują na skutek występowania ruchu obrotowego powstanie siły działającej na ruchomą ramkę, w efekcie czego następuje przesunięcie ramki w kierunku prostopadłym do drgań masy. Przesunięcie to powoduje zmianę pojemności kondensatora grzebieniowego. Gdy ciało się nie obraca, ramka pozostaje nieruchoma, a pojemność kondensatora jest stała.

Pomiar pojemności

Rys. 4. Zmiana położenia ramki podczas ruchu masy drgającej (przy obecności ruchu obrotowego)

W praktyce okazuje się, że powstająca wskutek działania efektu Coriolisa siła jest skrajnie mała - powoduje wzajemne przesunięcie okładek kondensatora o odległość z zakresu ułamków A (1 angstrem = 10-10 m), wywołując zmiany pojemności rzędu zF (1 zeptofarad = 10-21 F).

W takim przypadku konieczne jest szczególnie staranne zminimalizowanie wpływu na dokładność pomiaru różnych czynników zakłócających, takich jak temperatura, szum elektryczny czy drgania obudowy.

Osiąga się to m.in. poprzez umieszczenie układów elektronicznych, takich jak wzmacniacze i filtry, na jednym podłożu krzemowym razem z elementami mechanicznymi. Dodatkowo, tor sygnałowy projektuje się głównie w oparciu o sygnał różnicowy. Przy obliczaniu sygnału wyjściowego bardzo ważne jest także uwzględnienie efektów związanych z ruchem drgającym masy.

Wpływ czynników zewnętrznych na dokładność żyroskopu

Teoretycznie sygnał na wyjściu żyroskopu powinien zależeć jedynie od wartości prędkości obrotowej, jednak w praktyce wszystkie tego typu układy wykazują pewną wrażliwość na występowanie przyspieszenia liniowego oraz wibracji, spowodowaną m.in. skończoną dokładnością wykonania elementów mechanicznych.

Podatność na tego typu zakłócenia określają parametry g-sensitivity oraz g²-sensitivity (patrz ramka), które mają znaczący wpływ na całkowitą dokładność czujnika. Niektóre urządzenia wykazują również szczególną wrażliwość na uderzenia - wystawione, nawet przez bardzo krótki czas, na działanie przyspieszenia o znacznej wartości (rzędu kilku setek g), potrafią zablokować się.

Przestają wtedy dokonywać pomiarów - sygnał na wyjściu, niezależnie od prędkości obrotowej ciała, pozostaje stały. W takiej sytuacji, w celu przywrócenia poprawnej pracy, konieczne jest ponowne uruchomienie urządzenia.

Przykład żyroskopu do pracy w trudnych warunkach środowiskowych

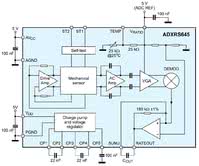
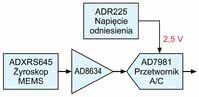
Rys. 5. Schemat blokowy układu ADXRS645. Wyróżnić można dwa główne obwody: zarządzający ruchem masy drgającej oraz odpowiedzialny za przetwarzanie sygnału różnicowego

Pierwszy żyroskop MEMS przystosowany do pracy w wysokiej temperaturze (do 175°C) to ADXRS645 opracowany przez Analog Devices. Urządzenie jest także odporne na wstrząsy do wartości 1000 g. W układzie funkcję elementu pomiarowego pełnią cztery niezależne rezonatory (ruchome ramki wraz z masą drgającą), pracujące parami w przeciwfazie.

Wykorzystanie pochodzącego od nich sygnału różnicowego pozwoliło wyeliminować wpływ zakłóceń związanych z odziaływaniem zewnętrznych przyspieszeń oraz wibracji. Uproszczony schemat blokowy urządzenia przedstawiono na rysunku 5.

Praktyczne wykorzystanie

Rys. 6. Tor pomiarowy do pracy w temperaturze do 175°C

Żyroskopy MEMS zdolne do pracy w wysokich temperaturach znajdują zastosowanie w tak wymagających dla układów elektronicznych dziedzinach, jak choćby górnictwo naftowo-gazowe. Zastępują tam magnetometry, używane wcześniej do kontrolowania prędkości obrotowej ostrzy wiertniczych.

W przeciwieństwie do tych drugich, charakteryzują się niewrażliwością na zakłócenia związane z pracą w pobliżu materiałów ferromagnetycznych. Dodatkowo, umożliwiają bezpośredni pomiar prędkości obrotowej - bez potrzeby stosowania dodatkowych algorytmów przetwarzania danych.

Przykładowy uproszczony schemat toru pomiarowego dla żyroskopu MEMS, pracującego w temperaturze do 175°C, przedstawiono na rysunku 6. Składa się on ze wspomnianego już żyroskopu z wyjściem analogowym (ADXRS645), wzmacniacza operacyjnego (AD8634) oraz przetwornika A/C (AD7981) wraz ze źródłem napięcia odniesienia (ADR225).

Damian Tomaszewski