Sztuczna inteligencja - teoria i praktyka

Początek historii sztucznej inteligencji jest datowany na 1950 rok. Wtedy Alan Turing w artykule zatytułowanym „Computing machinery and intelligence” postawił pytanie „Czy maszyny mogą myśleć?” i opracował test Turinga (imitation game), który pozwala na sprawdzenie zdolności maszyny do naśladowania ludzkiego sposobu rozumowania. Podczas tego badania testujący porównuje ze sobą odpowiedzi na pytania stawiane człowiekowi i maszynie, nie wiedząc z góry, kto ich udziela. Maszyna przechodzi test z wynikiem pozytywnym, jeżeli odpytujący nie jest w stanie stwierdzić, który z odpytywanych jest człowiekiem.

Kolejnym krokiem milowym było użycie terminu „sztuczna inteligencja” po raz pierwszy. Nastąpiło to w 1956 roku, podczas konferencji w Dartmouth College w New Hampshire. Naukowcy biorący w niej udział stwierdzili, że maszyny mogą symulować uczenie się i inne cechy ludzkiej inteligencji, a jeden z nich, John McCarthy, określił AI jako naukę i inżynierię tworzenia inteligentnych maszyn. Spotkanie to oraz wnioski z niego płynące zainspirowały kolejne pokolenia naukowców do prac w tym kierunku.

 

Rys. 1. Klasyfikacja sztucznej inteligencji

Historia i...

W 1966 roku opracowano pierwszego chatbota, czyli program komputerowy do przetwarzania języka naturalnego, naśladujący człowieka podczas rozmowy z ludźmi. Aplikacje Eliza została napisana w MIT AI Laboratory i symulowała zachowanie psychoanalityka. Podobno jej twórcy byli zaskoczeni tym, jak łatwo było stworzyć takie złudzenie.

W latach 70. i 80. zeszłego stulecia pojawiły się systemy ekspertowe, które uważane są za jedną z pierwszych udanych form prymitywnej sztucznej inteligencji. Opierały się na bazach, w których wiedzę ekspertów zapisano w postaci reguł if-then i silnika wnioskowania, który stosował je do nowych danych. Przykładem był MYCIN, medyczny system ekspertowy, który diagnozował choroby.

Nie zawsze jednak zainteresowanie AI było duże. Zmalało przynajmniej dwukrotnie, pierwszy raz w latach 1974–1980 i kolejny, między 1987 a 1993. W obu przypadkach przyczyny były takie same – chodziło o ogromne oczekiwania wobec tej technologii, które nie szły w parze z osiągnięciami.

To zniechęcało naukowców, niemogących pochwalić się wynikami, a w efekcie i inwestorów, którzy wstrzymywali dotacje na ten cel. Nie oznacza to jednak, że w tym czasie w ogóle nie robiono postępów. Przykładowo w 1986 roku opracowano NETtalk, jedną z pierwszych sztucznych sieci neuronowych, modelującą proces uczenia się prawidłowej wymowy, a w 1997 roku komputer Deep Blue pokonał w turnieju szachowym ówczesnego mistrza świata Garriego Kasparowa.

...teraźniejszość

Później przez wiele lat nad AI prowadzono głównie badania akademickie i dopiero około 2011 roku technologia ta szturmem wkroczyła do naszego codziennego życia. Stało się to za sprawą wirtualnych asystentów opartych na algorytmach sztucznej inteligencji. Przykładami takich są: Siri firmy Apple na rynku od 2011 roku, Cortana Microsoft u (2014) i Amazon Echo z usługą głosową Alexa (2015). Ich rozwój był możliwy dzięki postępowi w dziedzinie technologii sprzętowej (procesory, pamięci) i oprogramowania.

W międzyczasie nie brakowało też i spektakularnych prezentacji możliwości AI. Takim był udział Watsona, superkomputera firmy IBM, w teleturnieju, w którym pokonał ludzkich przeciwników (2011) i prezentacja Google Duplex, opartego na sztucznej inteligencji systemu do umawiania spotkań przez telefon (2018). Temu drugiemu udało się zapisać do fryzjera i zarezerwować stolik w restauracji bez wzbudzania wątpliwości u osób z obsługi, z którymi rozmawiał.

Przyszłość – potencjalne aplikacje

Jak pisaliśmy we wstępie obecnie, przeważnie, nie zdając sobie z tego sprawy, już korzystamy z aplikacji i narzędzi opartych na sztucznej inteligencji, m.in. kupując online, w wyszukiwarkach internetowych, tłumaczach online, rozmawiając z konsultantami – chatbotami, w inteligentnych domach, w rozwiązaniach cyberbezpieczeństwa. A to dopiero początek – potencjał AI jest ogromny i to w wielu dziedzinach. Przykładowe jej zastosowania w informatyce to: rozpoznawanie mowy, przetwarzanie obrazu, przetwarzanie języka naturalnego. Ważną gałęzią zastosowań sztucznej inteligencji będą również finanse. Przykładami są: usługi doradztwa finansowego świadczone przez chatboty, znajdowanie wzorców w transakcjach oraz czynnikach rynkowych w ramach pomocy inwestorom. AI może być również przydatna w analizie i prognozowaniu zachowań klientów, wspierając specjalistów marketingu i umożliwiając personalizację obsługi klienta.

W medycynie sztuczna inteligencja będzie pomagać lekarzom w diagnozowaniu pacjentów i opracowywaniu zindywidualizowanych planów leczenia. Dzięki AI ma też szansę zmaleć liczba błędów medycznych. Ważnym sektorem zastosowań sztucznej inteligencji jest poza tym transport: autonomiczne samochody oparte na AI mogą zrewolucjonizować przewóz dóbr, jak i osobowe usługi transportowe.

Sztuczna inteligencja – przegląd rozwiązań

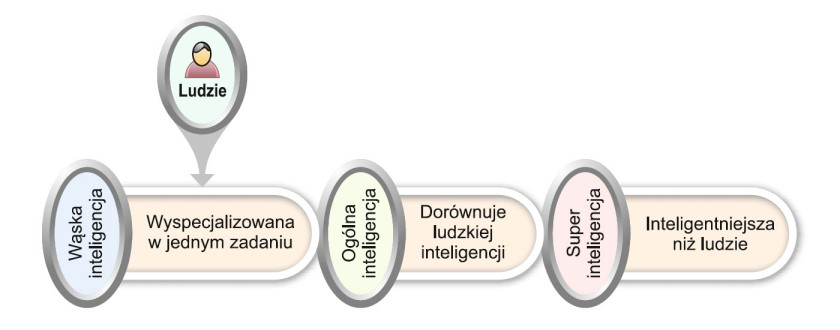
Wyróżnia się kilka typów sztucznej inteligencji, generalnie klasyfikując AI ze względu na jej możliwości. Według pierwszego kryterium rozróżnia się sztuczną inteligencję: wąską (słabą), ogólną i super (silną). Pierwsza, ANI (Artificial Narrow Intelligence), jest wyspecjalizowana wyłącznie w wąskim zagadnieniu i nie może działać poza swoją dziedziną i ograniczeniami. Przykłady aplikacji wąskiej sztucznej inteligencji to: gra w szachy, sugerowanie zakupów w witrynach e-commerce, kierowanie samochodami autonomicznymi, rozpoznawanie mowy i rozpoznawanie obrazów. Ogólna sztuczna inteligencja, GI (Artificial General Intelligence), to z kolei rodzaj AI, który może wykonać każde zadanie wymagające wysiłku intelektualnego na równi z człowiekiem – obecnie nie ma jeszcze tego typu systemów. Podobnie nie opracowano jeszcze superinteligencji, ASI (Artificial Superintelligence). Na tym poziomie maszyny będą już przewyższać ludzi pod względem inteligencji, a każde zadanie będą wykonywać lepiej od człowieka. Będą w stanie tego dokonać dzięki wysoko rozwiniętym właściwościom poznawczym, dziś zarezerwowanym dla nas, jak: zdolność do myślenia, rozwiązywania problemów, dokonywania osądów, planowania, uczenia i komunikowania się samodzielnie.

Obecnie jedyny rodzaj AI w powszechnym użytku to ANI. Słaba sztuczna inteligencja wykorzystuje przeważnie uczenie maszynowe (Machine Learning, ML), którego celem jest zdobywanie umiejętności lub wiedzy z doświadczenia, czyli ich syntezę na podstawie danych historycznych. Wyróżnić w nim można wiele podzbiorów nauk i różnych technik.

Przykładowa klasyfikacja rozróżnia uczenie maszynowe: nadzorowane oraz nienadzorowane. Większość praktycznych implementacji ML wykorzystuje pierwszą technikę. W tej kategorii wyróżnia się dwie grupy zadań: klasyfikację i regresję. W pierwszej zmienną wyjściową jest kategoria, przykładowo: „chory” lub „zdrowy”, „prawidłowy” lub „nieprawidłowy”. Z kolei w regresji jest to liczba rzeczywista. Dalej szerzej opisujemy tę ostatnią technikę.

ML w teorii i w praktyce – czym jest regresja?

Regresja umożliwia znalezienie relacji między zmiennymi. Przykładowe problemy, które pozwala rozwiązać, to określenie zależności: stanu zdrowia pacjentów od ich wieku, masy, nałogów, chorób w rodzinie i zawodu, wynagrodzenia na danym stanowisku od płci, doświadczenia i wykształcenia pracownika, miasta, wielkości firmy, czy ceny domu od jego powierzchni, dzielnicy, odległości od centrum miasta. Dane każdego pacjenta, stanowiska, domu reprezentują jedną obserwację, a na przykład wiek, waga, nałogi, choroby w rodzinie i zawód to cechy wpływające na stan zdrowia.

Powszechną praktyką jest oznaczanie wyjść przez y, a wejść przez x. Dwie lub więcej cech można przedstawić jako wektor x = (x₁, …, x_r), gdzie r jest liczbą wejść. Regresja jest też przydatna, jeśli chcemy prognozować wynik na podstawie nowego zestawu zmiennych. Przykładowo znając taką zależność, można przewidywać zużycie energii elektrycznej w gospodarstwie domowym w ciągu kolejnej godziny na podstawie pory dnia, pory roku, liczby mieszkańców. W miarę jak zwiększa się dostępność danych, regresja znajduje zastosowanie w wielu kolejnych dziedzinach, m.in. w ekonomii i naukach społecznych.

Regresja liniowa

Popularnym algorytmem nadzorowanego uczenia maszynowego jest regresja liniowa. Jej zalety to łatwość implementacji i interpretacji wyników. W regresji liniowej dla wyjścia y i wektora wejść x = (x₁, …, x_r) zakłada się liniową zależność między y i x, opisywaną wzorem: y = β₀ + β₁ x₁ + ... + β_r x_r + ε, gdzie β₀, β₁, …, β_r to współczynniki regresji, z kolei ε to błąd losowy. Celem jest obliczenie estymatorów współczynników regresji b₀, b₁, ...b_r i wyznaczenie funkcji regresji f(x) = b₀ + b₁x₁ + ...+ b_rx_r, charakteryzującej szacowaną zależność pomiędzy danymi wejściowymi i wyjściowymi.

 

Rys. 2. Przykład regresji liniowej

Prognozowana odpowiedź f(x_i) dla każdej obserwacji i = 1 ... n powinna być jak najbardziej zbliżona do rzeczywistej wartości yi, tak aby różnica y_i – f(x_i) była jak najmniejsza. Stopień dopasowania charakteryzuje wartość Σi(y_i – f(x_i))², która dla danych współczynników b₀, b₁, ...b_r powinna być jak najmniejsza. W uczeniu maszynowym złożoność algorytmu zależy od danych wejściowych. Jeśli zmienna wejściowa jest tylko jedna (x = x), mamy do czynienia z najprostszym przypadkiem jednowymiarowej regresji liniowej. Tu warto dodać, że dane wejściowe są dzielone na testowe i treningowe, zwykle w stosunku 25% i 75%. Na podstawie treningowych tworzony jest model. Jeśli jego trafność jest odpowiednio wysoka, sprawdza się go na zestawie testowym. Wyniki te są bardziej wiarygodne, ponieważ na danych tych model wcześniej nie operował.

Regresja liniowa w praktyce

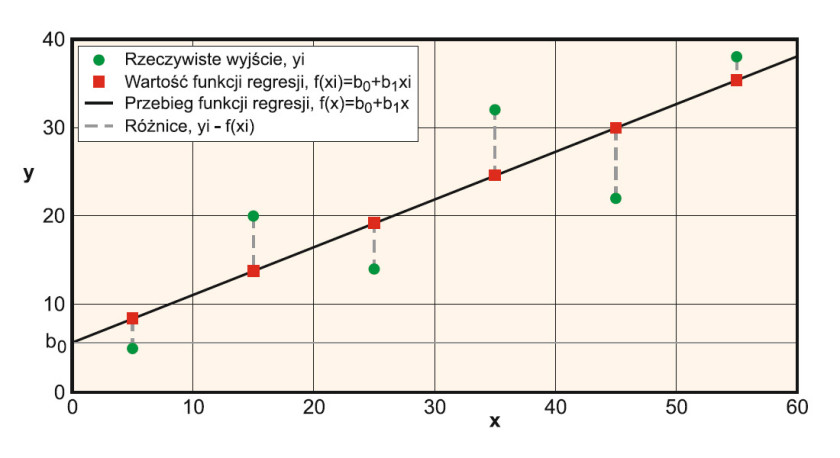
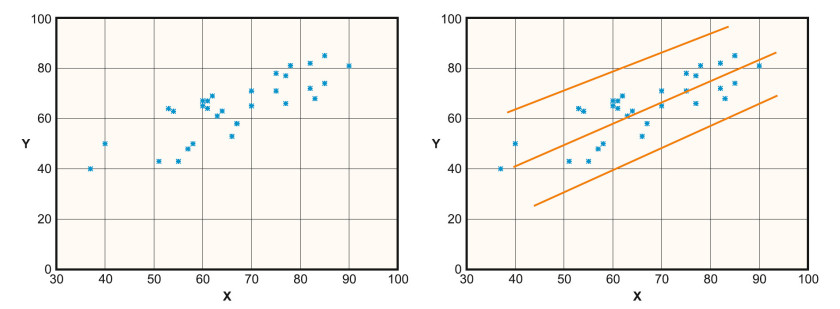
Regresję liniową przedstawia rysunek 2. Punkt wyjścia stanowią pary x – y, oznaczone na rysunku kolorem zielonym. Przebieg szacowanej funkcji regresji pokazuje czarna linia, a opisuje równanie: f(x) = b₀ + b₁x. W punkcie odpowiadającym współczynnikowi b₀ przebieg funkcji regresji przecina oś y – jest to wartość f(x) dla x = 0. Wartość b₁ określa z kolei nachylenie tej prostej. Na czerwono zaznaczono wartości funkcji regresji dla kolejnych wartości wejściowych, a linią przerywaną – różnice między nimi a wartościami rzeczywistymi. Celem jest znalezienie współczynników b₀ i b₁, dla których będą one najmniejsze. Pomocna jest w tym funkcja kosztu. Dzięki niej podejmowana jest decyzja o tym, która linia (rys. 3b) najlepiej opisuje daną zależność (rys. 3a).

 

Rys. 3. a) dane wejściowe, b) szacowane przebiegi funkcji regresji

Funkcja kosztu pozwala ocenić, jak dobrze model, w przypadku regresji liniowej linia, opisuje dane treningowe. Jest wyrażana wzorem: C = Σi(y_i – f(x_i))²/2i, gdzie i to liczba próbek w zbiorze danych treningowych. Im mniejszą wartość ma funkcja kosztu, tym lepszy model. W znalezieniu minimum funkcji kosztu można wykorzystać na przykład metodę gradientu prostego.

Regresja liniowa w Pythonie

Chociaż nie trzeba wiedzieć, jak działa silnik, by prowadzić samochód, to jednak nawet korzystając z bibliotek gotowych funkcji uczenia maszynowego, których udostępnianych jest coraz więcej, dobrze jest znać matematyczne podstawy zaimplementowanych w nich algorytmów. Ułatwia to rozwiązywanie ewentualnych problemów albo dostosowywanie gotowych rozwiązań do własnych potrzeb. Dalej przedstawiamy przykładowy kod uproszczonej implementacji algorytmu regresji liniowej w języku Python bez użycia dedykowanych temu bibliotek.

Z bibliotek można jednak skorzystać na etapie wczytywania i wizualizowania danych – w Internecie można znaleźć wiele tego typu narzędzi. Przykładem jest biblioteka pandas. Za wczytanie danych w przypadku tej biblioteki odpowiada funkcja read. Przykład jej użycia przedstawia poniższy kod:
data = pandas.read _ csv('data.csv').

W celu wizualizacji danych treningowych można skorzystać z biblioteki Matplotlib, a dokładnie z jej interfejsu matplotlib.pyplot. Jest to zbiór funkcji, które pozwalają na rysowanie wykresów w sposób wzorowany na oprogramowaniu Matlab. W celu naniesienia danych treningowych na wykres należy użyć funkcji: scatter, grid, show:
matplotlib.pyplot.scatter(X, Y)
matplotlib.pyplot.grid()
matplotlib.pyplot.show(),
gdzie X i Y to dane treningowe, które rozdzielono na dwie zmienne. Poniżej przedstawiamy kod funkcji kosztu:
def cost _ function (X, Y, b0, b1):
n = len(X)
total _ error = 0.0
for i in range(n): total _ error += (Y[i]–(b0*X[i] – b1))**2
return total _ error/(2*n)
i implementację metody gradientu prostego:
def gradient(X, Y, b0, b1, a):
db0 = 0.0
db1 = 0.0
n = len(X)
for i in range(n):
db0 += -1*X[i]*(Y[i]–(b0*X[i]+b1))
db1 += -1*(Y[i]–(b0*X[i]+b1))
b0 = b0–(1/float(n))*db0*a
b1 = b1–(1/float(n))*db1*a
return b0, b1.

Po kilku iteracjach wartość funkcji kosztu maleje i dobrą praktyką jest jej obserwowanie, ponieważ w pewnym momencie nie zmienia się w ogóle albo już tylko nieznacznie. W kolejnym kroku należy zaimplementować funkcję, która oblicza oraz zwraca wartość y dla danej wartości x, po tym, jak metodą gradientu podstawowego wyznaczone zostaną współczynniki b₀ oraz b₁.
def prediction(x, b0, b1):
return x*b0 + b1.

Na koniec, dla porównania, przedstawiamy również implementację regresji liniowej, ale w popularnej bibliotece funkcji uczenia maszynowego w Pythonie scikit- learn. W tym przypadku zajmuje dwie linijki kodu:
from sklearn.linear _ model import LinearRegression
reg = LinearRegression().fit(X, Y).