Czujniki - generacja sygnałów, ich przetwarzanie i wykorzystywanie

Filtracja oraz próbkowanie

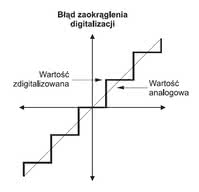
W formowaniu sygnału czujnika inteligentnego bierze udział przede wszystkim filtracja i próbkowanie, będące podstawą jego digitalizacji (rys. 3). Filtracja służy do eliminacji tych wszystkich składowych sygnału, które nie niosą pożądanych informacji, a próbkowanie przetwarza informacje analogowe w formę cyfrową. Najczęściej wykorzystywany jest filtr dolnoprzepustowy.

Pasmo jego przepuszczania wynosi typowo 1500Hz. Filtry dolnoprzepustowe są chyba najczęściej stosowanymi filtrami, gdyż najprostszym sposobem ograniczenia szumów jest stłumienie wszystkich częstotliwości wyższych od granicznej. W przypadku pomiarów temperatury częstotliwość ta jest stosunkowo niska, ogranicza ją bowiem bezwładność termiczna mierzonego ośrodka.

Wszelkie składowe wyższej częstotliwości nie zawierają żadnych informacji temperaturowych. Filtry górnoprzepustowe mają zastosowanie do czujników ze zmiennoprądowym sygnałem, z którego można i należy odfiltrować wszystkie składowe poniżej częstotliwości podstawowej. Na przykład w sygnałach akustycznych przeznaczonych dla ludzkiego ucha wszystkie częstotliwości niższe od 20Hz, dolnej granicy słyszalności, można traktować jako bezużyteczne.

Filtry środkowoprzepustowe do eliminacji wszystkich składowych sygnału poza mieszczącymi się w wybranym paśmie, gdy sygnał użyteczny ma ograniczony zakres częstotliwości, na przykład w czujnikach wibracji, spalania stukowego w silnikach i podobnych. Z kolei filtr środkowozaporowy najczęściej służy do tłumienia zaburzeń wywoływanych częstotliwością sieciową 50Hz lub 60Hz.

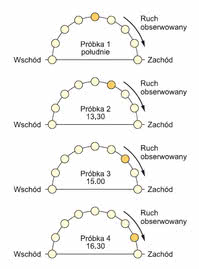
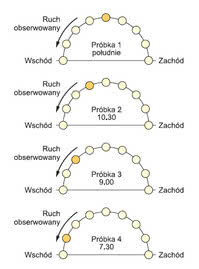
Aliasing Gdy najwyższa składowa częstotliwość sygnału przekracza dwukrotność częstotliwości próbkowania, zwaną częstotliwością Nyquista, składowe powielanych widm nakładają się. Efekt ten, gdy niektóre wyższe składowe jednego widma nie dają się odróżnić od niektórych niższych składowych następnego, wyżej powielonego widma, jest nazywany aliasingiem. Aliasing powinien zostać z systemu wyeliminowany, a zredukowanie jego skutków do pomijalnego poziomu jest możliwe przez wybór dostatecznie dużej szybkości próbkowania. Prostym, ale bardzo widowiskowym przykładem błędów spowodowanych przez aliasing może być próbkowanie pozycji słońca w różnych porach dnia, co jest podstawą czujników zmierzchowych niezawierających zegara RTC i załączających oświetlenie przed wschodem słońca. Na rysunkach przedstawiono pierwszy zbiór pomiarów, dokonywanych co 1,5 godziny. Zgodnie z przewidywaniami pomiary wykazują, że słońce porusza się ze wschodu na zachód. Drugi zbiór pomiarów, dokonywanych co 22,5 godziny, w skutek aliasingu odczytuje się z niego, że słońce porusza się z zachodu na wschód. Jeśli pozycja słońca jest próbkowana co 1,5 godziny, jego obserwowany ruch odbywa się ze wschodu na zachód. Jeśli pozycja słońca jest próbkowana co 22,5 godziny, jego obserwowany ruch ma kierunek odwrotny, z zachodu na wschód. Gdy szybkość próbkowania jest zbyt mała, obserwator odnosi mylne wrażenie.

Filtry cyfrowe

Rys. 4. Błąd digitalizacji sygnału spowodowany zaokrąglaniem

Filtry cyfrowe to algorytmy przetwarzające utworzone przez próbkowanie sygnały cyfrowe. Powstają one przez przypisywanie współczynników wagowych jednemu lub kilku wartościom próbkowanych danych i sumowanie ważonych wartości. Na przykład dla próbkowanego sygnału wejściowego

x_i dla i = 0, 1, 2, ... N-1

można wygenerować przefiltrowany sygnał wyjściowy yi:

y_i = a₀x₀ + a₁x₁ + ... + a_N-1x_N-1

gdzie ai są stałymi współczynnikami ważenia, przyporządkowanymi próbkom sygnału wejściowego xi. Przykładem cyfrowego filtra dolnoprzepustowego jest filtr uśredniający, którego sygnał wyjściowy jest po prostu średnią danej liczby próbek. Sygnał zostaje w ten sposób wygładzony, ponieważ szum jest uśredniany w całej grupie próbek. Jeżeli dla uzyskania przefiltrowanego sygnału wyjściowego do uśrednienia wybiera się cztery próbki, otrzymuje się:

y_i = ¼ x₀ + ¼ x₁ + ¼ x₂ + ¼ x₃

Sygnał wyjściowy filtra może być kształtowany doborem współczynników wagowych dla poszczególnych próbek. Dla ułatwienia projektantom pracy wiele firm oferuje programy do projektowania i analizy filtrów cyfrowych. Darmowe wersje takich programów są dostępne w Internecie. Poprzedni przykład pokazuje strukturę filtra o skończonej odpowiedzi impulsowej (SOI, czyli FIR). Filtry takie zawsze mają skończoną liczbę próbek, zatem ich sygnał wyjściowy zależy jedynie od skończonej liczby próbek wejściowych. Jeśli sygnał wejściowy wprowadza się do filtra o długości N elementów, to sygnał wyjściowy zakończy się po N-tej próbce, ponieważ kolejne próbki wejściowe są już zerowe. Inną strukturę stanowi filtr o nieskończonej odpowiedzi impulsowej (NOI czyli IIR). W tych filtrach ważone są zarówno próbki sygnału wejściowego, jak i sygnału wyjściowego, który przyjmuje postać:

y_i = b₀y_I-1 + b₁y_I-2 + ... b_i-Ky_i-K-1 + a₀x₀ + ... a_N-1x_N-1

gdzie współczynniki bi są stałymi współczynnikami ważenia odpowiednich wyrazów yi-1. Na pierwszy rzut oka ten filtr może się wydać znacznie bardziej skomplikowany, ale tak nie jest. Taką samą funkcję jak poprzednio przytoczonego czteropróbkowego filtra uśredniającego można zrealizować następująco:

y_i = y_i-1 + ¼ x₀ - ¼ x₄

Redukcja wymagań obliczeniowych o jedną próbkę nie jest istotna, znaczne zmniejszenie wymagań obliczeniowych i pamięciowych daje się uzyskać w systemach IIR, jednakże pewnym kosztem. Filtry IIR teoretycznie reagują na sygnały nieskończone (stąd ich nazwa), co nie jest pożądane. Trzeba zadbać, aby błędy się nie kumulowały, gdyż wtedy filtry mogą okazać się bezużyteczne.

Filtry uśredniające (median filters)

Omówione dotąd filtry opisuje się prostymi równaniami matematycznymi, ich działanie daje się więc łatwo analizować znanymi i zrozumiałymi sposobami. Filtry te, odpowiednio projektowane, najlepiej dają się używać do redukcji szumów o specyficznych widmach.

Czasami jednak systemy są podatne na szum zwany śrutowym, w których mierzonemu sygnałowi towarzyszą szumy o charakterze nie ciągłym, lecz wybuchowym. Do przeciwdziałania temu zjawisku stosuje się inny sposób filtracji, zwany filtrowaniem uśredniającym, w pewnym sensie bardziej heurystyczny, ale doskonale redukujący szumy śrutowe.

W filtrze uśredniającym sygnał jest próbkowany tak samo jak w innych filtrach, ale próbki są szeregowane od największych do najmniejszych (lub odwrotnie, nie wpływa to na wynik) i wybierana jest próbka średnia.