Niezawodność podzespołów i urządzeń elektronicznych

Zależności liczbowe i parametry niezawodnościowe

Sporządzenie ilościowego opisu procesu występowania uszkodzeń i niezawodności wyrobów wymaga przyjęcia określonych modeli statystycznych, które powinny także wiązać się ze zjawiskami fizycznymi zachodzącymi podczas użytkowania danych wyrobów.

Badania próbek (badania laboratoryjne) lub dane z eksploatacji wyrobów pozwalają oszacować częstość występowania uszkodzeń jako iloraz liczby uszkodzeń z i liczności próbki n, a więc h = z/n. Niekiedy ten iloraz wyraża się w procentach.

Liczba uszkodzeń zwiększa się z upływem czasu eksploatacji i skumulowana częstość uszkodzeń (1/n, 2/n, 3/n...) wyznacza dystrybuantę trwałości F(t). Przyjmujemy, że dany wyrób może być w jednym z dwu stanów: jest zdatny do poprawnej pracy albo uległ uszkodzeniu i jest niezdatny do prawidłowego funkcjonowania, przeto sumując prawdopodobieństwa, będziemy mieli R(t) + F(t) = 1.

Przechodząc do intensywności uszkodzeń λ, jej oszacowanie na podstawie badań lub eksploatacji możemy otrzymać, odnosząc częstość uszkodzeń do określonego przedziału czasu λ = z/n · 1/Δt = z/n·t. W praktyce dla większości podzespołów elektronicznych podaje się intensywność uszkodzeń jako stosunek liczby uszkodzeń badanych podzespołów na milion roboczogodzin λ = z/106 h albo - co ma miejsce w przypadku wielu elementów i modułów półprzewodnikowych - jako parametr zwany FIT (failures in time) o wartości wynikającej ze stosunku liczby uszkodzeń, które mogą wystąpić w czasie miliarda roboczogodzin tzn. FIT = z/109 h.

Założenie o losowym i stosunkowo rzadkim występowaniu uszkodzeń w trakcie normalnego użytkowania podzespołów i urządzeń elektronicznych pozwala prowadzić badania niezawodności w dość elastyczny sposób. Można przykładowo przyjąć, że intensywność λ = 3×10-6 h, jeśli 3 uszkodzenia zaobserwowano w grupie 100 wyrobów, które pracowały (lub były badane laboratoryjnie) przez 10 000 godzin, albo gdy 3 uszkodzenia zaobserwowano wśród 1000 egzemplarzy wyrobów pracujących w przedziale czasu 1000 godzin.

Wykorzystanie wartości intensywności uszkodzeń λ poszczególnych podzespołów składowych stanowi jedną z metod przewidywania niezawodności zbudowanych z nich urządzeń i systemów elektronicznych. Wartości λ są na ogół podawane przez producentów podzespołów na bazie prowadzonych badań laboratoryjnych.

Należy jednak pamiętać, że dotyczą one określonych warunków badania. W konkretnych zastosowaniach należy wziąć pod uwagę procedury uściślające takie dane bazowe. W procedurach podanych w wojskowych normach amerykańskich MIL-HDBK-217 wylicza się przykładowo końcową wartość λ, posługując się iloczynowym wyrażeniem ze współczynnikami wynikającymi z bliższego określenia typu podzespołu (np. układy scalone analogowe lub cyfrowe, rodzaje kondensatorów, rezystorów, tranzystorów itp.), a dalej warunkami jego pracy i warunkami środowiskowymi, a nawet warunkami techniczno-organizacyjnymi dotyczącymi eksploatacji.

Może to znacząco zmieniać publikowane wartości bazowe λ. Procedury szacowania parametrów niezawodnościowych opracowane zostały także w różnych firmach, głównie amerykańskich, jak np. Telcordia Technical Reference TR-232 Reliability Prediction Procedure for Electronic Equipment, Vicor i in.

Osiągnięcia inżynierii materiałowej i postęp w technologii przyczyniają się do obniżania intensywności uszkodzeń podzespołów. Dla dużej grupy różnorodnych podzespołów można przyjąć, że obserwowane wartości λ nie przekraczają obecnie poziomu 10-6 h, co oznacza, że jedno uszkodzenie występuje przeciętnie w ciągu miliona lub nawet dopiero miliarda roboczogodzin.

Ogólna zależność wiążąca niezawodność z intensywnością uszkodzeń ma postać:

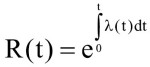
W szczególnym przypadku, przyjmowanym jako dobre przybliżenie rzeczywistej sytuacji w 2. okresie czasowego przebiegu zmian λ, pokazanym na rysunku 1, gdy intensywność uszkodzeń nie zależy od czasu t, możemy przyjąć

Ta wykładnicza zależność jest chętnie i często wykorzystywana w praktyce, ze względu na znaczne ułatwienie ilościowego opisu przy ocenie, przewidywaniu i porównywaniu niezawodności.

Do opisu niezawodnościowych cech wyrobów stosuje się również grupę parametrów związanych z charakterystycznymi wielkościami i zależnościami czasowymi. Można je podzielić na te, które odnoszą się do wyrobów nienaprawialnych i te dotyczące wyrobów naprawialnych. Podzespoły elektroniczne są w zasadzie wyrobami nienaprawialnymi (i w związku z tym nie są naprawiane), podczas gdy urządzenia i systemy elektroniczne są w większości wyrobami naprawialnymi i wobec tego po wystąpieniu uszkodzenia poddaje się je naprawie, w celu przywrócenia do stanu zdatności.

Podstawowym parametrem w przypadku obiektów nienaprawialnych jest średni (przeciętny) czas do wystąpienia uszkodzenia MTTF (mean time to failure). Jest to wartość przeciętna czasu do wystąpienia uszkodzenia danych wyrobów pracujących w określonych warunkach.

Oszacowanie tego czasu wymaga zwykle kontroli znacznej liczby analizowanych wyrobów w stosunkowo długim czasie. Wartość liczbową MTTF uzyskuje się jako iloraz całkowitego czasu pracy analizowanych wyrobów T przez liczbę tych wyrobów N:

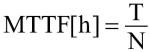
Jeśli można przyjąć założenie o stałej wartości intensywności uszkodzeń, to MTTF jest równe odwrotności intensywności uszkodzeń λ. Zakładając, że intensywność uszkodzeń jest wyrażona w liczbie uszkodzeń na milion godzin, otrzymamy MTTF = 1 000 000/λ godzin. Parametr MTTF można utożsamiać z przeciętną wartością trwałości (czasu życia) wyrobów.

Przykład. Załóżmy, że 10 sztuk wyrobów było badane przez 1 rok i w tym czasie zaobserwowano 2 uszkodzenia po 2500 i 7000 godzinach pracy, a zatem

MTTF = [(8×8 760) + 2500 + 7000] / 10 = 79 080/10 = 7908 h

Co się tyczy obiektów naprawialnych (jak np. złożone moduły, pakiety z obwodami drukowanymi, różnorodne urządzenia i systemy elektroniczne), to za główny parametr niezawodnościowy należy uznać średni (przeciętny) czas między uszkodzeniami MTBF (mean time between failures). Jest to wartość przeciętna czasu między kolejnymi uszkodzeniami podzespołów lub innych elementów składowych danego obiektu. Po wystąpieniu uszkodzenia obiekt jest naprawiany, najczęściej przez wymianę uszkodzonego elementu składowego na nowy. Parametr MTBF oblicza się jako stosunek całkowitego czasu badania (lub eksploatacji) T do liczby uszkodzeń Z

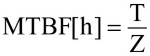
Przykład. Posłużmy się danymi podanymi powyżej, przyjmując, że całkowity czas pracy próbki 10 wyrobów wyniósł 79 080 godzin i że podczas badania zaobserwowano 2 uszkodzenia. Stąd MTBF = 79 080 / 2 = 39 540 h.

Jeśli badania (lub obserwacja pracujących wyrobów) zostałyby przedłużone do 1,5 roku, a w tym czasie nie wystąpiłyby dalsze uszkodzenia, wówczas parametr MTBF byłby równy 57 310 h.

Czasu MTBF nie należy traktować jako minimalny albo gwarantowany czas do uszkodzenia lub między uszkodzeniami, a jego statystyczny charakter nie daje możliwości wykorzystania go do prognozowania niezawodności pojedynczych egzemplarzy wyrobów. Poza tym, czasu MTBF nie można mylić z trwałością (czasem życia) wyrobów - niektóre elementy jak np. baterie mogą mieć czas życia rzędu kilku godzin, a MTBF na poziomie 100 000 h.

Dla modelu z wykładniczym rozkładem czasu życia wyrobów, gdy przyjmuje się, że λ = const, czyli że intensywność uszkodzeń nie zależy od czasu pracy lub badania, MTBF będzie równy odwrotności λ MTBF = 1/ λ.

Natomiast prawdopodobieństwo, że dany wyrób będzie pracował poprawnie przez czas t, wyniesie:

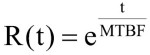
Przykładowo oznacza to, że jeśli dostępne będą dwa rodzaje dysków twardych o MTBF odpowiednio 250 000 godzin (ok. 28,5 roku) i 500 000 godzin (57 lat), wówczas po 5 latach (czyli 43 800 h) eksploatacji prawdopodobieństwo poprawnej pracy tych dysków będzie: I grupa R(t) = 0,839, II grupa R(t) = 0,916. Innymi słowy, można stwierdzić, że wyroby te po 5 latach eksploatacji będą jeszcze pracowały poprawnie z prawdopodobieństwem odpowiednio 83,9% i 91,6% albo że 83,9% (91,6%) tych wyrobów będzie nadal pracowało poprawnie po upływie 5 lat.

Należy mieć na uwadze, że czasy MTBF podawane są przez producentów na podstawie badań lub w oparciu o dane z eksploatacji wyrobów, które pracowały w określonych warunkach na ogół przyjmowanych jako przeciętne, np. w temperaturze otoczenia nieprzekraczającej zwykle 70°C.