Niezawodność podzespołów i urządzeń elektronicznych
| TechnikaPojęcie niezawodności i jego praktyczne znaczenie wiąże się z jakością i przez wiele osób pojęcia te są używane wymiennie, stąd na samym początku trzeba uporządkować terminologię. Jakość określa wewnętrzną doskonałość danego obiektu (wyrobu np. podzespołu, modułu lub urządzenia elektronicznego), pokazując w jakim stopniu spełnia on wymagane funkcje w momencie zakończenia procesu wytwarzania, przekazania do eksploatacji i rozpoczęcia użytkowania. Natomiast niezawodność, zwykle oznaczana jako funkcja R(t), wskazuje jak dany obiekt utrzymuje swoją jakość w czasie i w rzeczywistych warunkach użytkowania, które także mogą ulegać zmianom w czasie. Łącząc oba te pojęcia można powiedzieć, że niezawodność jest jedną z wyróżniających cech jakościowych danego obiektu.
Rozkłady czasu życia wyrobów
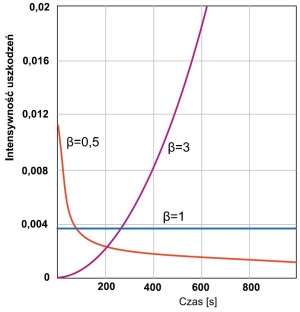
Rys. 2. Gęstość prawdopodobieństwa uszkodzeń w rozkładzie Weibulla w zależności od wartości parametru β
Przyjęcie założenia o niezależności od czasu częstości pojawiania się uszkodzeń pracujących obiektów i akceptacja wykładniczej zależności dla ich niezawodności stanowi - jak to już wspomniano - wygodny model do opisu procesu eksploatacji, zwłaszcza w zasadniczej dla użytkowników fazie tego procesu.
Jednakże gdy zachodzi potrzeba opisu początkowej lub końcowej fazy eksploatacji albo też łącznego potraktowania wyróżnionych faz, a także przy porównawczych ocenach poziomu niezawodności - wówczas przydatne mogą się okazać jeszcze inne (poza wykładniczym) rozkłady trwałości (czasu życia). Warto wśród nich wymienić rozkład logarytmo-normalny i rozkład Weibulla. Aby ocenić przydatność danego rozkładu w konkretnym zastosowaniu, analizuje się teoretyczną funkcję λ(t) wynikającą z rozkładu i porównuje jej przebieg z przebiegiem doświadczalnym.
Zmienna losowa, jaką jest czas życia, ma rozkład logarytmo-normalny, jeśli wartości tego czasu uzyskane z badań lub eksploatacji mają po zlogarytmowaniu (logarytm dziesiętny lub naturalny) rozkład normalny. Rozkład logarytmonormalny może być wykorzystany do opisu trwałości w sytuacji, gdy λ początkowo bardzo szybko narasta (praktycznie od pewnej większej wartości), a następnie maleje w czasie. Odpowiada to przykładowo przebiegowi zaznaczonemu jako okres I w pierwszej części krzywej na rysunku 1.
Ze względu na możliwość zastosowania w wielu praktycznych sytuacjach, dużą popularność uzyskał rozkład Weibulla. Gęstość prawdopodobieństwa w rozkładzie Weibulla ma kształt przedstawiony na rysunku 2 i zależy od 3 parametrów: kształtu β, skali η i parametru początkowego γ. Gdy parametr kształtu β = 1, wówczas rozkład Weibulla przechodzi w rozkład wykładniczy.
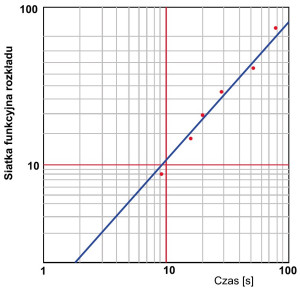
Wykorzystanie rozkładu Weibulla zapewnia dobrą analizę procesu uszkodzeń i przewidywanie niezawodności już na podstawie stosunkowo małych próbek. Praktycznie stosowane są przy tym metody graficzne. Przykładem może być siatka funkcyjna rozkładu (reliability plot), pokazująca zmiany dystrybuanty F(t) = 1 - R(t) w funkcji czasu (rys. 4). Nanosi się na nią dane doświadczalne, co pozwala ocenić zgodność lub odchylenia od linii prostej, odpowiadającej rozkładowi Weibulla.
Przyspieszone badania niezawodności
Rys. 3. Intensywność uszkodzeń w rozkładzie Weibulla w zależności od wartości parametru β
Celem przyspieszonych (forsownych) badań niezawodności wyrobów jest stworzenie takich warunków, które pozwoliłyby na uzyskanie informacji o trwałości w krótszym czasie, niż miałoby to miejsce przy normalnych (typowych) obciążeniach tych wyrobów, związanych z ich określonym zastosowaniem.
Cel ten jest więc różny od tego, który realizuje się podczas wspomnianych wcześniej testów selekcyjnych. W obu jednak przypadkach stosuje się - choć na różne sposoby - obostrzone warunki pracy (badania) wyrobów, podnosząc poziomy obciążeń roboczych i ustalając trudniejsze warunki zewnętrzne (warunki środowiskowe).
W badaniach przyspieszonych doprowadza się do wystąpienia uszkodzeń, aby uzyskać dane o czasie życia wyrobów. Żeby przenieść wyniki w odpowiedniej skali na normalne warunki użytkowania, należy zadbać o zachowanie takich samych mechanizmów uszkodzeń. Często ogranicza to możliwość uzyskania dostatecznie dużych współczynników przyspieszenia.
Czynnikiem powodującym przyspieszenie przebiegu procesów fizykochemicznych prowadzących do wystąpienia uszkodzenia jest niewątpliwie podwyższona temperatura. Zależność współczynnika przyspieszenia od przyrostu temperatury ma charakter wykładniczy i jest znana jako równanie Arrheniusa.
Rys. 4. Przykład siatki funkcyjnej rozkładu Weibulla
Uwzględnienie występujących jednocześnie innych obciążeń, jak np. podwyższony poziom napięć, można przedstawić wykorzystując równanie Eyringa. Opracowane zostały również oddzielne modele ilościowe dla innych czynników, oddziaływających na zmiany szybkości przebiegu procesów prowadzących do wystąpienia uszkodzeń.
Dotyczy to m.in. takiego obciążenia (stresora) jak cykle termiczne, gdzie ilościowy model oddziaływania jest opisywany za pomocą równania Coffina-Mansona. Z kolei efekt łącznego oddziaływania temperatury i wilgoci przedstawia równanie Hallberga-Pecka.
W zależności od przewidywanych zastosowań, w badaniach bierze się również pod uwagę wpływ takich czynników jak wspomniane już poziomy napięć roboczych i prądów, wibracje i wilgotność. Charakterystyczną wielkością odnoszącą się do pobudzenia jakiegoś mechanizmu uszkodzeń jest energia aktywacji danego procesu, której wartość ustala się doświadczalnie dla badanych typów podzespołów.
